Publication and Presentations
For material based upon work supported by the National Science
Foundation, NIH or DARPA
any opinions, findings, and conclusions or recommendations
expressed are those of the author(s) and do not
necessarily reflect the views of the National Science Foundation
or the official views or policies of the Department of Defense
or the U.S. Government.
2025
abstract
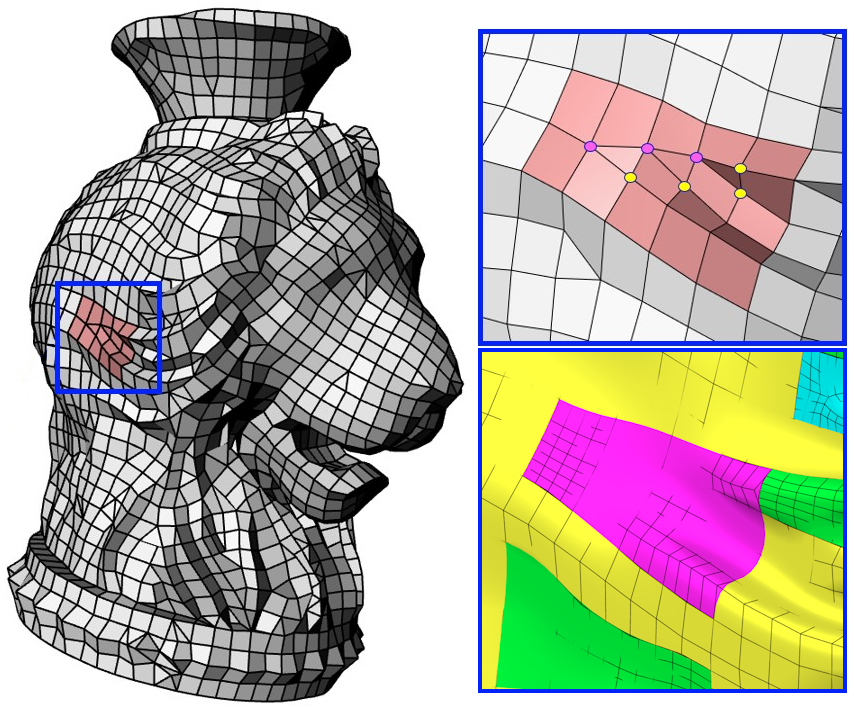
Quad-dominant meshes are popular with animation designers and can efficiently be generated from point clouds. To
join primary regions, quad-dominant meshes include non-4-valent vertices and non-quad regions. To transition between
regions of rich detail and simple shape, quad-dominant meshes commonly use a cascade of n â 1 triangles that reduce
the number of parallel quad strips from n + 1 to 2.
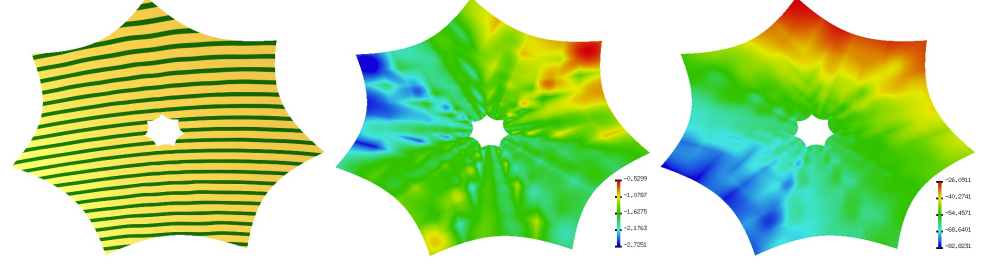
For these cascades, the Narrowing-Cascade spline, short NCn, provides a new shape-optimized G1
spline surface. NCn
can treat cascade meshes as B-spline-like control nets. For n > 3, as opposed to n = 2, 3, cascades have interior points
that both guide and complicate the construction of the output tensor-product NC spline. The NCn spline follows the
input mesh, including interior points, and delivers a high-quality curved surface of low degree.

abstract
On a planar Euclidean domain, Powell-Sabin splines form a rich space of C1 polynomials
of total degree 2, i.e. with constant second derivatives.
However, when the domain has a different structure because the genus of the surface
is not 1, building curved free-form surfaces solely with total degree quadratic polynomials,
with each piece defined over a flat, straight-edge domain triangle, meets with obstructions.
By pinpointing these obstructions, the limitations of modeling with quadratics are made precise,
the allowable C1 free-form constructions are characterized and their
necessary shape-deficiency is demonstrated.
2024
abstract
Classic generalized subdivision, such as Catmull-Clark subdivision, as well as recent subdivision algorithms for high-quality surfaces,
rely on slower convergence towards extraordinary points for mesh nodes surrounded by n > 4 quadrilaterals. Slow convergence
corresponds to a contraction-ratio of λ > 0.5. To improve shape, prevent parameterization discordant with surface growth, or
to improve convergence in isogeometric analysis near extraordinary points, a number of algorithms explicitly adjust λ by altering
refinement rules. However, such tuning of λ has so far led to poorer surface quality, visible as uneven distribution or oscillation of
highlight lines. The recent Quadratic-Attraction Subdivision (QAS) generates high-quality, bounded curvature surfaces based on
a careful choice of quadratic expansion at the central point and, just like Catmull-Clark subdivision, creates the control points of
the next subdivision ring by matrix multiplication. Unfortunately, QAS shares the contraction-ratio λCC > 1/2 of Catmull-Clark
subdivision when n > 4. This shortcoming is finally remedied by the presented improvement QAS+ of QAS. For n = 5, . . . , 10, the
convergence is made a uniform λ = 1/2 as in tensor-product case and without sacrificing surface quality.
abstract
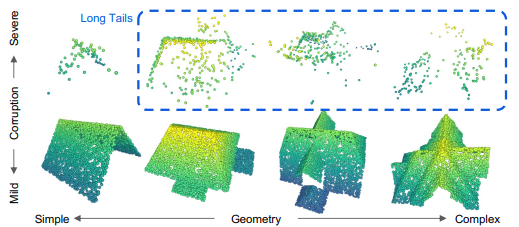
Accurate completion and denoising of roof height maps are
crucial to reconstructing high-quality 3D buildings. Repairing sparse
points can enhance low-cost sensor use and reduce UAV flight over-
lap. RoofDiffusion is a new end-to-end self-supervised diffusion tech-
nique for robustly completing, in particular difficult, roof height maps.
RoofDiffusion leverages widely-available curated footprints and can so
handle up to 99% point sparsity and 80% roof area occlusion (regional
incompleteness). A variant, No-FP RoofDiffusion, simultaneously pre-
dicts building footprints and heights. Both quantitatively outperform
state-of-the-art unguided depth completion and representative inpaint-
ing methods for Digital Elevation Models (DEM), on both a roof-specific
benchmark and the BuildingNet dataset. Qualitative assessments show
the effectiveness of RoofDiffusion for datasets with real-world scans in-
cluding AHN3, Dales3D, and USGS 3DEP LiDAR. Tested with the lead-
ing City3D algorithm, preprocessing height maps with RoofDiffusion no-
ticeably improves 3D building reconstruction. RoofDiffusion is comple-
mented by a new dataset of 13k complex roof geometries, focusing on
long-tail issues in remote sensing; a novel simulation of tree occlusion;
and a wide variety of large-area roof cut-outs for data augmentation and
benchmarking. Code and datase available.

abstract
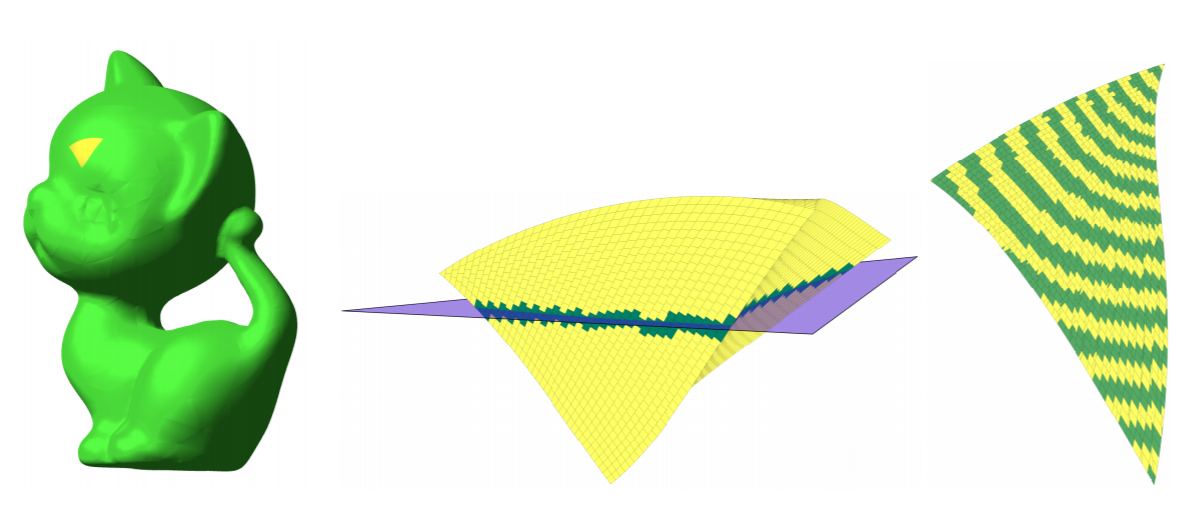
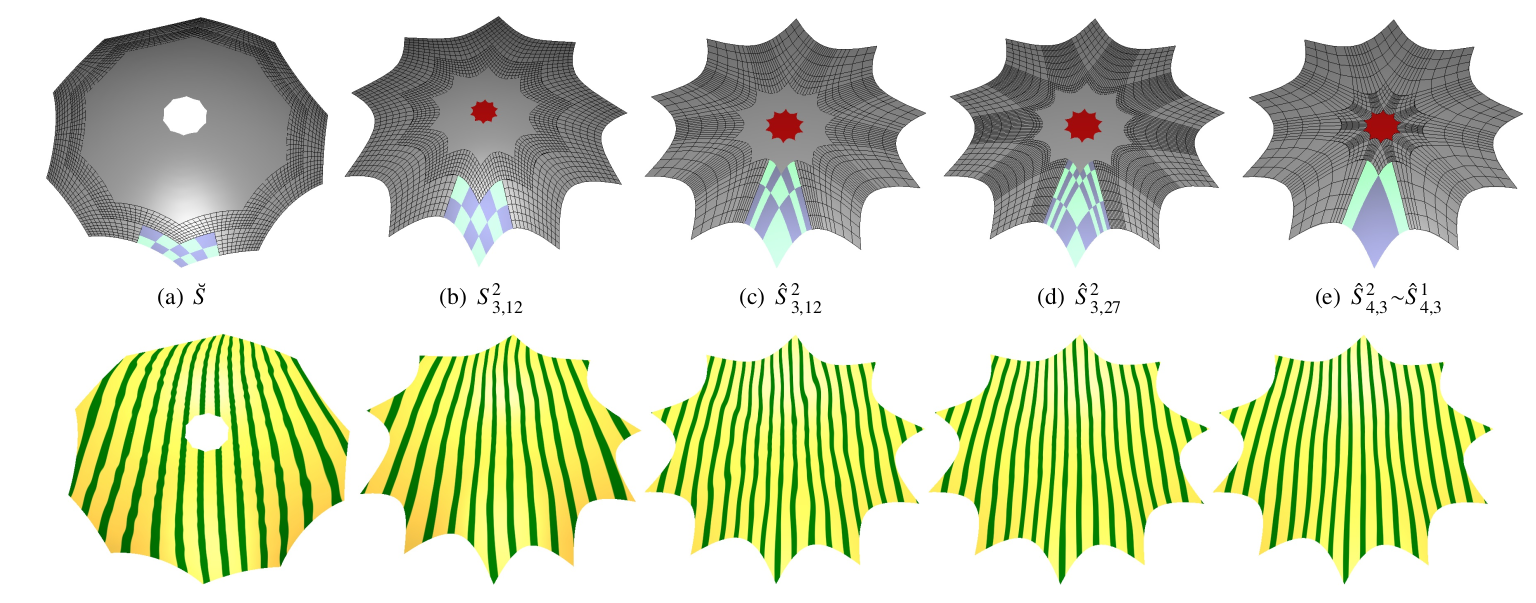
Merging parallel quad strips facilitates narrowing surface passages,
and allows a design to transition to simpler shape.
While a number of spline surface constructions exist for the isotropic case where n pieces
join, few existing spline constructions deliver good shape for control-nets that merge parameter
lines; and, until recently, none provided good shape for fast-contracting polyhedral control-nets.
This work improves the state-of-the-art of piecewise polynomial spline surfaces
accommodating fast-contracting control nets.
The new fast-contracting (FC) surface algorithm yields the industry-preferred uniform degree bi-3
(bi-cubic), the surfaces are by default differentiable, have improved shape,
measured empirically as highlight line distribution,
and require fewer pieces than the state-of-the-art.
abstract
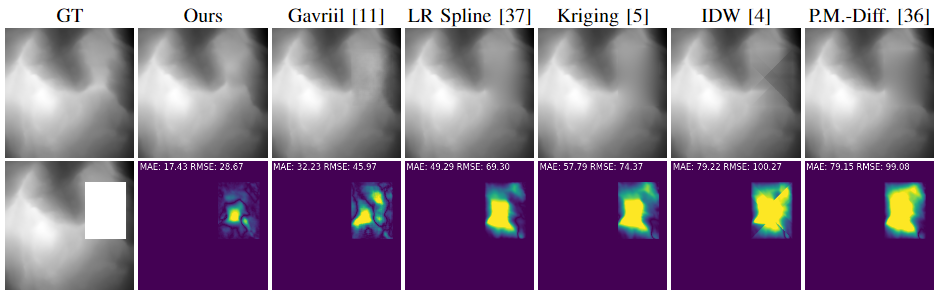
Digital Elevation Models (DEMs) are crucial for
modeling and analyzing terrestrial environments, but voids in
DEMs can compromise their downstream use. Diff-DEM is a
self-supervised method for filling DEM voids that leverages a
Denoising Diffusion Probabilistic Model (DDPM). Conditioned on
a void-containing DEM, the DDPM acts as a transition kernel
in the diffusion reversal, progressively reconstructing a sharp
and accurate DEM. Both qualitative and quantitative assessments
demonstrate Diff-DEM outperforms existing DEM inpainting, in-
cluding Generative Adversarial Network (GAN) methods, Inverse
Distance Weighting (IDW), Kriging, LR B-spline, and Perona-
Malik diffusion. The comparison is on Gavriilâs and on our
benchmark that expands Gavriilâs dataset from 63 to 217 full-
size (5051 Ã 5051) 10-meter GeoTIFF images sourced from
the Norwegian Mapping Authority; and from 50 DEMs to three
groups of 1k each of increasing void size.

abstract
Rapid reduction in the number of quad-strips, to accommodate narrower surface passages or reduced shape fluctuation, leads to
configurations that challenge existing spline surface constructions. A new spline surface construction for fast contracting polyhedral
control-nets delivers good shape. A nestedly refinable construction of piecewise degree (2,4) is compared with a uniform degree (3,3)
spline construction.
2023
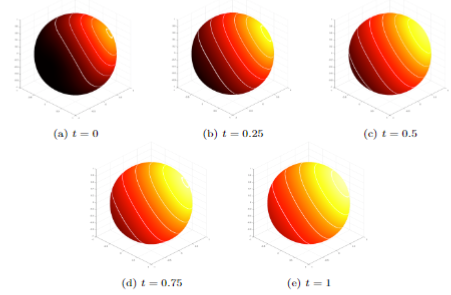
abstract
Generalizing tensor-product splines to smooth functions whose control nets can
outline more general topological polyhedra, bi-cubic polyhedral-net splines form
a first-order differentiable piecewise polynomial space. Each polyhedral con-
trol net node is associated with one bi-cubic function. A polyhedral control
net admits grid-, star-, n-gon-, polar- and three types of T-junction configu-
rations. Analogous to tensor-product splines, polyhedral-net splines can both
model curved geometry and represent higher-order functions on the geometry.
This paper explores the use of polyhedral-net splines for solving elliptic partial
differential equations on curved smooth free-form surfaces without additional
meshing.
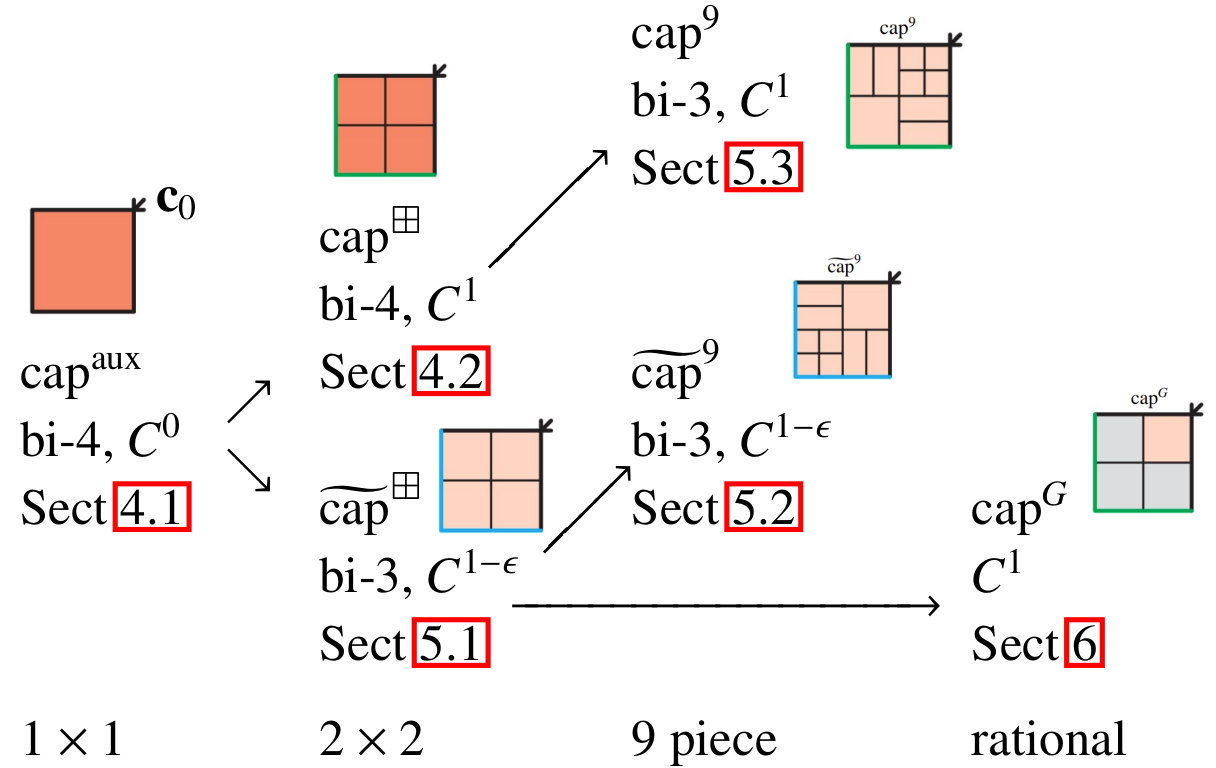
abstract
The quest for a finite number of bicubic (bi-3) polynomial pieces to smoothly fill multi-sided holes after a fixed number of surface
subdivision steps has motivated a number of constructions of finite surface caps. Recent bi-3 and bi-4 subdivision algorithms have
improved surface shape compared to classic Catmull-Clark and curvature-bounded âtunedâ subdivision. Since the older subdivision
algorithms exhibit artifacts that obscure the shortcomings of corresponding caps, it is worth re-visiting their multi-sided fill surfaces.
The improved caps address the challenge so that either bi-3 or bi-4 data can be accommodated, as needed. The derivation illustrates
the subtle fundamental trade off between formal algebraic mathematical smoothness constraints and good shape in the large.

abstract
The idea of improving multi-sided piecewise polynomial surfaces,
by explicitly prescribing their behavior at a central surface point,
allows for decoupling shape finding from enforcing local smoothness constraints.
Quadratic-Attraction Subdivision determines the completion of a quadratic expansion at the central point
to attract a differentiable subdivision surface towards bounded curvature, with good shape also in-the-large.
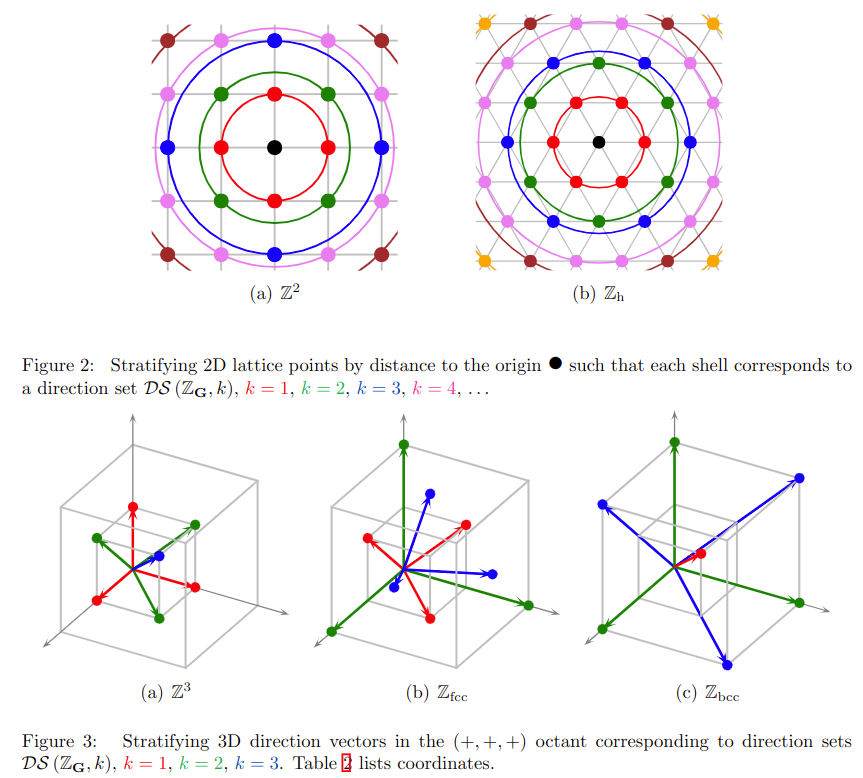
abstract
Box splines provide smooth spline spaces as shifts of a single generating function on
a lattice and so generalize tensor-product splines. Their elegant theory is laid out
in classical papers and a summarizing book. This compendium aims to succinctly but
exhaustively survey the specific important sub-space of symmetric low-degree box splines
on symmetric lattices with special focus on two and three variables. Tables contrast the
complexity in terms of support size and polynomial degree, analytic and reconstruction
properties, and list available implementations and code.

abstract
To overcome the well-known shape deficiencies of bi-cubic subdivision surfaces,
Evolving Guide subdivision (EG subdivision)
generalizes C
2 bi-quartic (bi-4) splines that approximate
a sequence of piecewise polynomial surface pieces near extraordinary
points. Unlike guided subdivision, which achieves good shape by following
a guide surface in a two-stage, geometry-dependent
process, EG subdivision is defined by five new explicit subdivision rules.
While formally only C
1 at extraordinary points, EG
subdivision applied to an obstacle course of inputs generates surfaces
without the oscillations and pinched highlight lines
typical for Catmull-Clark subdivision. EG subdivision surfaces join
C
2 with bi-3 surface pieces obtained by interpreting regular
sub-nets as bi-cubic tensor-product splines and
C
2
with adjacent EG surfaces. The EG subdivision control net surrounding
an extraordinary node can have the same structure as Catmull-Clark subdivision:
two rings of 4-sided facets around each
extraordinary nodes so that extraordinary nodes are separated by at least
one regular node.
2022
abstract
For control nets outlining a large class of topological polyhedra, not just tensor-product grids, bi-cubic
polyhedral splines form a piecewise polynomial, first-order differentiable space that associates one function
with each vertex. Akin to tensor-product splines, the resulting smooth surface approximates the polyhedron.
Admissible polyhedral control nets consist of quadrilateral faces in a grid-like layout, star-configuration
where n â 4 quadrilateral faces join around an interior vertex, n-gon configurations, where 2n quadrilaterals
surround an n-gon, polar configurations where a cone of n triangles meeting at a vertex is surrounded by a
ribbon of n quadrilaterals, and three types of T-junctions where two quad-strips merge into one.
The bi-cubic pieces of a polyhedral spline have matching derivatives along their break lines, possibly after
a known change of variables. The pieces are represented in Bernstein-Bézier form with coefficients depending
linearly on the polyhedral control net, so that evaluation, differentiation, integration, moments, etc. are no
more costly than for standard tensor-product splines. Bi-cubic polyhedral splines can be used both to model
geometry and for computing functions on the geometry. Although polyhedral splines do not offer nested
refinement by refinement of the control net, polyhedral splines support engineering analysis of curved smooth
objects. Coarse nets typically suffice since the splines efficiently model curved features. The code is a C++
library with input-output example pairs and an iges output choice.

abstract
Soft-tissue manipulations, such as collecting, stretching or
tearing tissue, are a common component of surgery. When too much
force is applied, these manipulations result in a residual plastic defor-
mation that surgeons should be aware of and that should be modeled
by surgical simulation.
abstract
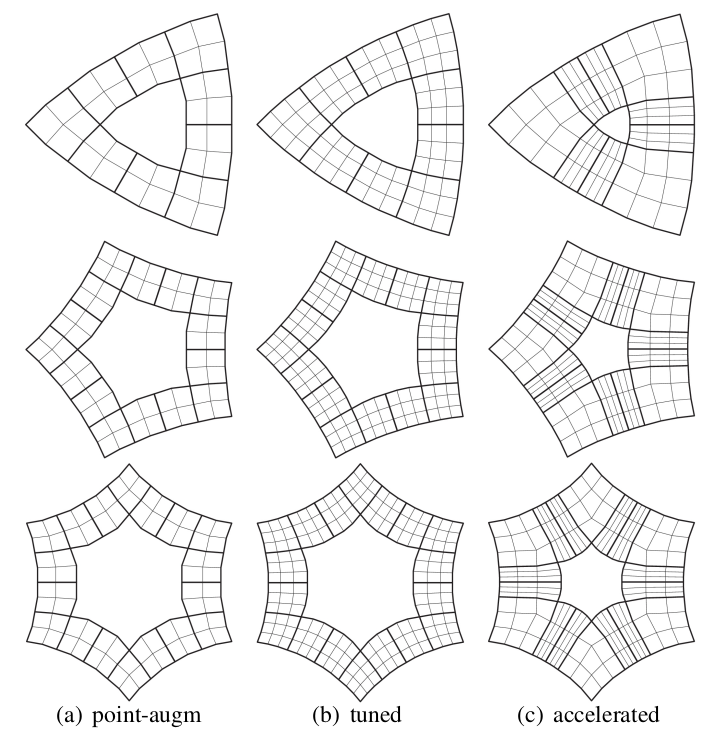
Point-Augmented Subdivision (PAS) replaces complex geometry-dependent guided subdivision,
known to yield high-quality surfaces, by explicit subdivision formulas that yield similarly-good limit surfaces
and are easy to implement using any subdivision infrastructure: map the control net
d
augmented by a fixed central limit point
C, to a finer net
(dË,C) = M(d,C), where the
subdivision matrix
M is assembled from the provided stencil Tables.
Point-augmented bi-cubic subdivision improves the state of the art so that bi-cubic subdivision surfaces
can be used in high-end geometric design: the highlight line distribution for
challenging configurations lacks the shape artifacts usually associated with explicit iterative
generalized subdivision operators near extraordinary points. Five explicit formulas define
Point-augmented bi-cubic subdivision in addition to uniform B-spline knot insertion.
Point-augmented bi-cubic subdivision comes in two flavors, either generating a sequence of C
2-joined surface
rings (PAS2) or C
1-joined rings (PAS1) that have fewer pieces.
abstract
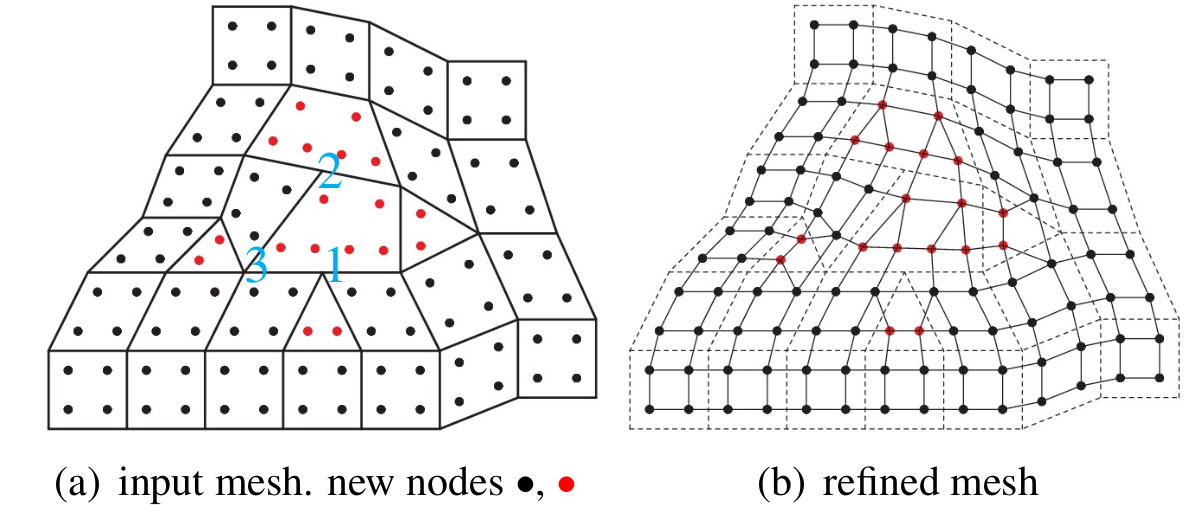
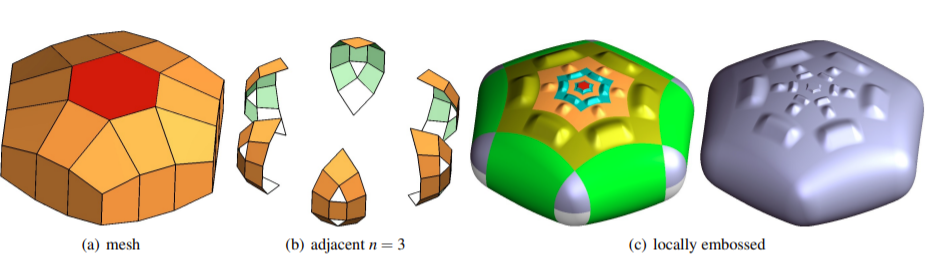
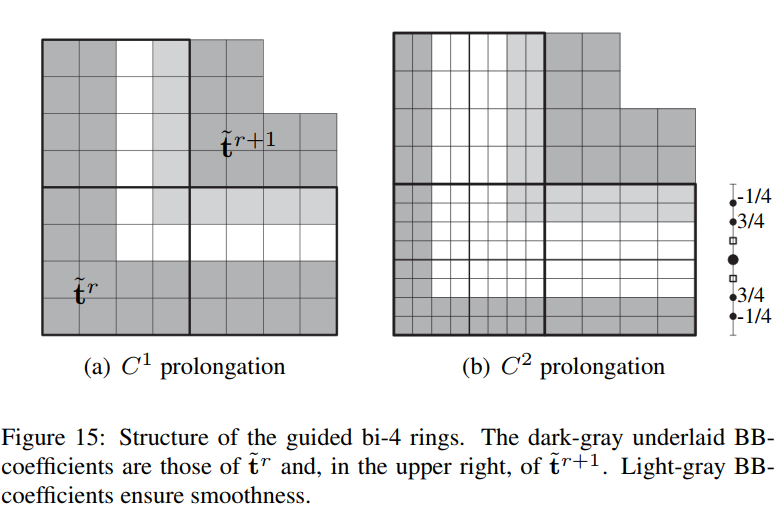
Smooth spline surfaces can now be built with polyhedral control nets rather than just grid-like tensor-product controlnets. However, irregularities such as T-junctions, multi-sided facets, andn-valent vertices need to be sufficiently sepa-rated. Automatically generated quad-dominant meshes, and meshes created by designers unaware of the requirementsfor spline surfaces often pack irregularities too tightly.Global refinement, e.g. via two steps of subdivision, can sufficiently separate irregularities. However, each refine-ment quadruples the number of polynomial pieces. Moreover, first-step artifacts can lead to oscillating and pinchedhighlight line distributions. We therefore investigate minimal, single edge insertion, re-connection and localized re-finement of quad-dominant meshes to make them suitable for polyhedral splines.
abstract
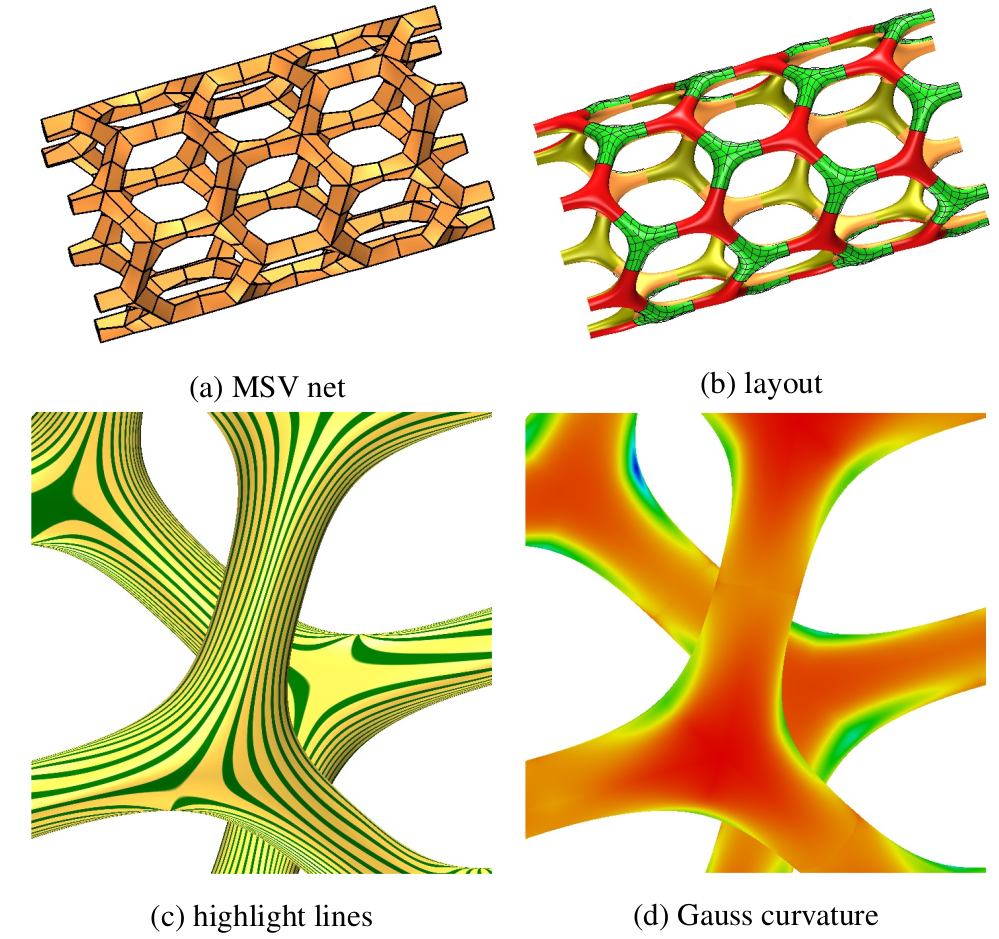
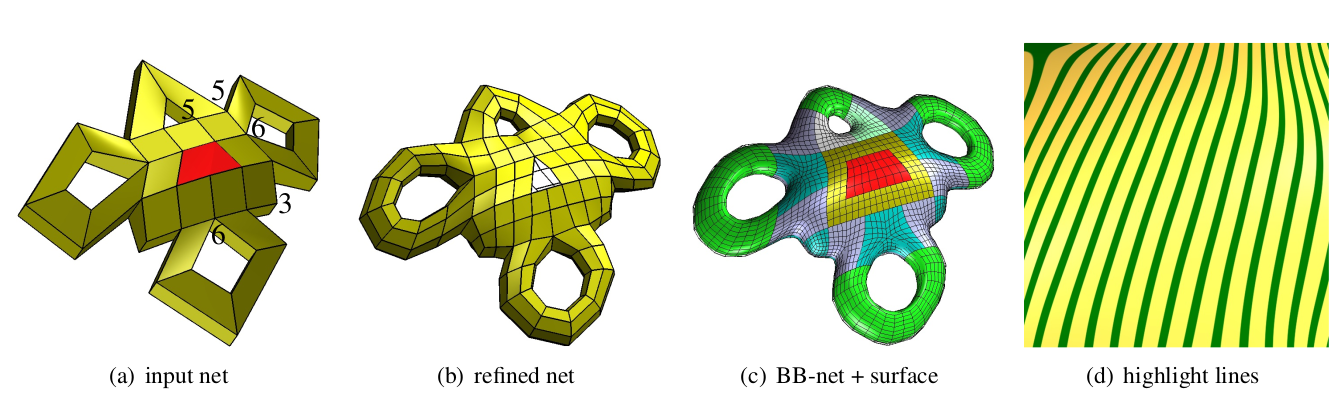
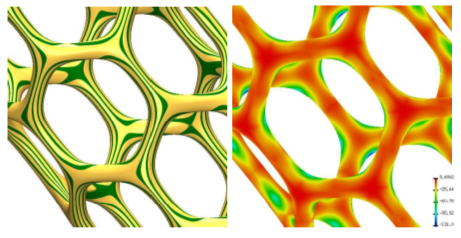
Scaffold-like surfaces, ranging from large-scale trusses to engineered micro-structures, are often sketched via repeating patterns ofnodes and edges. Offsetting these graphs turns them into meshes for which a smoothly-rounded scaffold surface âskinâ needs to belocally generated on the fly for production or analysis. We focus on minimal single-valence (MSV) quad meshes whose irregularvertices all have the same valencenand closest pairs are separated by exactly one regular, 4-valent vertex. Though at a first glancerather special, MSV meshes can model various micro-structures or trusses that occur in CAD or biology. Remarkably, bi-cubic patchesprovide a smooth skin of high quality, in many practical configurations with just one patch per quad.

abstract
The Toolkit for Illustration of Procedures in Surgery (TIPS) is an open source virtual reality (VR)
laparoscopic simulation-based training environment with force feedback. TIPS-author, is a content creation
interface that allows a surgeon-educator (SE) to assemble new laparoscopic training modules.
New technology enables safety rules to be specified by the SE, automatically tracks specified safety errors,
and summarizes and communicates achievements and errors to the surgical trainee.

abstract
Unstructured hex meshes are partitions of three spaces into boxes that can include irregular
edges, where n ̸≠: 4 boxes meet along an edge, and irregular points, where the box arrangement is
not consistent with a tensor-product grid. A new class of tri-cubic C
1 splines is evaluated as a tool for
solving elliptic higher-order partial differential equations over unstructured hex meshes.
Convergence rates for four levels of refinement are computed for an implementation of the isogeometric
Galerkin approach applied to Poissonâs equation and the biharmonic equation. The ratios of error
are contrasted and superior to an implementation of Catmull-Clark solids. For the trivariate Poisson
problem on irregularly partitioned domains, the reduction by 2
4 in the L
2 norm is consistent with
the optimal convergence on a regular grid, whereas the convergence rate for Catmull-Clark solids is
measured as O(h
3). The tri-cubic splines in the isogeometric framework correctly solve the trivariate
biharmonic equation, but the convergence rate in the irregular case is lower than O(h
4). An optimal
reduction of 2
4 is observed when the functions on the C
1 geometry are relaxed to be
C
0.
2021
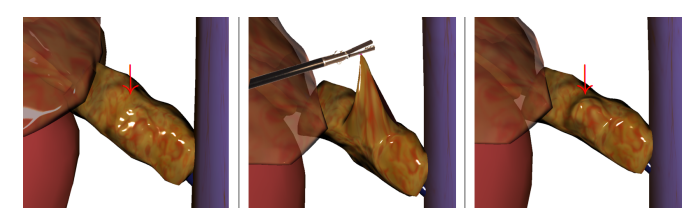
abstract
Collecting, stretching and tearing soft tissue is common in surgery.
These repeated deformations have a plastic component that surgeons take into consideration
and that surgical simulation should model.
Organs and tissues can often be modeled as curved cylinders or planes,
offset orthogonally to form thick shells. A pair of primary directions, e.g.,
axial and radial for cylinders, then provides a quadrilateral mesh whose
offset naturally yields a hexahedral mesh.
To better capture tissue plasticity for such hexahedral meshes, this work
compares to and extends existing volumetric finite element models of
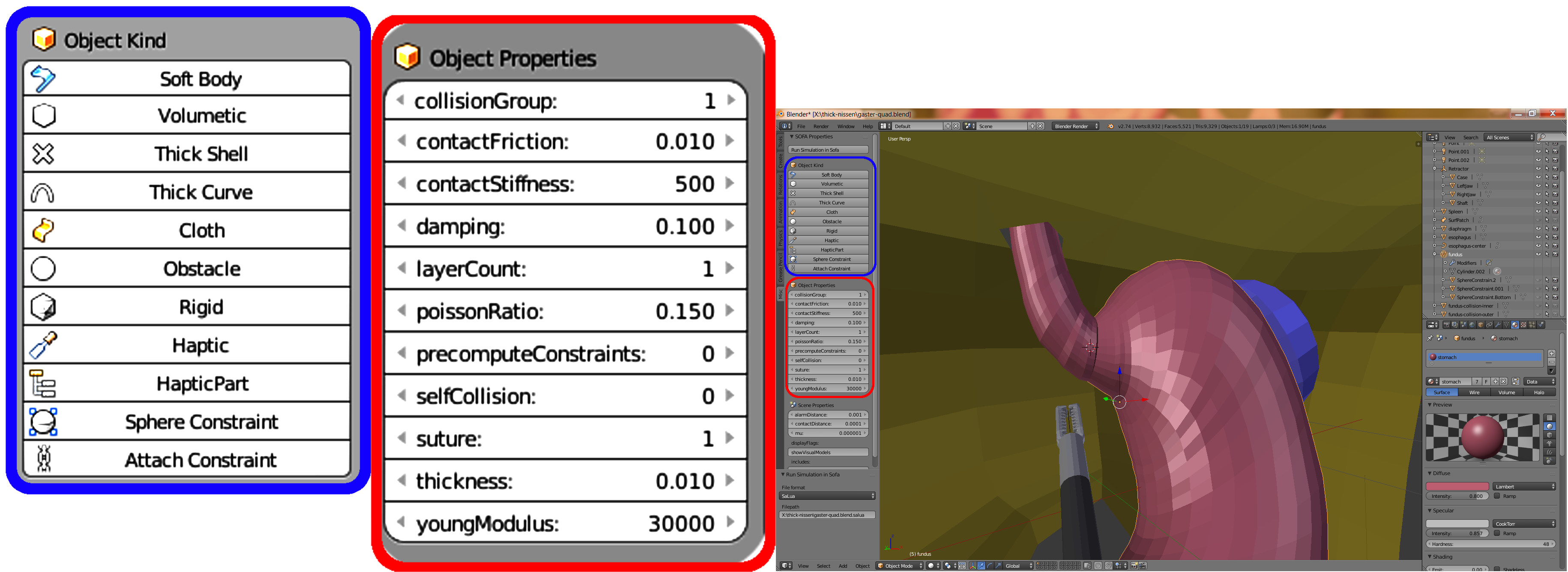
plasticity. Specifically, we extend the open source simulation framework
SOFA in the context of surgical simulation.
Based on factored deformation gradients, the extension focuses on the challenge of separating
symmetric and asymmetric, elastic and plastic deformation components
â while preserving volume and avoiding re-meshing.
abstract
When the full-scale storing and retrieving of volumetric models is cost prohibitive, intersection queries require intelligent access
to pieces generated on demand. To conform to a given curved outer shape without clipping, such models are often the result of a
non-linear free-form deformation applied to a geometrically simpler, canonical model. The additional challenge is then to relate the
intersection query back to the pieces of the pre-image of the conforming curved model.
Motivated by 3D print slice generation of massive mapped material micro-structure, this paper presents an algorithm to traverse a
planar slice of a volumetric mapped model that is too large to be treated as an explicit model. The algorithm safely reduces the largescale slicing problem to many small-scale problems that can be solved by existing slicing techniques. With the pre-image partitioned
into boxes, the algorithm activates boxes to generate micro-structure only where the non-linear image of the box can intersect the
given plane. Active boxes are intelligently traversed to guarantee both full coverage and minimize a front of active boxes.
abstract
Multi-sided faces arise in polyhedral modeling
through introduction of features not aligned with the
regular grid structure, e.g. when trimming off corners or
merging primary shapes.
A standard first step is to split the $n$-gon into
$n$ quadrilaterals that join at the $n$-gon's centroid.
A canonical example is the `face point rule' of Catmull-Clark subdivision.
We show that centroid-split rules negatively impact
shape -- already in the single, first refinement step.
A new alternative face (and edge) rule
improves the shape of surfaces controlled by the refined
mesh noticeably.
The improved face rule has a moderately increased footprint
compared to the Catmull-Clark rule
but remains simple in that it is characterized by just one
scalar weight for each $n$.
abstract
Subdivision surfaces based on bi-quadratic splines have a control net, the DS-net,
whose irregularities are $n$-sided facets.
To date their limit shape is poor due to a small footprint
of the refinement rules and the difficulty of
controlling shape at the center irregularity.
By contrast, a control net where vertices are surrounded by $n$ quadrilateral faces,
a CC-net,
admits higher-quality subdivision and finite polynomial constructions.
It would therefore be convenient to leverage these constructions
to fill holes in a $C^1$ bi-quadratic spline complex.
In principle the switch in layout from a control net with
central $n$-sided facet to one with a central irregular point is easy:
just apply one step of Catmull-Clark refinement.
The challenge, however, is to
define the transition between the bi-quadratic bulk
and the $n$-sided cap construction to be of sufficiently good shape
to not destroy the advantage of higher-quality algorithms.
This challenge is addressed here by explicit formulas for
conversion from a DS-net to a CC-net.
abstract
Traditionally the approach to filling $n$-sided
holes differs substantially for
bicubic $C^2$-splines vs
biquadratic $C^1$-splines due to
the \primal\ vs `dual' interpretation of the control net
that emphasises either $n$-valent vertices or $n$-sided facets.
Here we propose a construction that unites the treatment of both types
of spline surfaces, {notably} for {non-4-valent vertices in a quad-layout}.
The primal-dual-agnostic multi-sided surfaces are of degree bi-4.
Their main body can be chosen to be $C^1$
or $C^2$ and the remaining gap is filled by a tiny central $G^1$ cap.
2020
abstract
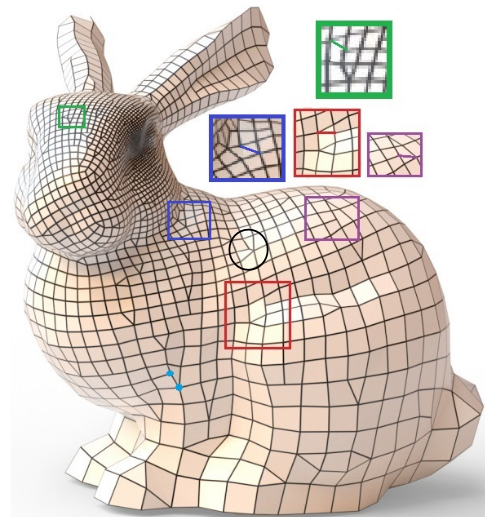
A mesh is locally quad-dominant (lqd) if all non-4-sided facets are surrounded
by quadrilaterals. Lqd meshes allow for irregular nodes where
more or fewer than four quads meet and for multi-sided facets, called T-gons,
that end quad-strips and so adjust mesh density.
This paper introduces a new class of bi-cubic (bi-3) Geometric T-joint (GT)
splines whose control nets are tau-nets, i.e. T-gons surrounded by quads.
These GT-splines join smoothly with each other, bi-3 G-splines and
regular C
1 bi-quadratic splines to form smooth surfaces
of degree at most bi-3.
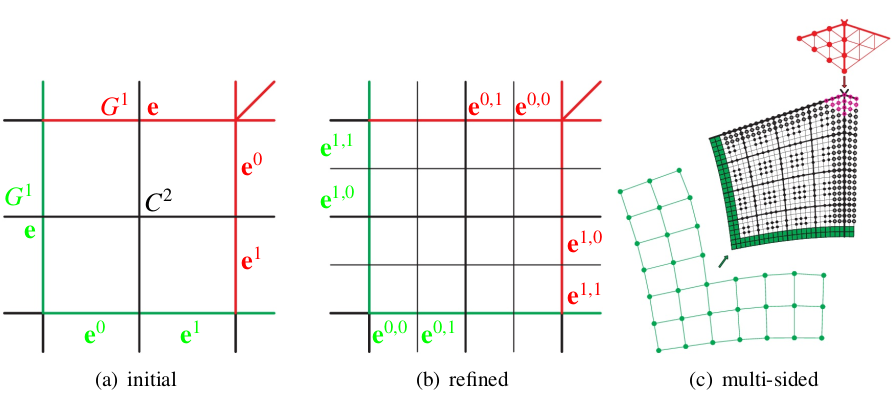
abstract
Refinement of a space of splines should yield
additional degrees of freedom for modeling and engineering analysis,
both along boundaries and in the interior.
Yet such additional flexibility fails to materialize
for multi-sided G
2 surface constructions
when the polynomial degree is too low.
This paper establishes a tight lower bound on the polynomial degree of
flexibility-increasing refinable multi-sided G
2
surface constructions within a C
2 spline complex --
by ruling out bi-5 constructions and by exhibiting a multi-sided
bi-6 construction
that yields good highlight line and curvature distributions.
The bi-6 construction consists of one 2 x 2 macro-patch for
each of the n sectors that join to form the multi-sided surface
Formulas (14), (19), (23) improve on the CAD paper
abstract
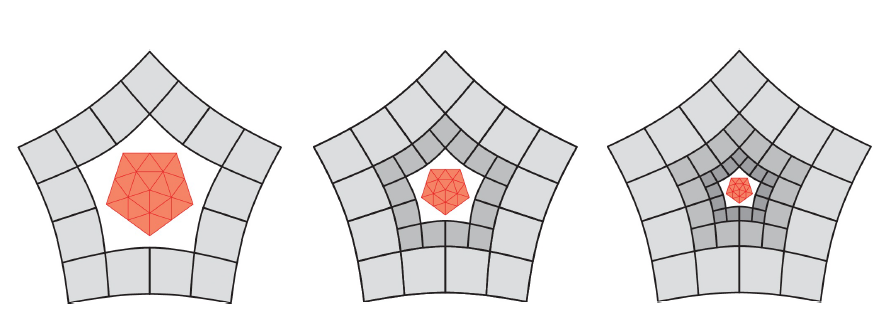
A polar configuration is a node surrounded by
m triangles.
Polar configurations are common to cap off cylinders and spheres.
When the triangles, interpreted as quadrilaterals
with one edge collapsed, are surrounded by a quad-strip then the extended polar
configuration qualifies as part of a locally quad-dominant (lqd) mesh.
Recent constructions, referred to as semi-structured splines,
can use lqd meshes as control nets: multi-sided configurations
that merge parameter directions are covered by G-spline; and T-junctions
that transition from coarse and fine are covered by GT-splines.
This paper complements existing semi-structured splines by providing
the missing component for polar configurations.
A spectrum of constructions of differing degree are
introduced, tested and compared.
Bi-2
C
1 splines are extended to polar configurations
covered by
C
1 surfaces consisting of (macro-)patches of degree as low as bi-2.
Bi-3
C
2
splines are extended to polar configurations covered by surfaces that are
C
2
except for a
C
1
pole and consist of (macro-)patches of degree as low as bi-3.
Geometrically smooth spline surfaces,
generalized to include
n-sided facets or configurations of
n <> 4
quads, can exhibit a curious lack of additional degrees of freedom
for modelling or engineering analysis when refined.
This paper establishes a minimal polynomial degree for smooth
constructions of multi-sided surfaces
that guarantees more flexibility in all directions under refinement.
Degree bi-4 is both necessary and sufficient for flexible
G
1-refinability within a bi-quadratic
C
1 spline complex.
Sufficiency is proven by two alternative
flexibly G
1-refinable constructions
exhibiting good highlight line distributions.
p6 correct a(u) BB-coefficients: 1,1, 2/(2-c)
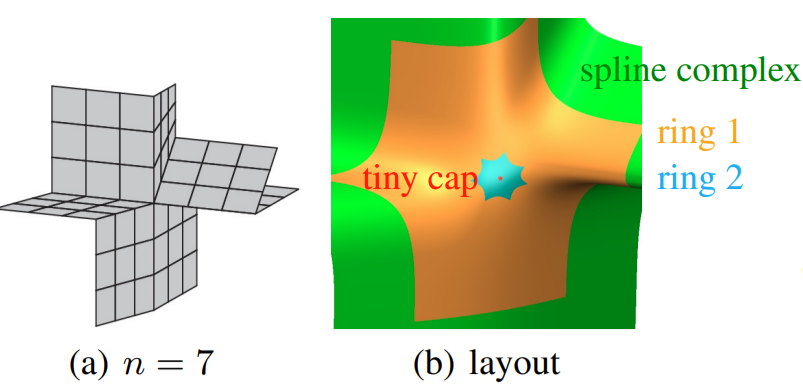
This survey of piecewise polynomial surface constructions for filling
multi-sided holes in a smooth spline complex
focusses on a class of hybrid constructions that, while heterogeneous,
combines all the practical advantages of state-of-the-art for
modelling and analysis:
good shape, easy implementation and
simple refinability up a pre-defined level.
After reviewing the three ingredients -- subdivision, G-spline and guided
surfaces -- the hybrid is defined to consist essentially of one
macro-patch for each of $n$ sectors, leaving just a tiny $n$-sided central
hole to be filled by a G-spline construction.
Here tiny means both geometrically small, e.g.
two orders of magnitude smaller than pieces of the spline complex,
and small in its contribution to engineering analysis,
i.e. it is unlikely to require further refinement
to express additional geometric detail or resolve a function on
the surface, such as the solution of a partial differential equation.
Each macro-patch has the local structure of a subdivision
surface near, but excluding the central, extraordinary point:
all internal transitions are the identity or scale according to
contraction speed toward the extraordinary point.
Both the number of pieces of the macro-patches and the speed
can be chosen application-dependent and adaptively.
2019
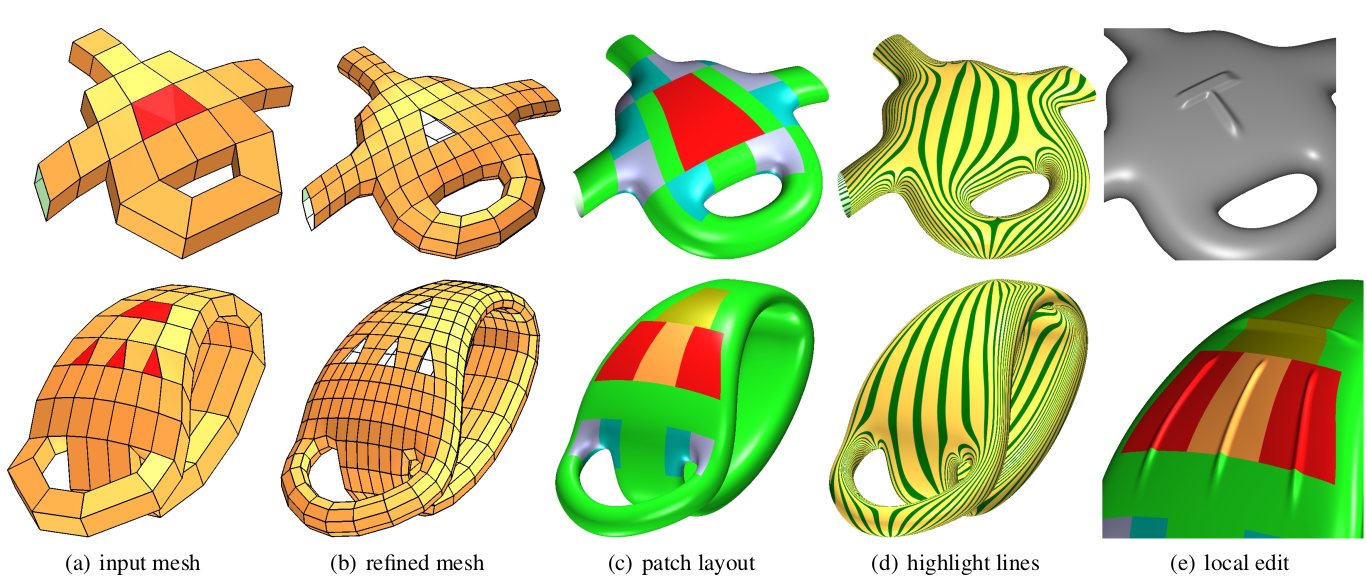
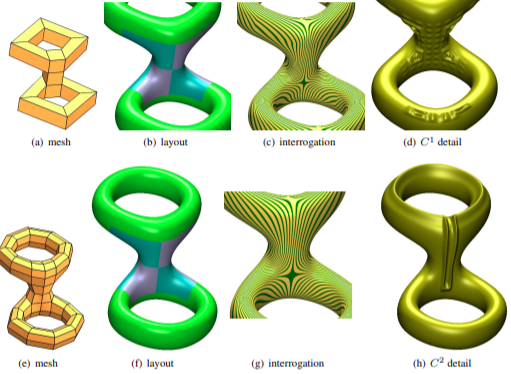
abstract
Polyhedral modeling and re-meshing algorithms use T-junctions
to add or remove feature lines in a quadrilateral mesh.
In many ways this is akin to adaptive knot insertion in
a tensor-product spline, but differs in that the designer or
meshing algorithm does not necessarily protect the consistent
combinatorial structure that is required to interpret
the resulting quad-dominant mesh as the control net of a hierarchical
spline -- and so associate a smooth surface with the mesh
as in the popular tensor-product spline paradigm.
While G-splines for multi-sided holes or generalized subdivision
can, in principle, convert quad-dominant meshes with T-junctions into
smooth surfaces, they do not preserve the two preferred directions
and so cause visible shape artifacts.
Only recently have n-gons with T-junctions (T-gons) in unstructured
quad-dominant meshes been recognized as a distinct challenge
for generalized splines.
This paper makes precise the notion of
locally quad-dominant mesh
as quad-meshes including τ-nets, i.e. T-gons surrounded by quads;
and presents the first high-quality G-spline construction
that can use τ-nets as control nets for spline surfaces
suitable, e.g., for automobile outer surfaces.
Remarkably, T-gons can be neighbors, separated by only one quad,
both of T-gons and of points where many quads meet.
A τ-net surface cap consists of 16 polynomial pieces
of degree (3,5) and is refinable in a way that is
consistent with the surrounding surface.
An alternative, everywhere bi-3 cap is not formally smooth,
but achieves the same high-quality highlight line distribution.
abstract
Splines form an elegant bridge between
the continuous real world and the discrete computational world.
Their tensor-product form lifts many univariate properties
effortlessly to the surfaces, volumes and beyond.
Irregularities, where the tensor-structure breaks down,
therefore deserve attention -- and provide a rich
source of mathematical challenges and insights.
This paper reviews and categorizes techniques for
splines on meshes with irregularities. Of particular interest
are quad-dominant meshes that can have
n≠ 4-valent
interior points and T-junctions where
quad-strips end. 'Generalized' splines can use quad-dominant
meshes as control nets both for modeling geometry and
to support engineering analysis without additional meshing.
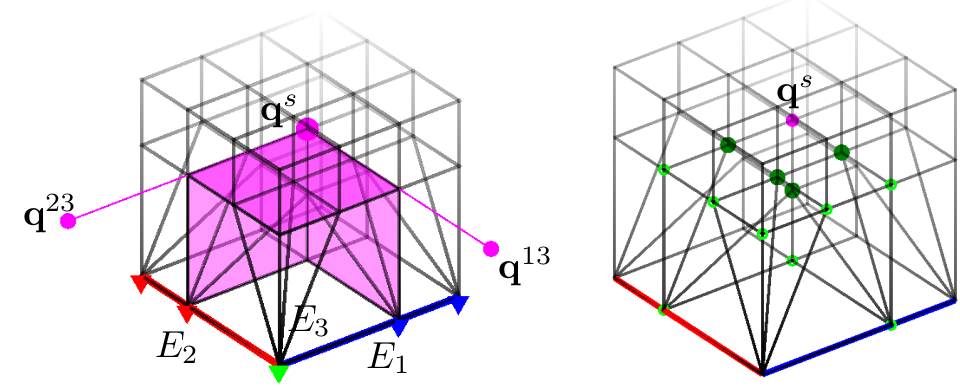
abstract
C
1 splines over box-complexes generalize
C
1 degree 3 (cubic) tensor-product splines.
A box-complex is a collection of 3-dimensional boxes forming an
unstructured hexahedral mesh that can include irregular points and
irregular edges where the layout deviates from the tensor-product grid layout.
For example, an edge shared and enclosed by five boxes is irregular.
Where the mesh is locally regular, the restriction of the space to each box
is a polynomial piece of the
C
1 tri-cubic tensor-product spline, by default initialized as a
C
2 tri-cubic. Boxes containing irregularities have their
polynomials binarily split into
2
3 pieces to isolate the irregularity.
The pieces join with matching derivatives.
The derivatives are zero at irregularities, but these singularities
are removable by a local change of variables. The space
consists of
2
3 linearly independent functions per box and is refinable.
abstract
A sequence of C
2-connected nested subdivision rings of
polynomial degree bi-4 can be made to follow a guide surface
and completed by a tiny finite cap to serve as a refinable surface
representation for design and analysis [RBDA =
Refinable bi-quartics for design and analysis, Computer-Aided Design (2018)].
This raises the question, both of academic and practical interest, how much
and at what cost to surface quality can the efficiency be improved
by lowering the number of rings and/or the polynomial degree.
In a systematic exploration, a new bi-4 construction is discovered
that requires half the number of surface rings
but matches the quality of [RBDA].
For this surface quality, numerous trials indicate that
this number of surface rings is minimal and that
the degree can not be reduced. Bi-3 constructions with a similar layout have
inferior highlight line distributions -- although
the best of the new bi-3 constructions visibly improve on Catmull-Clark
subdivision and its curvature-bounded variants.
abstract
Multi-sided facets in polyhedral models and meshes serve to connect regular sub-
meshes (star-configurations) and to start or end quad-strips (T-configurations). Using
the polyhedral mesh as control net, recursive subdivision algorithms often yield poor
shape for these non-quad configurations. Polynomial surface constructions such as ge-
ometrically smooth splines (G-splines) do better, but lack subdivision-like refinability.
Such refinability is useful for hierarchical modeling and engineering analysis.
This paper introduces a new class of G-splines that generalizes bi-quadratic C
1
splines to polyhedral control nets with star- and T-configurations and that is refinable.
abstract
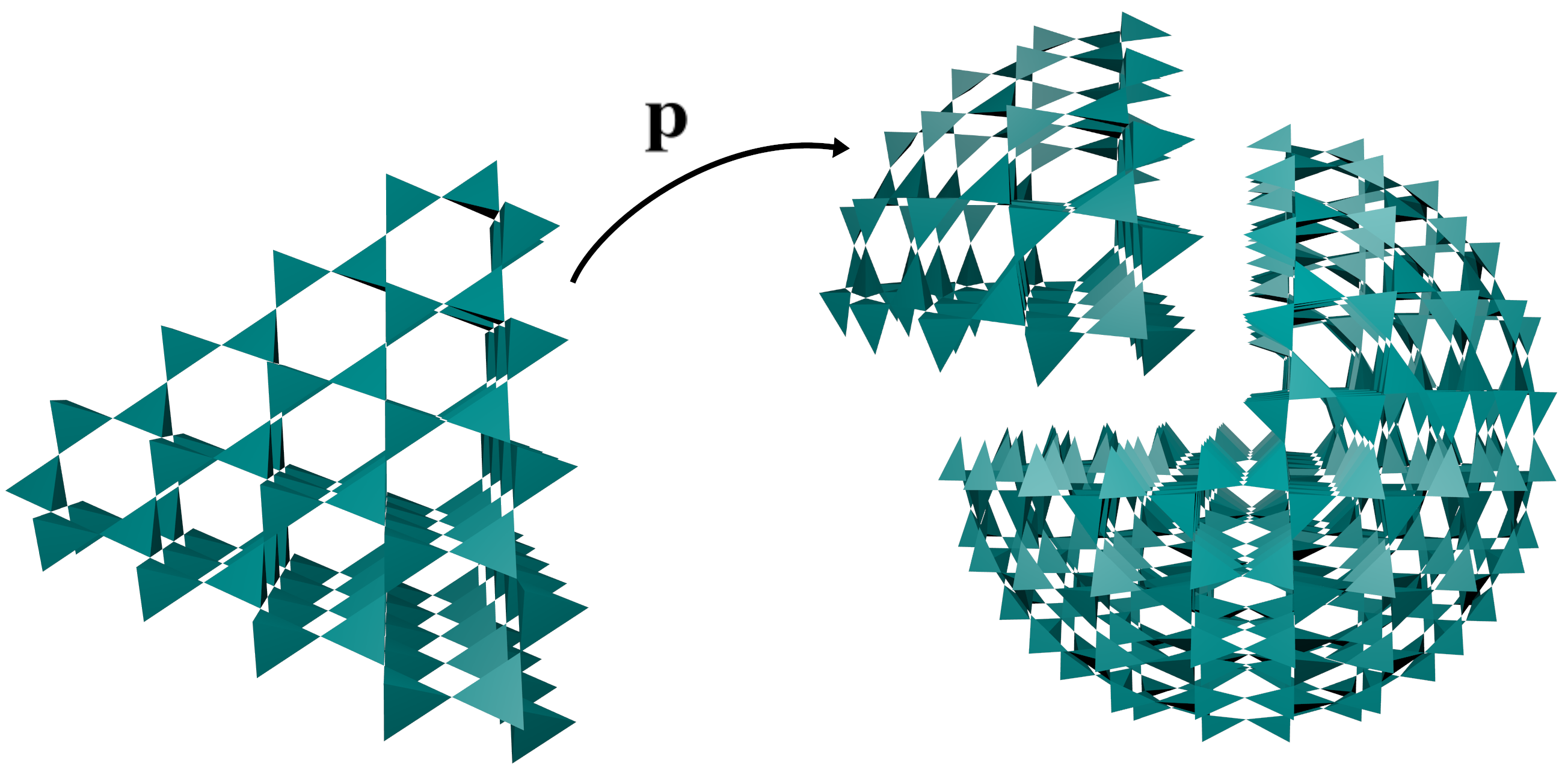
This paper introduces Corner-Sharing Tetrahedra (CoSTs), a minimalist, constraint-graph representation of micro-structure. CoSTs
have built-in structural guarantees, such as connectivity and minimal rigidity. CoSTs form a space, fully accessible via local operations,
that is rich enough to design regular or irregular micro-structure at multiple scales within curved objects. All operations are based on
efficient local graph manipulation, which also enables efficient analysis and adjustment of static physical properties. Geometric and
material detail, parametric or solid splines, can be added locally, on-demand, for example, for printing.
Def 4 has corrected formula for Kagome points
abstract
Enriching tensor-product B-spline control nets by allowing T-gons
(where strips of quadrilaterals start or end) and
irregular nodes (where n != 4 quadrilaterals meet)
reduces the requirements on quad-meshing and increases the flexi bility
for polyhedral design with associated smooth surfaces.
This paper introduces a family of piecewise polynomial,
geometrically continuous surface constructions that yield good highlight line
distributions also in the presence of irregular nodes next to a T-gon.
Such tight juxtaposition can further reduce the quad-meshing requirements
and increase the space of polyhedral design control structures.
The surfaces can be chosen to cover T-gons with G
1
caps of degree bi-4 â or with caps of degree bi-3 that are
almost G
1 and preserve the good highlight line distribution
of the bi-4 G
1 surfaces.
2018
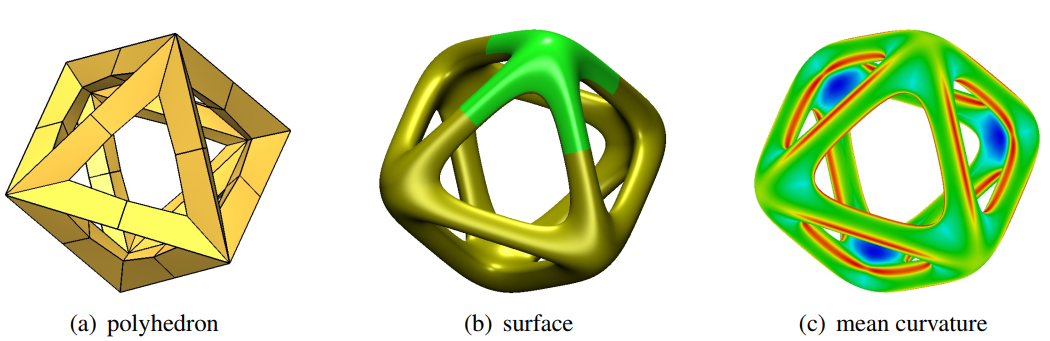
abstract
Compared to G
k continuity, C
k continuity simplifies the construction of functions on surfaces and their refinement,
e.g. to solve differential equations on the surface. The new class of almost everywhere parametrically C
2 free-form
surfaces provide such a parameterization. For example, a new bi-6 construction combines a fast-contracting C
2guided
subdivision surface with a tiny multi-sided G
1 cap. The cap is chosen to be smaller than any refinement anticipated for
geometric modeling or computing on surfaces. Fast contraction means that one subdivision step shrinks the remaining
hole more than three steps of Catmull-Clark subdivision. This yields smooth surfaces consisting of a finite number
of pieces that are suitable for engineering practice. Both the subdivision construction and the cap are guided by a
reference surface. This guide conveys the basic shape, but has a different structure and lower smoothness.
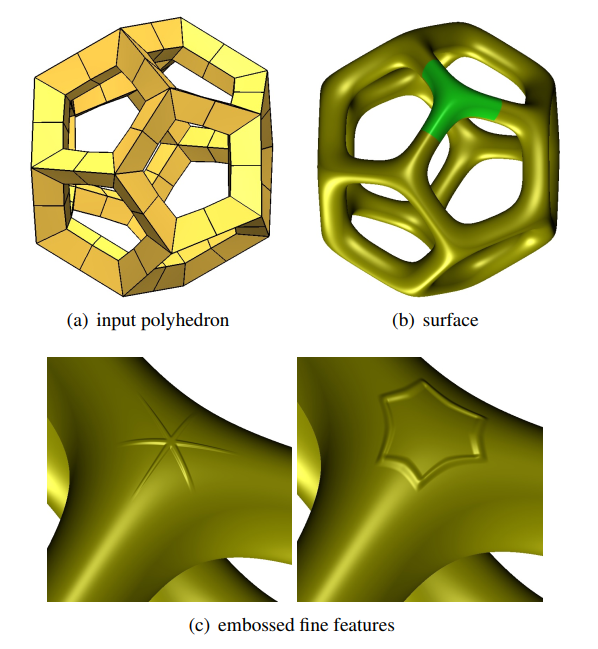
abstract
To be directly useful both for shape design and a thin shell analysis, a surface representation has to satisfy three properties: (1) be
compatible with CAD surface representations, (2) yield generically a good highlight distribution, and (3) offer a refinable space of
functions on the surface. Here we propose a new construction, based on a number of recently-developed techniques, that satisfies
all three criteria. The construction converts quad meshes with irregularities, where more or fewer than four quads meet, to C
1 (or,
at the cost of more pieces, C
2) bi-4 surface consisting of subdivision rings for the main body completed by a tiny G
1 cap.
abstract
Tools of subdivision theory allow constructing surfaces that are effectively C
2 and have
a good highlight line distribution also near irregularities where more or fewer than four
quadrilateral patches meet. Here, effectively C
2 means that transitions that are only
first-order smooth are confined to a tiny multi-sided cap. The cap can be chosen smaller
than any refinement required for geometric modeling or computing on surfaces. The
remainder of the surface parameterization is C
2. The resulting surface is of degree bi-5
and consists of three or fewer surface rings that are rapidly converging towards the tiny
central cap.
abstract
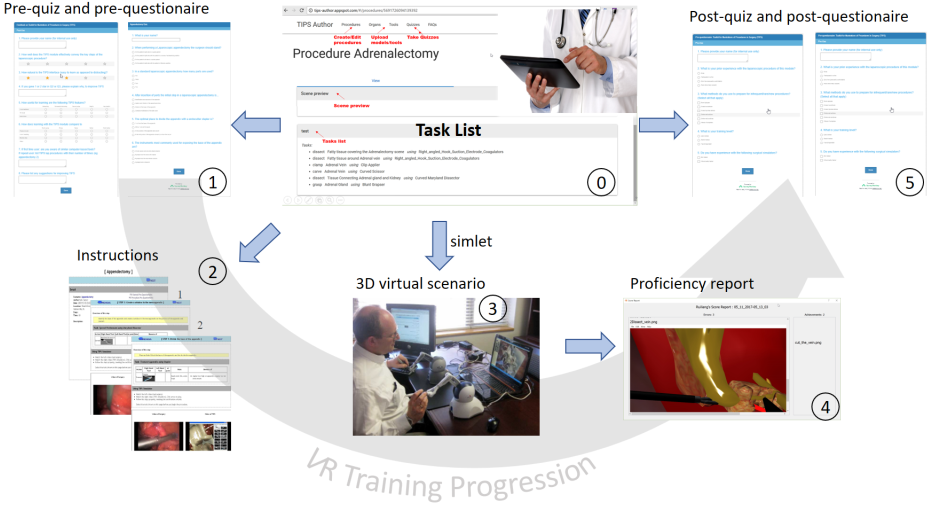
Enabling surgeon-educators to create VR-training units promises greater variety, specialization and relevance of the units. It allows implementing variation
in technique, an important component of traditional surgical education, and to
create uncommon and specialized scenarios.
We report on a web-based authoring interface that allows surgeon-educators
to assemble simulation-ready pieces of VR anatomy and tools to quickly specify
new surgical scenarios. This interface has successfully been used by surgeoneducators to create laparoscopic training units for appendectomy, cholecystectomy and adrenalectomy.
2017
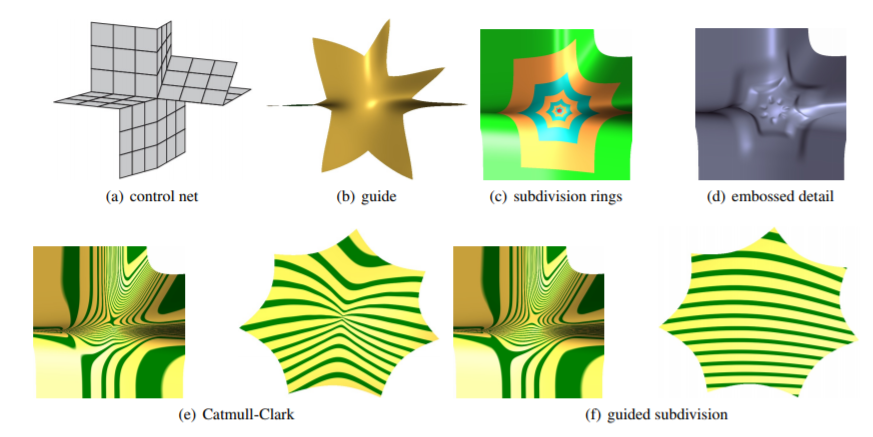
abstract
Converting quadrilateral meshes to smooth manifolds, guided subdivision offers a way to combine the good highlight line
distribution of recent G-spline constructions with the refinability of subdivision surfaces. This avoids the complex refinement of
G-spline constructions and the poor shape of standard subdivision. Guided subdivision can then be used both to generate the
surface and hierarchically compute functions on the surface.
Specifically, we present a C
2 subdivision algorithm of polynomial degree bi-6 and a curvature bounded algorithm of degree bi-5.
We prove that the common eigen-structure of this class of subdivision algorithms is determined by their guide and demonstrate
that their eigenspectrum (speed of contraction) can be adjusted without harming the shape.
For practical implementation, a finite number of subdivision steps can be completed by a high-quality cap. Near irregular points
this allows leveraging standard polynomial tools both for rendering of the surface and for approximately integrating functions
on the surface.
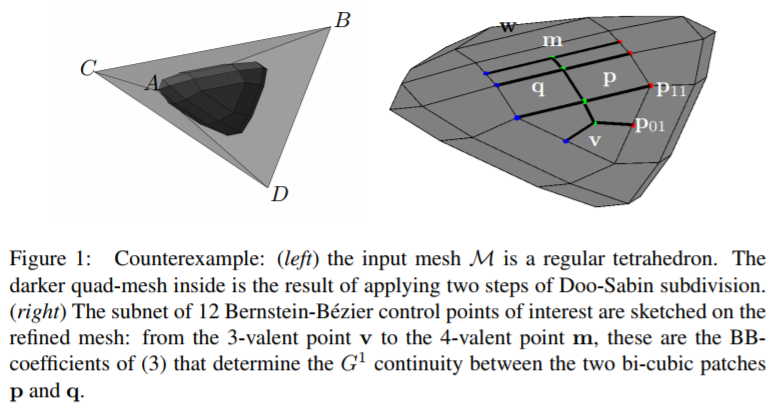
abstract
Lower bounds, mandating a minimal number and degree of polynomial pieces,
represent a major achievement in the theory of geometrically smooth (G
1) constructions. On one hand, they establish a floor when searching for optimal constructions, on the other they can be used to flag complex constructions for potential
flaws. In particular, quadrilateral meshes of arbitrary topology can not in general
be converted to G1-connected Bezier patches of bi-degree 3 with one piece per ´
quad or use just linear reparameterizations. This note illustrates how lower bounds
indicate otherwise difficult-to-find flaws in a complex new surface construction.
abstract
T-junctions occur where surface strips start or terminate. This paper de-
velops a new way to create smooth piecewise polynomial free-form spline
surfaces from quad-meshes that include T-junctions. All mesh nodes are
interpreted as control points of GT-splines, i.e. geometrically smoothly
joined piecewise polynomials. GT-splines are akin to and compatible with
B-splines and cover simple T-junctions by two polynomial pieces of degree
bi-4 and more complex ones by four such patches. They complement multi-
sided surface constructions in generating free-form surfaces with adaptive
layout.
Since GT-splines do not require a global coordination of knot intervals,
GT-constructions are easy to deploy and can provide smooth surfaces with
T-junctions where T-splines can not have a smooth parameterization. GT-
constructions display a uniform highlight line distribution on input meshes
where alternatives, such as Catmull-Clark subdivision, exhibit oscillations.

abstract
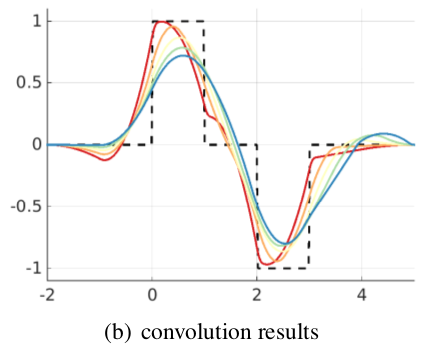
Convolving the output of Discontinuous Galerkin (DG) computations
using spline filters can improve both smoothness and accuracy
of the output. At domain boundaries, these filters have to be
one-sided for non-periodic boundary conditions. Recently,
position-dependent smoothness-increasing
accuracy-preserving (PSIAC) filters were shown to be
a superset of the well-known one-sided RLKV and SRV filters.
Since PSIAC filters can be formulated symbolically, PSIAC
filtering amounts to forming linear products with local DG output
and so offers a more stable and efficient implementation.
The paper introduces a new class of PSIAC filters NP
0
that have small support and are piecewise constant.
Extensive numerical experiments for the canonical hyperbolic test
equation show NP
0
filters outperform the more complex known boundary filters.
NP
0 filters typically reduce the L
â error
in the boundary region below that of the interior where
optimally superconvergent symmetric filters
of the same support are applied. NP
0
filtering can be implemented as forming linear combinations of
the data with short rational weights. Exact derivatives of the
convolved output are easy to compute.

abstract
To date, singularly-parameterized surface constructions suffer from
poor highlight line distributions, ruling them out as a surface
representation of choice for primary design surfaces.
This paper explores graded, many-piece, everywhere $C^1$
singularly-parameterized surface caps
that mimic the shape of a high-quality guide surface.
The approach illustrates the
trade-off between polynomial degree and surface quality.
For bi-degree 5, minor flaws in the highlight line distribution
are still visible when zooming in on the singularity,
but the distribution is good at the macroscopic level.
Constructions of degree bi-4 or bi-3 may require one or more steps
of guided subdivision to reach the same macroscopic quality.
Akin to subdivision surfaces, singularly-parameterized functions
on the surfaces are straightforward to refine.

abstract
For two high-quality piecewise polynomial geometrically smooth (G
1)
surface constructions, explicit G
1 functions are derived
that form the basis of a functions space on the G
1 surfaces.
The spaces are refinable and nested, i.e. the functions can be
re-represented at a finer level. By choosing all basis functions
to be first order smooth a maximal set of degrees of freedom is
obtained that have small support and near-uniform layout.

abstract
The study assesses user acceptance and effectiveness of a surgeon-authored virtual reality (VR) training
module authored by surgeons using the Toolkit for Illustration of Procedures in Surgery (TIPS). Laparoscopic
adrenalectomy was selected to test the TIPS framework on an unusual and complex procedure. No commercial
simulation module exists to teach this procedure. A specialist surgeon authored the module, including force-feedback
interactive simulation, and designed a quiz to test knowledge of the key procedural steps. Five practicing surgeons,
with 15 to 24 years of experience, peer reviewed and tested the module. In all, 14 residents and 9 fellows trained
with the module and answered the quiz, preuse and postuse. Participants received an overview during Surgical Grand
Rounds session and a 20-minute one-on-one tutorial followed by 30 minutes of instruction in addition to a forcefeedback interactive simulation session.
Additionally, in answering questionnaires, the trainees reflected on their
learning experience and their experience with the TIPS framework. Results. Correct quiz response rates on procedural
steps improved significantly postuse over preuse. In the questionnaire, 96% of the respondents stated that the TIPS
module prepares them well or very well for the adrenalectomy, and 87% indicated that the module successfully
teaches the steps of the procedure. All participants indicated that they preferred the module compared to training
using purely physical props, one-on-one teaching, medical atlases, and video recordings. Conclusions. Improved quiz
scores and endorsement by the participants of the TIPS adrenalectomy module establish the viability of surgeons
authoring VR training
2016

abstract
Polycube G-splines form a 2-manifold guided by a mesh of quadrilateral faces such that at most six quads meet at each vertex. In
particular, this replicates the layout of the quad faces of a polycube. Polycube G-splines are piecewise bicubic and polycube Gspline
surfaces are almost everywhere tangent-continuous (G
1) based on rational linear reparameterization. They can be constructed
in two different ways. One construction interprets the quad mesh vertices in the fashion of C
2 bicubic splines â this provides for
good shape; the other interprets the $2\times2$ inner B´ezier coefficients of each bicubic as C
1 bicubic B-spline coefficients â this offers
four degrees of freedom per patch and enables adaptive refinement so that the resulting G-spline spaces are nested, i.e. any G-spline
surface can be exactly re-represented at different levels of refinement.
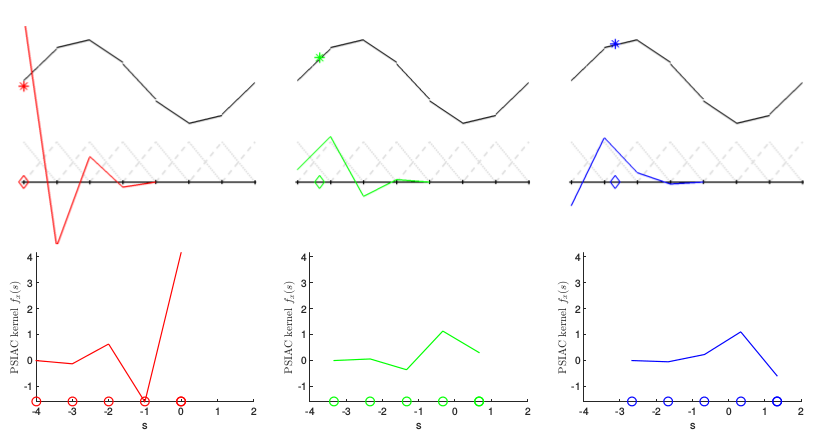
abstract
Convolving the output of Discontinuous Galerkin computations
with symmetric Smoothness-Increasing Accuracy-Conserving
(SIAC) filters can improve both smoothness and accuracy.
To extend convolution to the boundaries, several
one-sided spline
filters have recently been developed.
This paper interprets these filters as instances of a general class
of position-dependent (PSIAC) spline filters that
can have non-uniform knot sequences
and skip B-splines of the sequence.
PSIAC filters with rational knot sequences have rational coefficients.
For prototype knot sequences, such as integer sequences that may have
repeated entries, PSIAC filters can be expressed in symbolic form.
Based on the insight that filters for shifted or scaled knot sequences
are easily derived by non-uniform scaling of one prototype filter,
simplifies to forming a scalar product of a short vector
with the local output data. Restating one-sided filters in this form
improves both stability and efficiency
compared to their original formulation via numerical integration.
PSIAC filtering is demonstrated for several established
and one new boundary filter.
abstract
Building on a result of U. Reif on removable singularities, we construct
C
1 bi-3 splines that may include irregular
points where less or more than four tensor-product patches meet. The resulting space complements PHT splines,
is refinable and the refined spaces are nested, preserving for example surfaces constructed from the splines. As in
the regular case, each quadrilateral has four degrees of freedom, each associated with one spline and the splines are
linearly independent. Examples of use for surface construction and isogeometric analysis are provided.
typo p4, Average: (..)/2
Questions by (Zhihui Zou, Michael A. Scott)
USACM 2016 talk
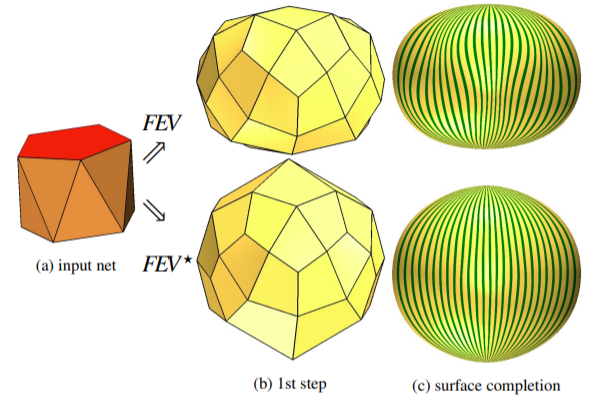
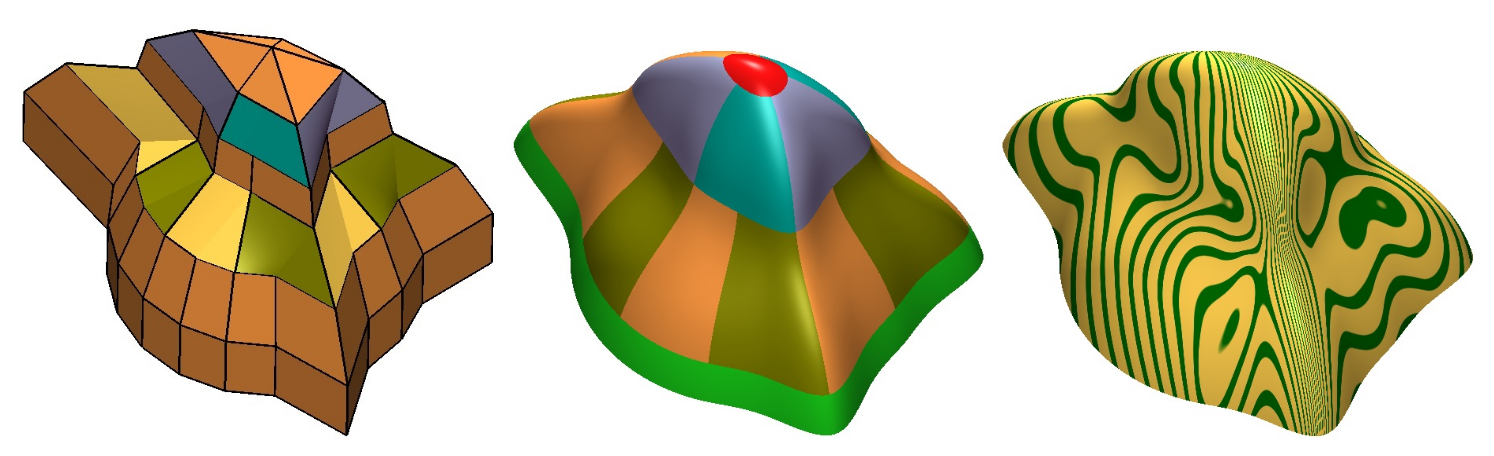
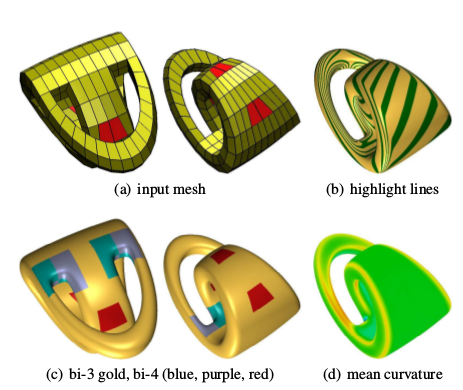
abstract
Scaffold surfaces bound geometric structures that have
a dual characterization as a curve network and a solid.
A subset of scaffold surfaces
can be modeled with minimal single-valence (MSV) meshes,
i.e.\ meshes consisting of vertices of a single irregular valence $n$
two of which are separated by exactly one regular, 4-valent vertex.
We present an algorithm for constructing piecewise bi-quartic surfaces that
join with curvature continuity to form scaffold surfaces for MSV meshes,
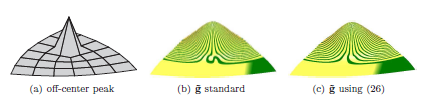
for $n=5,\ldots,10$.
Additionally, for sphere-like meshes,
we exhibit bi-quartic curvature continuous surfaces with
polar parameterization.
abstract
Enabling surgeon-educators to themselves create virtual reality (VR)
training units promises greater variety, specialization and relevance
of the units.
This paper describes a software bridge that semi-automates
the scene-generation cycle, a key bottleneck in authoring, modeling and
developing VR units.
Augmenting an open-source modeling environment with physical behavior
attachment and collision specifications yields single-click
testing of the full force-feedback enabled anatomical scene.
2015

abstract
This paper addresses a gap in the arsenal of
curvature continuous tensor-product spline constructions:
an algorithm is provided to fill $n$-sided holes in C
2 bi-3 spline
surfaces using $n$ patches of degree bi-6.
Numerous experiments illustrate good highlight line and
curvature distribution on the resulting surfaces.
The functional $\mathcal{F}_k$ in (14) should read
$(\partial^i_s\partial^j_tf)^2$ not $(\partial^i_s f\partial^j_tf)^2$;
and in (3) $\partial_u f \partial_v f$ should be $\partial_u\partial_v f$
abstract
Quad meshes can be interpreted as tensor-product spline control meshes
as long as they form a regular grid, locally.
We present a new option for complementing bi-3 splines by bi-4 splines
near irregularities in the mesh layout, where less or more than four
quadrilaterals join. These new generalized surface and IGA
(isogeometric analysis) elements have as their degrees of freedom the
vertices of the irregular quad mesh.
From a geometric design point of view, the new construction distinguishes
itself from earlier work by a notably better distribution of highlight lines.
From the IGA point of view, increased smoothness and reproduction at
the irregular point yield fast convergence.
The functional $\mathcal{F}_k$ in Sec 2.3 should read
$(\partial^i_s\partial^j_tf)^2$ not
$(\partial^i_s f\partial^j_tf)^2$
abstract
The discontinuous Galerkin (dG) method
outputs a sequence of polynomial pieces. Post-processing the sequence by
Smoothness-Increasing Accuracy-Conserving (SIAC) convolution
not only increases the smoothness of the sequence
but can also improve its accuracy and yield superconvergence.
SIAC convolution is considered optimal if the
SIAC kernels, in the form of a linear combination of B-splines
of degree $d$, reproduce polynomials of degree $2d$.
This paper derives simple formulas for computing the optimal
SIAC spline coefficients for the general case including non-uniform knots.
abstract
We explore a class of polynomial tensor-product spline surfaces
on 3-6 polyhedra, whose vertices have valence $n=3$ or $n=6$.
This restriction makes
it possible to exclusively use rational linear transition maps between
the pieces: transitions between the bi-cubic tensor-product spline pieces
are either C
1 or they are G
1 (tangent continuous)
based on one single rational linear reparameterization.
The simplicity of the transition functions yields simple formulas
for a hierarchy of splines on subdivided 3-6 polyhedra.
abstract
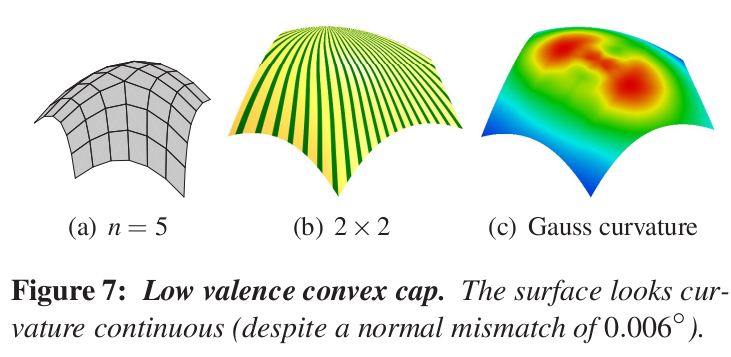
`Class A surface' is a term in the automotive design industry,
describing spline surfaces with aesthetic,
non-oscillating highlight lines.
Tensor-product B-splines of degree bi-3 (bicubic) are routinely used to
generate smooth design surfaces and are often the de facto standard for
downstream processing.
To bridge the gap, this paper explores and gives a concrete suggestion,
how to achieve good highlight line distributions for irregular bi-3
tensor-product patch layout by allowing, along some seams,
a slight mismatch of normals
below the industry-accepted tolerance of one tenth of a degree.
Near the irregularities, the solution can be viewed as transforming
a higher-degree, high-quality formally smooth surface into
a bi-3 spline surface
with few pieces, sacrificing formal smoothness but qualitatively retaining
the shape.
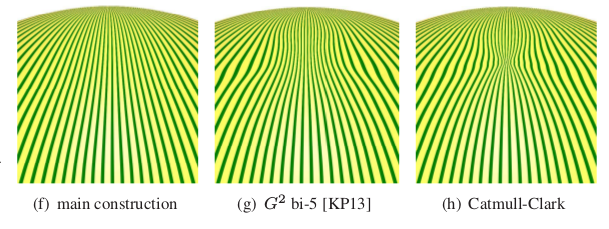
abstract
For many design applications, where multiple primary surface pieces meet,
the distribution of curvature
is more important than formally achieving exact curvature continuity.
For parametric spline surfaces, when constructing a multi-sided
surface cap, we demonstrate a strong link between the uniform
variation of the re-parameterization between (boundary) data of
the joining pieces and a desirable distribution of curvature.
We illustrate this interdependence between parameterization quality and
surface quality by developing a $G^1$ bi-quintic surface cap consisting of
$n$ pieces that smoothly fills holes in a piecewise bi-cubic tensor-product
spline complex. These bi-5 surface caps have arguably better shape
than higher-degree, formally curvature continuous alternatives.
The functional $\mathcal{F}_k$ in (1) should read
$(\partial^i_s\partial^j_tf)^2$
abstract
Geometrically continuous (G
k) constructions naturally
yield families of finite elements for isogeometric analysis
(IGA) that are $C^k$ also for non-tensor-product layout.
This paper describes and analyzes one such concrete $C^1$
geometrically generalized IGA element (short: gIGA element)
that generalizes bi-quadratic splines to quad meshes with
irregularities. The new gIGA element is based on a recently-developed
$G^1$ surface construction that recommends itself by its
a B-spline-like control net, low (least) polynomial degree,
good shape properties and reproduction
of quadratics at irregular (extraordinary) points.
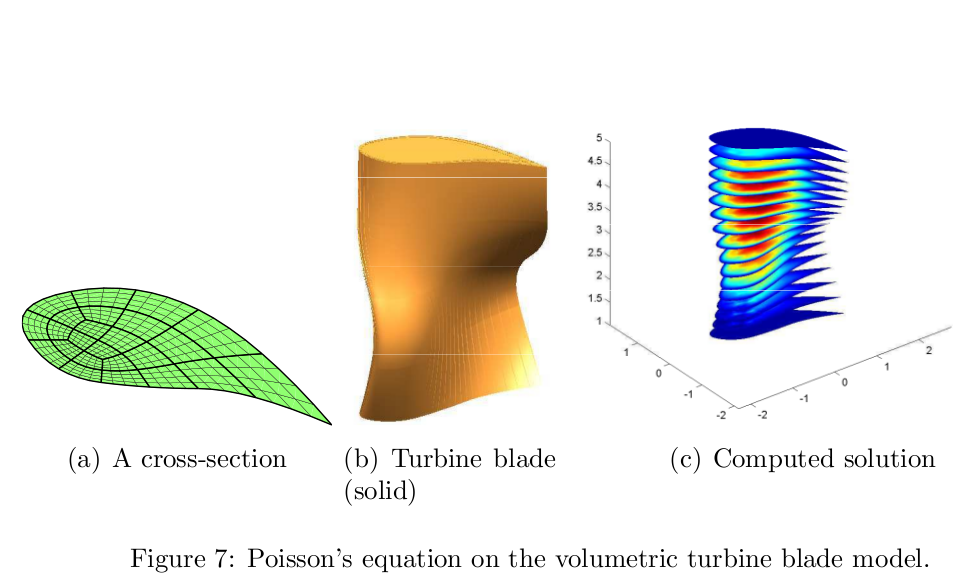
Remarkably, for Poisson's equation on the disk
using interior vertices of valence 3 and symmetric layout,
we observe $O(h^3)$ convergence in the $L^\infty$ norm
for this family of elements.
Numerical experiments confirm the elements to be effective
for solving the trivariate Poisson equation on the solid cylinder,
deformations thereof (a turbine blade), modeling and computing geodesics
on smooth free-form surfaces via the heat equation, for solving
the biharmonic equation on the disk and for Koiter-type thin-shell analysis.
2014
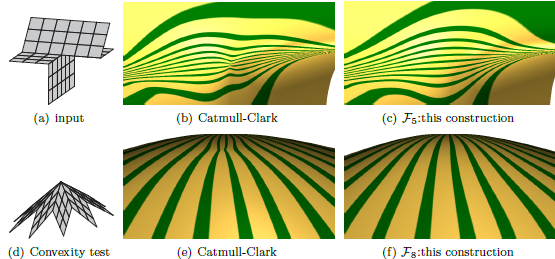
abstract
Biquadratic (bi-2) splines are the simplest choice for converting
a regular quad meshes into smooth tensor-product spline surfaces.
Existing methods for blending three, five or more such
bi-2 spline surfaces using surface caps consisting of pieces of low
polynomial degree
suffer from artifacts ranging from flatness to oscillations.
The new construction, based on reparameterization
of the bi-2 spline data, yields well-distributed highlight lines
for a range of challenging test data.
The construction uses n pieces of bi-3 when n=3,5 or n pieces of
degree bi-4 when n is larger than 5 and applies both to
primal (Catmull-Clark-like) and dual (Doo-Sabin-like) input layouts.
The functional $\mathcal{F}_k$ on page 3 should read
$(\partial^i_s\partial^j_tf)^2$ not
$(\partial^i_s f\partial^j_tf)^2$
p11, Appendix B, formula for $q^1_2$ should read:
..(q^0_1+q^1_1)... (no division by 2)
abstract
Recently, it was shown that a bi-cubic patch complex with
n-sided holes can be completed into a curvature-continuous
surface by n-sided caps of degree bi-5 that offer good and
flexible shape.
This paper further explores the space of n-sided caps
of degree bi-5 but focuses on functionals to set degrees of
freedom and to optimally propagate and average out curvature
from the bi-cubic complex.
The functional $\mathcal{F}_k$ in (1) should read
$(\partial^i_s\partial^j_tf)^2$ not
$(\partial^i_s f\partial^j_tf)^2$
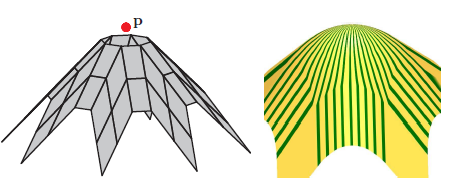
abstract
Shape artifacts, especially for convex input polyhedra,
make Doo and Sabin's generalization of bi-quadratic (bi-2)
subdivision surfaces unattractive for general design.
Rather than tuning the eigenstructure of the subdivision matrix,
we improve shape by adding a point and enriching the refinement rules.
Adding a guiding point can also yield a polar bi-2 subdivision algorithm.
Both the augmented and the polar bi-2 subdivision are complemented by
a new primal bi-2 subdivision scheme. All surfaces are $C^1$
and can be combined.
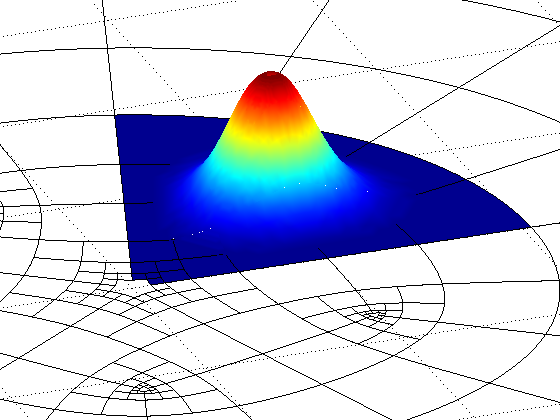
abstract
This paper outlines and qualitatively compares
implementations of seven different methods
for solving Poisson's equation on the disk.
The methods include two classical finite elements, a cotan-formula-based
discrete differential geometry approach and four iso-geometric constructions.
The comparison reveals numerical convergence rates and,
particularly for iso-geometric constructions based on Catmull-Clark elements,
the need to carefully choose quadrature formulas.
The seven methods include two that are new to iso-geometric analysis.
Both new methods yield $O(h^3)$ convergence in the $L^2$ norm,
also when points are included where $n\ne 4$ pieces meet.
One construction is based on a polar, singular parameterization;
the other is a $G^1$ tensor-product construction.
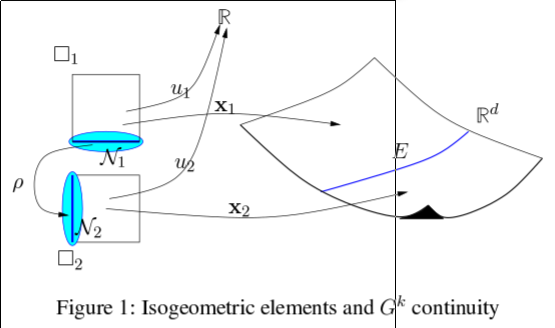
abstract
$G^k$ (geometrically continuous surface) constructions were developed
to create surfaces that are smooth
also at irregular points where, in a quad-mesh, three or more than four
elements come together.
Isogeometric elements were developed to unify the
representation of geometry and of engineering analysis.
We show how matched $G^k$ constructions for geometry and analysis
automatically yield $C^k$ isogeometric elements.
This provides a formal framework for the existing and
any future isogeometric elements based on geometric continuity.

abstract
Current strategies for real-time rendering of trimmed spline surfaces re-approximate the data, pre-process extensively or introduce
visual artifacts. This paper presents a new approach to rendering trimmed spline surfaces that guarantees visual accuracy efficiently,
even under interactive adjustment of trim curves and spline surfaces. The technique achieves robustness and speed by discretizing
at a near-minimal correct resolution based on a tight, low-cost estimate of adaptive domain griding. The algorithm is highly
parallel, with each trim curve writing itself into a slim lookup table. Each surface fragment then makes its trim decision robustly
by comparing its parameters against the sorted table entries. Adding the table-and-test to the rendering pass of a modern graphics
pipeline achieves anti-aliased sub-pixel accuracy at high render-speed, while using little additional memory and fragment shader
effort, even during interactive trim manipulation.
abstract
Splines can be constructed by convolving the indicator function of
a cell whose shifts tessellate R
n. This paper presents simple, geometric
criteria that imply that, for regular shift-invariant tessellations, only a
small subset of such spline families yield nested spaces: primarily the
well-known tensor-product and box splines. Among the many nonrefinable
constructions are hex-splines and their generalization to the
Voronoi cells of non-Cartesian root lattices.
2013
abstract
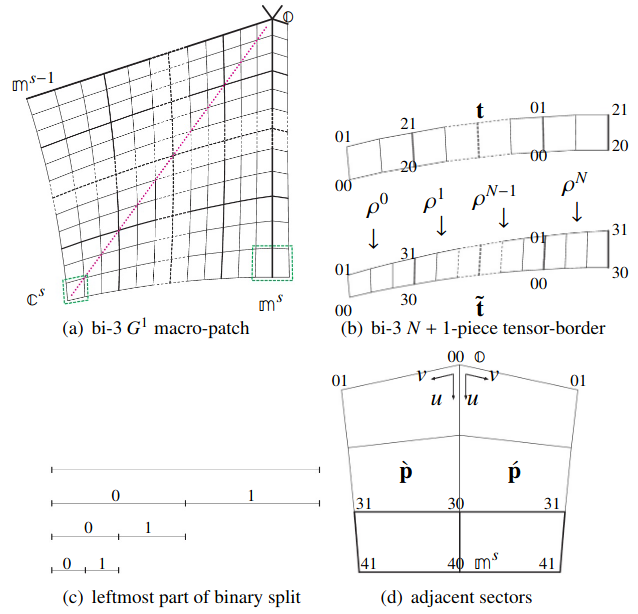
This paper gives a construction to complete, at extraordinary points,
an otherwise bi-cubic spline surface - so that the resulting surface is curvature continuous everywhere. To fill the n-sided gap in the bi-cubic surface,
a cap is constructed from n spline patches, each consisting of 2x2 pieces
of polynomial degree bi-5. Particular care is taken to continue the curvature distribution from the bicubic boundary of the gap into the cap, and
gently average out such propagated curvature in the neighborhood of the
extraordinary point.
The functional $\mathcal{F}_k$ in (16) should read
$(\partial^i_s\partial^j_tf)^2$ not
$(\partial^i_s f\partial^j_tf)^2$

abstract
The definition of a B-spline is extended to unordered knot sequences. The added flexibility implies that
the resulting piecewise polynomials, named U-splines, can be negative and locally linearly dependent. It
is therefore remarkable that linear combinations of U-splines retain many properties of splines in B-spline
form including smoothness, polynomial reproduction, and evaluation by recurrence.
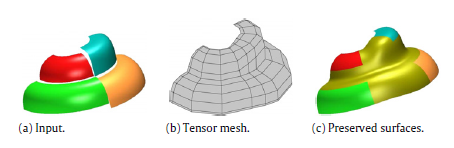
abstract
This paper presents a non-uniform cubic C
2 spline framework that unifies three scenarios for incorporating data from basic curves, such as spirals and conics. In the first scenario, no parameterization of the basic curves is available, only well-spaced samples; in the second, a parameterization is available but cannot be used directly in a spline framework; only in the third scenario can pieces of basic curves be exactly re-represented and included into the spline. In all three cases the output is a cubic C
2 spline suitable for standard CAD downstream processing. A key challenge in constructing the spline is to cope with transitions in the presence of strongly differing curvatures. Here we introduce a new form of curvature-sensitive averaging.
abstract
We present Swarm-NG, a C++ library for the efficient direct integration of many n-body systems using highly-parallel Graphics Processing Unit (GPU), such as NVIDIA's Tesla T10 and M2070 GPUs. While previous studies have demonstrated the benefit of GPUs for n-body simulations with thousands to millions of bodies, Swarm-NG focuses on many few-body systems, e.g., thousands of systems with 3...15 bodies each, as is typical for the study of planetary systems. Swarm-NG parallelizes the simulation, including both the numerical integration of the equations of motion and the evaluation of forces using NVIDIA's "Compute Unified Device Architecture" (CUDA) on the GPU. Swarm-NG includes optimized implementations of 4th order time-symmetrized Hermite integration and mixed variable symplectic integration, as well as several sample codes for other algorithms to illustrate how non-CUDA-savvy users may themselves introduce customized integrators into the Swarm-NG framework. To optimize performance, we analyze the effect of GPU-specific parameters on performance under double precision.
Applications of Swarm-NG include studying the late stages of planet formation, testing the stability of planetary systems and evaluating the goodness-of-fit between many planetary system models and observations of extrasolar planet host stars (e.g., radial velocity, astrometry, transit timing). While Swarm-NG focuses on the parallel integration of many planetary systems,the underlying integrators could be applied to a wide variety of problems that require repeatedly integrating a set of ordinary differential equations many times using different initial conditions and/or parameter values.
2012

abstract
This paper presents new univariate linear non-uniform interpolatory
subdivision constructions that yield high smoothness, C
3 and C
4, and are based
on least-degree spline interpolants. This approach ismotivated by evidence, partly
presented here, that constructions based on high-degree local interpolants fail to
yield satisfactory shape, especially for sparse, non-uniform samples. While this
improves on earlier schemes, a broad consideration of alternatives yields two
technically simpler constructions that result in comparable shape and smoothness:
careful pre-processing of sparse, non-uniform samples and interlaced fitting
with splines of increasing smoothness.We briefly compare these solutions to
recent non-linear interpolatory subdivision schemes
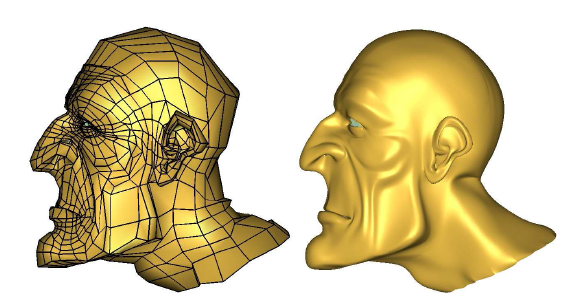
abstract
To efficiently animate and render large models consisting of bi-cubic
patches in real time, we split the rendering into pose-dependent, view-dependent
(Compute-Shader supported) and pure rendering passes. This split avoids recomputation
of curved patches from control structures and minimizes overhead due
to data transfer - and it integrates nicely with a technique to determine a nearminimal
tessellation of the patches while guaranteeing sub-pixel accuracy. Our
DX11 implementation generates and accurately renders 141,000 animated bicubic
patches of a scene in the movie "Elephant's Dream" at more than 300 frames
per second on a 1440x900 screen using one GTX 580 card.
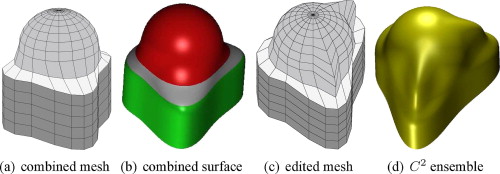
abstract
We show how to automatically join, into one unified spline surface, C
2 tensor-product bi-cubic NURBS and G
2 bi-cubic rational splines. The G
2 splines are capable of exactly representing basic shapes such as (pieces of) quadrics and surfaces of revolution, including tori and cyclides. The main challenge is to transition between the differing forms of continuity. We transform the G
2 splines to splines that are C
2 in homogeneous space. This yields Hermite data for a transitional strip of tensor-product splines of degree (6, 5) that guarantees overall curvature continuity. We also explain the simpler G
1 to C
1 transition. Key to the constructions is the C
2 parameterization of circles in homogeneous space.
abstract
Changing variables is a useful tool that appears in many guises in computer graphics and geometric modeling. Changing the variables allows us to change the way we
traverse a curve or surface, change their derivatives or place or interpret textures and
other properties associated with them. In calculus, changing variables miraculously
converts hard integration problems into simple standard ones and in algebra, seemingly
hard root fnding problems turn into an easy exercises. Even change of coordinates can
be interpreted as a change of variables, albeit linear and therefore not our focus below.
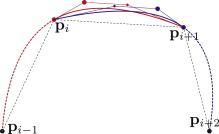
abstract
We present a framework for deriving non-uniform interpolatory subdivision algorithms closely related to non-uniform spline interpolants. Families of symmetric non-uniform interpolatory 2n-point schemes of smoothness C
n-1 are presented for n=2,3,4 and even higher order, as well as a variety of non-uniform 6-point schemes with C
3 continuity.
abstract
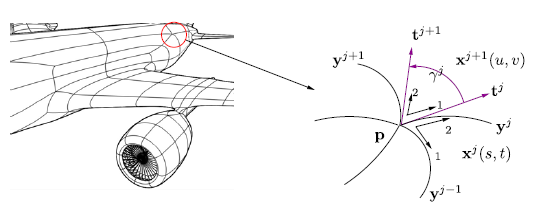
Prescribing a network of curves to be interpolated by a surface model is a standard approach in geometric design. Where n curves meet, even when they afford a common normal direction, they need to satisfy an algebraic condition, called the vertex enclosure constraint, to allow for an interpolating piecewise polynomial C
1 surface. Here we prove the existence of an additional, more subtle constraint that governs the admissibility of curve networks for G
2 interpolation. Additionally, analogous to the first-order case but using the Monge representation of surfaces, we give a sufficient geometric, G
2 Euler condition on the curve network. When satisfied, this condition guarantees existence of an interpolating surface.
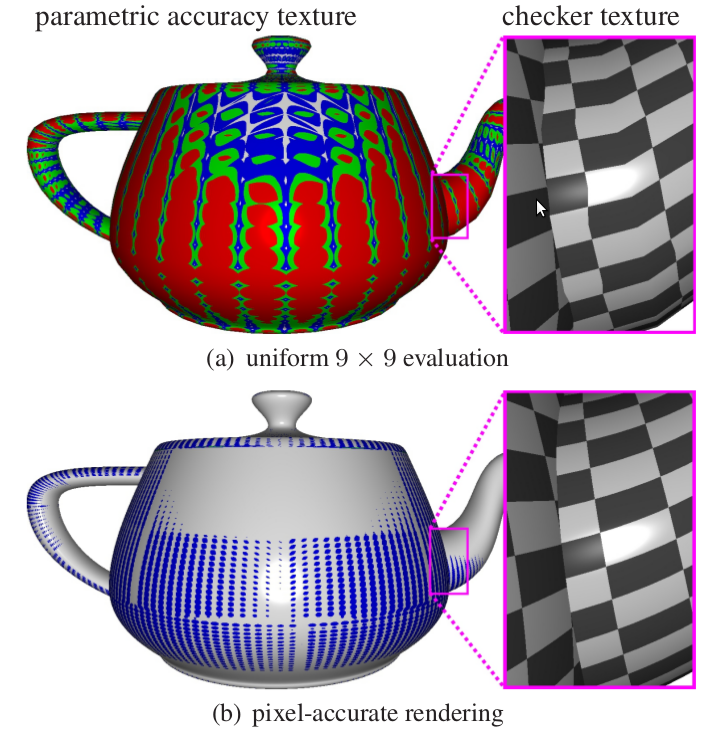
abstract
A curved or higher-order surface, such as spline patch or a Bézier
patch, is rendered pixel-accurate if it displays neither polyhedral artifacts
nor parametric distortion. This paper shows how to set the
evaluation density for a patch just finely enough so that
parametric surfaces render pixel-accurate in the standard graphics pipeline.
The approach uses tight estimates, not of the size under screen projection,
but of the variance under screen projection between
the exact surface and its triangulation. An implementation, using
the GPU tessellation engine, runs at interactive rates comparable to
standard rendering.
(Q by V Gerhard)
Blue in Fig 1:
For some (u,v) the distance || Proj (p(u,v) exact) - Proj( triangle approx) ||_infty \le 1/2 pixel width=height.
So if Proj (p(u,v) exact) hits the center of the pixel, its triangle approximation triggers the same pixel.
The underlying rationale is that if the placement of Proj (p(u,v) exact) is ambiguous between two pixels, eg by being close to the boundary of the pixel square, then triggering the neighbor is legitimate.
(Q by V Gerhard) unclear why the 2nd difference on page 3 has a pre-factor of -d since any fixed factor
depending on d can be absorbed into the table for degree d slefes.
2011

abstract
Root lattices are efficient sampling lattices for reconstructing isotropic signals in arbitrary dimensions, due
to their highly symmetric structure. One root lattice, the Cartesian grid, is almost exclusively used since it
matches the coordinate grid; but it is less efficient than other root lattices. Box-splines, on the other hand,
generalize tensor-product B-splines by allowing non-Cartesian directions. They provide, in any number of
dimensions, higher-order reconstructions of fields, often of higher efficiency than tensored B-splines. But on
non-Cartesian lattices, such as the BCC (Body-Centered Cubic) or the FCC (Face-Centered Cubic) lattice,
only some box-splines and then only up to dimension three have been investigated.
This paper derives and completely characterizes efficient symmetric box-spline reconstruction filters on
all irreducible root lattices that exist in any number of dimensions n = 2 (n = 3 for Dn and Dn* lattices).
In all cases, box-splines are constructed by convolution using the lattice directions, generalizing the known
constructions in two and three variables. For each box-spline, we document the basic properties for computational use: the polynomial degree, the continuity, the linear independence of shifts on the lattice and
optimal quasi-interpolants for fast approximation of fields.

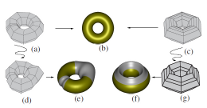
abstract
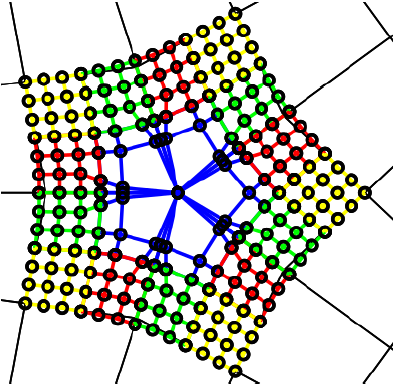
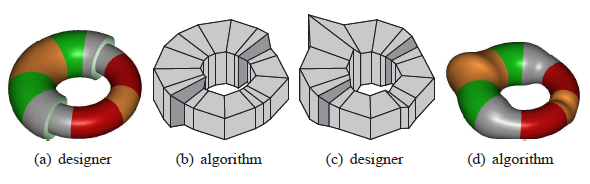
A polar configuration is a triangle fan in a quad-dominant mesh; it allows for many mesh lines to join at a single polar vertex.
This paper shows how a single tensor-product spline of degree (3, 6) can cap a polar configuration with a C
2 surface. By design,
this C
2 polar spline joins C
2 with surrounding bi-3 tensor-product splines and thereby complements algorithms that smoothly cap
star-like, multi-sided regions.
abstract
The paper develops a rational bi-cubic G
2
(curvature continuous) analogue of the non-uniform
polynomial C
2
cubic B-spline paradigm. These rational splines can exactly reproduce
parts of multiple basic shapes, such as cyclides
and quadrics, in one by default smoothly-connected structure.
The versatility of this new tool for processing
exact geometry is illustrated by conceptual design from basic shapes.
typo (found by WeiHua Tong) page 2, col 2,
$c_3 := w^{i-1}_1 W_i w^i_1$ should be $c_3 := w^{i-1}_2 W_i w^i_1$.
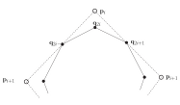
abstract
The promise of modeling by subdivision is to have simple rules that
avoid cumbersome stitching-together of pieces. However, already in one variable,
exactly reproducing a variety of basic shapes, such as conics and spirals, leads to
non-stationary rules that are no longer as simple; and combining these pieces
within the same curve by one set of rules is challenging. Moreover, basis func-
tions, that allow reading off smoothness and computing curvature, are typically
not available. Mimicking subdivision of splines with non-uniform knots allows us
to combine the basic shapes. And to analyze non-uniform subdivision in general,
the literature proposes interpolating the sequence of subdivision control points
by circles. This defines a notion of discrete curvature for interpolatory subdivi-
sion. However, we show that this discrete curvature generically yields misleading
information for non-interpolatory subdivision and typically does not converge,
not even for non-uniform spline subdivision. Analyzing the causes yields three
general approaches for solving or at least mitigating the problem: equalizing pa-
rameterizations, sampling subsequences and a new skip-interpolating subdivision
approach.
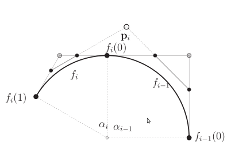
abstract
We develop a class of rational, G
2 -connected splines of
degree 3 that
allow modeling multiple basic shapes, such as segments of conics and cir-
cle arcs in particular, in one structure. This can be used, for example, to
have portions of a control polygon exactly reproduce segments of the shapes
while other portions blend between these primary shapes. We also show
how to reparameterize the splines to obtain parametrically C
2
transitions.
[errata: p.12 p^k_{i-1} should be p^k_i]

abstract
To broaden the use of simulation for teaching, in particular of new procedures and of low-volume procedures, we propose an environment and workflow that allows surgeon-educators create teaching modules. Our challenge is to make the simulation tools accessible, modifiable and sharable by users with moderate computer and VR experience. Our contribution is a workflow that promotes consistency between instructional material and measured criteria and makes the authoring process efficient, both for the surgeon, and for computer scientists supporting the simulation environment.

abstract
We develop a rational biquadratic $G^1$ analogue
of the non-uniform $C^1$ B-spline paradigm.
These $G^1$ splines can exactly reproduce parts of multiple
basic shapes, such as cyclides and quadrics, and combine them into one
smoothly-connected structure.
This enables a design process that starts with basic shapes,
re-represents them in spline form and uses the spline
form to provide shape handles for localized free-form modification
that can preserve, in the large, the initial fair, basic shapes.
[erratum: formula (22) should have a factor 3 -- w^i_{l,1}:=\frac{d_0\mu}{3d_1}]
abstract
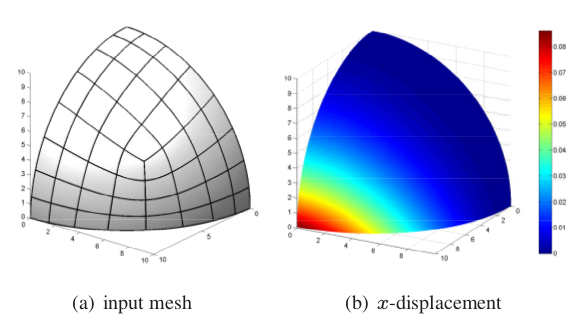
Converting a quadrilateral input mesh into a C
1 surface with one bi-3 tensorproduct
spline patch per facet is a classical challenge. We give explicit local
averaging formulas for the spline control points. Where the quadrilateral mesh
is not regular, the patches have two internal double knots, the least number and
multiplicity to always allow for an unbiased G
1 construction.
[erratum: step 4b: lambdas should have superscript k (as in 3c) - thanks, George]
2010
abstract
We exhibit the essentially unique projective linear (rational linear)
reparameterization for constructing $C^s$ surfaces of genus $g>0$,
from tensor-product splines. Conversely, for quadrilaterals and isolated
vertices of valence 8, we show constructively for s = 1, 2 that
this map yields a projective linear spline space for surfaces of genus greater
or equal to 1. This establishes the reparametrization to be the simplest possible transition map.
abstract
There is an essentially unique projective linear (rational linear)
reparameterization for constructing $C^s$ surfaces from tensor-product splines.
Conversely, for quadrilaterals and isolated vertices of valence 8,
constructions for $s=1,2$ with this map yield a projective
linear spline space for surfaces.
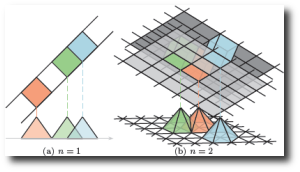
abstract
Sampling and reconstruction of generic multivariate functions
is more efficient on non-Cartesian root lattices,
such as the BCC (Body-Centered Cubic) lattice,
than on the Cartesian lattice. We introduce a new
nx
n generator matrix
A*
that enables,
in
n variables, efficient reconstruction
on the non-Cartesian root lattice
An*
by a symmetric box-spline family
Mr*.
A2* is the hexagonal lattice and
A3* is the BCC lattice. We point out
the similarities and differences of
Mr*
with respect to the popular Cartesian-shifted box-spline family
Mr,
document the main properties of
Mr*
and the partition induced by its knot planes and construct,
in
n variables, the optimal quasi-interpolant of
M2*.
abstract
When interpolating a network of curves to create a C
1 surface
from smooth patches, the network has to satisfy
an algebraic condition, called the vertex enclosure constraint.
We show the existence of an additional constraint
that governs the admissibility of
curve networks for G
2 interpolation by smooth patches.
abstract
Polynomial equation systems arising from real applications often have associated combinatorial information, expressible as graphs and underlying matroids. To simplify the
system and improve its numerical robustness before attempting to solve it with numeric algebraic techniques, solvers can employ graph algorithms to extract substructures sat-
isfying or optimizing various combinatorial properties. When there are underlying matroids, these algorithms can be greedy and efficient. In practice, correct and effective
merging of the outputs of different graph algorithms to simultaneously satisfy their
goals is a key challenge.
This paper merges and improves two highly effective but separate graph-based algorithms that preprocess systems for resolving the relative position and orientation of
a collection of incident rigid bodies. Such collections naturally arise in many situations,
for example in the recombination of decomposed large geometric constraint systems.
Each algorithm selects a subset of incidences, one to optimize algebraic complexity of
a parametrized system, the other to obtain a well-formed system that is robust against
numerical errors. Both algorithms are greedy and can be proven correct by revealing
underlying matroids. The challenge is that the output of the first algorithm is not guaranteed to be extensible to a well-formed system, while the output of the second may not
have optimal algebraic complexity. Here we show how to reconcile the two algorithms by revealing well-behaved maps between the associated matroids.
abstract
Graphs of pairwise incidences between collections of rigid bodies occur in many
practical applications and give rise to large algebraic systems for which all solutions have to be found. Such pairwise incidences have explicit, simple and rational
parametrizations that, in principle, allow us to partially resolve these systems and
arrive at a reduced, parametrized system in terms of the rational parameters. However, the choice of incidences and the partial order of incidence resolution strongly
determine the algebraic complexity of the reduced, parametrized system, measured
primarily in the number of variables and secondarily in the degree of the equations.
Using a pairwise overlap graph, we introduce a combinatorial class of incidence
tree parametrizations for a collection of rigid bodies. Minimizing the algebraic complexity over this class reduces to a purely combinatorial optimization problem that
is a special case of the set cover problem. We quantify the exact improvement of
algebraic complexity obtained by optimization and illustrate the improvement by
examples that can not be solved without optimization.
Since incidence trees represent only a subclass of possible parametrizations, we
characterize when optimizing over this class is useful. That is, we show what properties of standard collections of rigid bodies are necessary for an optimal incidence
tree to have minimal algebraic complexity. For a standard collections of rigid bodies,
the optimal incidence tree parameterization offers lower algebraic complexity than
any other known parameterization.
2009

abstract
We assemble triangular patches of total degree at most eight to form a curvature continuous surface. The construction illustrates
how separation of local shape from representation and formal continuity yields an effective construction paradigm in partly underconstrained
scenarios. The approach localizes the technical challenges and applies the spline approach, i.e. keeping the degree
fixed but increasing the number of pieces, to deal with increased complexity when many patches join at a central point.
abstract
This paper derives strong relations that boundary curves of a smooth
complex of patches have to obey when the patches are computed by local
averaging. These relations restrict the choice of reparameterizations for
geometric continuity.
In particular, when one bicubic tensor-product B-spline patch is associated
with each facet of a quadrilateral mesh with n-valent vertices and
we do not want segments of the boundary curves forced to be linear, then
the relations dictate the minimal number and multiplicity of knots: For
general data, the tensor-product spline patches must have at least two internal
double knots per edge to be able to model a G1-conneced complex
of C1 splines. This lower bound on the complexity of any construction is
proven to be sharp by suitably interpreting an existing surface construction.
That is, we have a tight bound on the complexity of smoothing quad
meshes with bicubic tensor-product B-spline patches.
- Lemma 5, proof: planarity means that
the curve c(u) lies in the tangent plane
since n c(u) = taylor( nc'(0), nc''(0), nc'''(0)) = 0.
- Lemma 5, proof: saddle is symmetric means the surface is
symmetric with respect to the plane through n and c'(0).
- Lemma 6, proof, last statement:
the degree of the derivative along boundary divided by gamma
must be greater or equal 1.
- Thm 1, proof, line 4: (17), respectively (15),
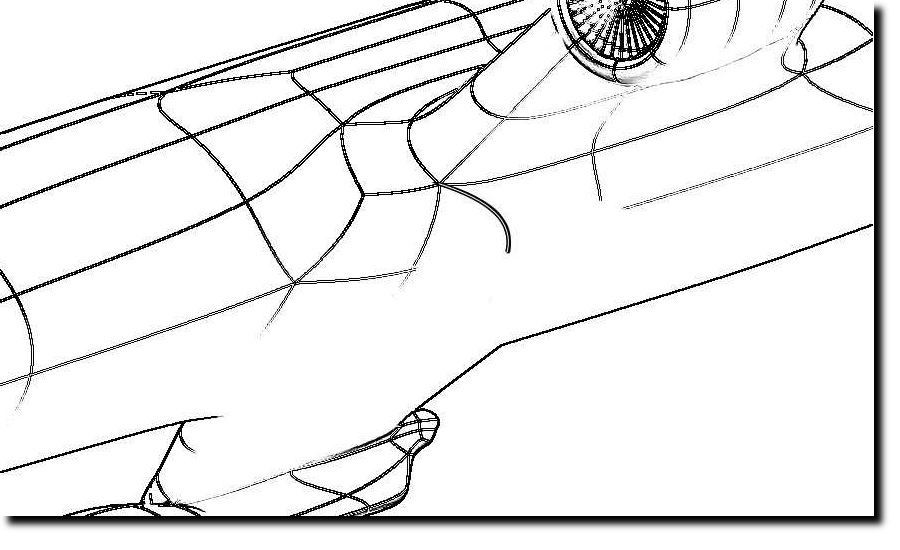
abstract
A key problem when interpolating a network of curves occurs at
vertices: an
algebraic condition called the vertex enclosure constraint
must hold wherever an even number of curves meet. This
paper recasts the constraint in terms of the local geometry of the
curve network. This allows formulating a new
geometric constraint,
related to Euler s Theorem on local curvature, that implies the vertex
enclosure constraint and is equivalent to it where four curve
segments meet without forming an X.

abstract
Lens-shaped surfaces (with vertices of valence 2)
arise for example in automatic quad-remeshing.
Applying standard Catmull-Clark subdivision rules to a
vertex of valence 2, however, does not yield a
C
1 surface in the limit.
When correcting this flaw by adjusting the vertex rule,
we discover a variant whose characteristic ring is
z
2. Since this conformal ring is of
degree bi-2 rather than bi-3,
it allows constructing a subdivision algorithm
that works directly on the control net
and generates C
2 limit surfaces of degree bi-4
for lens-shaped surfaces.
To further improve shape, a number of re-meshing and
re-construction options are discussed indicating that
a careful approach pays off.
Finally, we point out the analogy between characteristic
configurations and the conformal maps
z
4/n, cos z and e
z.
("The original publication is available at www.springerlink.com"
doi 10.1007/s00607-009-0060-9 )
abstract
This course provides an introduction to Approximate Subdivision Surfaces, an overview of the most recent
theoretical results and their implementations on the current and next-generation GPUs, and a demonstration of
these techniques and their applications in the game and movie industries.

abstract
Popular subdivision algorithms like Catmull-Clark and Loop are C
2 almost
everywhere, but suffer from shape artifacts and reduced smoothness exactly
near the so-called "extraordinary vertices" that motivate their use.
Subdivision theory explains that inherently, for standard stationary
subdivision algorithms, curvature-continuity and the ability to model all
quadratic shapes requires a degree of at least bi-6. The existence of a
simple-to-implement C
2 subdivision algorithm generating surfaces of good
shape and piecewise degree bi-3 in the polar setting is therefore a welcome
surprise. This paper presents such an algorithm, the underlying insights,
and a detailed analysis. In bi-3 C
2 polar subdivision the weights depend,
as in standard schemes, only on the valence, but the valence at one central
polar vertex increases to match Catmull-Clark-refinement.

abstract
For use in real-time applications, we present a fast
algorithm for converting a quad mesh to a smooth, piecewise
polynomial surface on the Graphics Processing Unit
(GPU). The surface has well-defined normals everywhere
and closely mimics the shape of CatmullClark subdivision
surfaces. It consists of bicubic splines wherever possible,
and a new class of patchesc-patcheswhere a vertex has
a valence different from 4. The algorithm fits well into parallel
streams so that meshes with 12,000 input quads, of which
60% have one or more non-4-valent vertices, are converted,
evaluated and rendered with 9 x 9 resolution per quad at 50
frames per second. The GPU computations are ordered so
that evaluation avoids pixel dropout.
abstract
We separate the conceptual design and the representation of high quality surfaces by prescribing local shape via guide surfaces
and then sampling these guides with a finite number of tensor-product patches. The paper develops a family of algorithms that allow
trading polynomial degree for smoothness near the extraordinary points where more or fewer than four tensor-product patches
meet. A key contribution are rules for a capping of a multi-sided hole by a small number of polynomial patches. The construction
of highest quality creates first a G1 cap of patches of degree (6, 6) and then perturbs it to yield an exact G2 cap of degree (8, 8).
Since this perturbation is so small that its effect is typically not perceptible even in curvature display, the unperturbed surface of
degree (6, 6) is an excellent alternative. Reducing the degree of the rings to (5, 5), respectively (4, 4), by choice of a different
parameterization, increases the number of G1 transition curves within the cap but does not alter the shape appreciably.
The functional $\mathcal{F}_k$ in Lemma 2 should read
$(\partial^i_s\partial^j_tf)^2$ not
$(\partial^i_s f\partial^j_tf)^2$

abstract
We describe a fully interactive, low-overhead and robust peritoneum representation allowing for probing and cutting. The peritoneum implementation has been tested within a surgical illustration environment.
2008
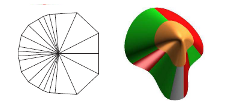
abstract
We present an algorithm for completing a C
2 surface of up to degree bi-6
by capping an n-sided hole with polar layout. The cap consists of n
tensor-product patches, each of degree 6 in the periodic and degree 5 in the radial
direction. To match the polar layout, one edge of these patches is collapsed.
We explore and compare with alternative constructions, based on more pieces or
using total-degree, triangular patches.

Graphs of pairwise incidences between collections of rigid bodies occur in many practical applications and give rise to large algebraic systems for which all solu- tions have to be found. Such pairwise incidences have explicit, simple and rational parametrizations that, in principle, allow us to partially resolve these systems and arrive at a reduced, parametrized system in terms of the rational parameters. How- ever, the choice of incidences and the partial order of incidence resolution strongly determine the algebraic complexity of the reduced, parametrized system measured primarily in the number of variables and secondarily in the degree of the equations.
Using a pairwise overlap graph, we introduce a combinatorial class of incidence tree parametrizations for a collection of rigid bodies. Minimizing the algebraic com- plexity over this class reduces to a purely combinatorial optimization problem that is a special case of the set cover problem. We quantify the exact improvement of algebraic complexity obtained by optimization and illustrate the improvement by examples that can not be solved without optimization.
Since incidence trees represent only a subclass of possible parametrizations, we characterize when optimizing over this class is useful. That is, we show what prop- erties of standard collections of rigid bodies are necessary for an optimal incidence tree to have minimal algebraic complexity. For a standard collections of rigid bodies, the optimal incidence tree parameterization offers lower algebraic complexity than any other known parameterization.

about this book
Since their first appearance in 1974, subdivision algorithms for generating surfaces
of arbitrary topology have gained widespread popularity in computer graphics
and are being evaluated in engineering applications. This development was complemented
by ongoing efforts to develop appropriate mathematical tools for a thorough analysis,
and today, many of the fascinating properties of subdivision are well understood.
This book summarizes the current knowledge on the subject.
It contains both meanwhile classical results as well as brand-new,
unpublished material, such as a new framework for constructing C²-algorithms.
The focus of the book is on the development of a comprehensive mathematical theory,
and less on algorithmic aspects. It is intended to serve researchers and engineers
- both new to the beauty of the subject - as well as experts, academic teachers
and graduate students or, in short, anybody who is interested in the foundations
of this flourishing branch of applied geometry.
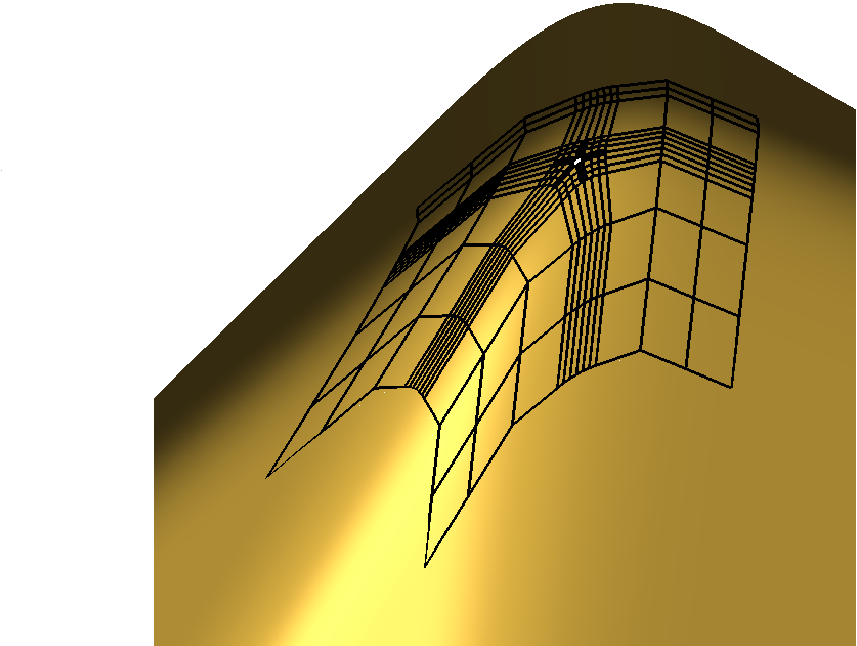
abstract
We introduce a non-uniform subdivision algorithm that
partitions the neighborhood of an extraordinary point in the ratio
σ:1-σ, where σ ; in (0,1).
We call σ the
speed of the non-uniform subdivision
and verify C
1 continuity of the limit surface.
For σ=1/2, the Catmull-Clark algorithm is recovered.
Other speeds are useful to vary the contraction near extraordinary points.
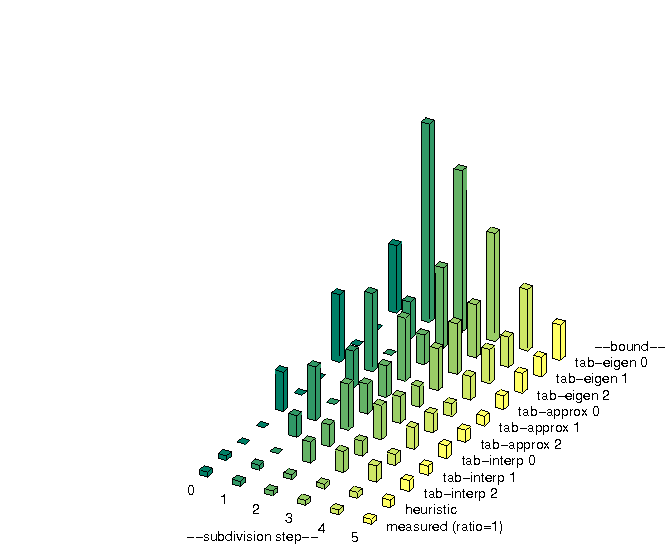
abstract
For standard subdivision algorithms and generic input data,
near an extraordinary point the distance
from the limit surface to the control polyhedron after
m subdivision
steps is shown to decay dominated by the
mth power of
the subsubdominant eigenvalue.
Conversely, for Loop subdivision we exhibit generic input data
so that the Hausdorff distance at the
mth step
is greater or equal to
the
mth power of the subsubdominant eigenvalue.
In practice, it is important to closely predict
the number of subdivision steps necessary so that the control polyhedron
approximates the surface to within a fixed distance.
Based on the above analysis, two such predictions are evaluated.
The first is a popular heuristic that analyzes the distance only
for control points and not for the facets of the control polyhedron.
For a set of test polyhedra this prediction is remarkably close
to the distance verified by a posteriori measurement.
However, a concrete example shows that the prediction is not safe
but can prescribe too few steps.
The second approach is to first locally, per vertex neighborhood,
subdivide the input net and then apply tabulated bounds on the
eigenfunctions of the subdivision algorithm.
This yields always safe predictions that are within one step for a set of
test surface.
("The original publication is available through doi:10.1016/j.jat.2008.10.012)
abstract
This paper gives an overview of two recent techniques for high-quality surface
constructions: polar layout and the guided approach. We demonstrate the chal-
lenge of high-quality surface construction by examples since the notion of surface
quality lacks an overarching theory. A key ingredient of high-quality constructions
is a good layout of the surface pieces. Polar layout simpliï¬es design and is natural
where a high number of pieces meet. A second ingredient is separation of shape
design from surface representation by creating an initial guide shape and leverag-
ing classical approximation-theoretic tools to construct a ï¬nal surface compatible
with industry standards, either as a ï¬nite number of polynomial patches or as a
subdivision process. An example construction generating guided C2 surfaces from
patches of degree bi-3 highlights the power of the approach.
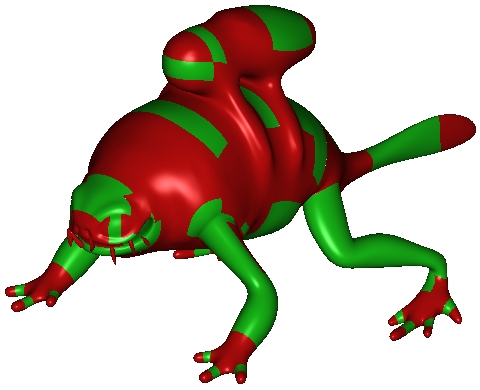
abstract
Determining the least
m such that one
m×
m
bi-cubic macro-patch per quadrilateral offers enough degrees of freedom to
construct a smooth surface by local operations regardless of the vertex
valences is of fundamental interest; and it is of interest for computer
graphics due to the impending ability of GPUs to adaptively evaluate
polynomial patches at animation speeds.
We constructively show that
m = 3 suffices, show that
m = 2
is unlikely to always allow for a localized construction if each
macro-patch is internally parametrically
C 1 and that a
single patch per quad is incompatible with a localized construction. We do
not specify the GPU implementation.

abstract
We introduce and analyze an efficient reconstruction algorithm for FCC-sampled data.
The reconstruction is based on the 6-direction box spline that is naturally
associated with the FCC lattice and shares the continuity and
approximation order of the triquadratic B-spline.
We observe less aliasing for generic level sets and derive special techniques
to attain the higher evaluation efficiency promised by the lower degree and
smaller stencil-size of the 6-direction box spline over the triquadratic B-spline.
» The work was supported in part by NSF grant CCF-0728797
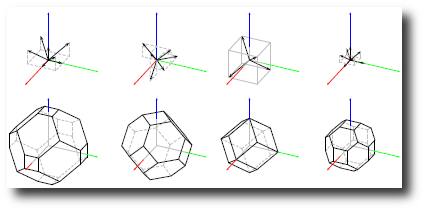
abstract
Due to their highly symmetric structure, in arbitrary dimensions root lattices are
considered as efficient sampling lattices for reconstructing isotropic signals. Among the
root lattices the Cartesian lattice is widely used since it naturally matches the Cartesian
coordinates. However, in low dimensions, non-Cartesian root lattices have been shown to
be more efficient sampling lattices.
For reconstruction we turn to a specific class of multivariate splines. Multivariate
splines have played an important role in approximation theory. In particular, box-splines,
a generalization of univariate uniform B-splines to multiple variables, can be used to
approximate continuous fields sampled on the Cartesian lattice in arbitrary dimensions.
Box-splines on non-Cartesian lattices have been used limited to at most dimension three.
This dissertation investigates symmetric box-splines as reconstruction filters on root
lattices (including the Cartesian lattice) in arbitrary dimensions. These box-splines are
constructed by leveraging the directions inherent in each lattice. For each box-spline, its
degree, continuity and the linear independence of the sequence of its shifts are established.
Quasi-interpolants for quick approximation of continuous fields are derived. We show that
some of the box-splines agree with known constructions in low dimensions.
For fast and exact evaluation, we show that and how the splines can be efficiently
evaluated via their BB(Bernstein-Bézier)-forms. This relies on a technique to compute
their exact (rational) BB-coefficients. As an application, volumetric data reconstruction on
the FCC (Face-Centered Cubic) lattice is implemented and compared with reconstruction
on the Cartesian lattice.


abstract
To repeatedly evaluate linear combinations of box-splines in a fast
and stable way, in particular along knot planes, the box-spline is converted
to and tabulated as piecewise polynomial in BB-form (Bernstein-
Bézier-form). We show that the BB-coefficients can be derived and stored
as integers plus a rational scale factor and derive a hash table for efficiently
accessing the polynomial pieces. This preprocessing, the resulting
evaluation algorithm and use in a widely-used ray-tracing package are illustrated
for splines based on two trivariate box-splines: the 7-directional
box-spline on the Cartesian lattice and the 6-directional box-spline on the
Face-Centered Cubic lattice.
The work was supported in part by NSF grant CCF-0728797.
»
MATLAB® package & movies download page
- In equation (7), ‘-1’ in M-1 should not be in bold face.
- In equation (7), all three ks should be italic: k.
- In the proof of Lemma 1, 2nd paragraph 3rd line, ζ' (lower zeta prime) and Ξ' (upper xi prime) both should be the same symbol Z (upper zeta).
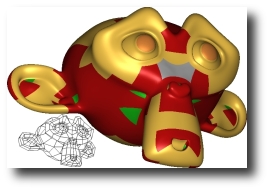
abstract
Polyhedral meshes consisting of triangles, quads, and pentagons
and polar configurations cover all major sampling and modeling scenarios.
We give an algorithm for efficient local, parallel conversion of
such meshes to an everywhere smooth surface consisting of low-degree polynomial pieces.
Quadrilateral facets with 4-valent vertices are ‘regular’ and are mapped to
bi-cubic patches so that adjacent bi-cubics join
C² as for
cubic tensor-product splines. The algorithm can be implemented in the vertex
and geometry shaders of the GPU pipeline and does not use the fragment shader.
Its implementation in DirectX 10 achieves conversion plus rendering at 659 frames
per second with 42.5 million triangles per second on input of a model of 1,300
facets of which 60% are not regular.
The work was supported in part by NSF grant CCF-0728797
abstract
Surface constructions of polynomial degree (3,3) come in four
flavours that complement each other: one pair extends the
subdivision paradigm, the other the NURBS patch approach to
free-form modeling.
The first pair, Catmull-Clark and Polar subdivision generalize
bi-cubic subdivision: While Catmull-Clark subdivision is more
suitable where few facets join, Polar subdivision nicely models
regions where many facets join as when capping extruded
features. We show how to easily combine (the meshes of) these
two generalizations of bi-cubic spline subdivision.
The second pair of surface constructions with a finite number of
patches consists of PCCM for layouts where Catmull-Clark would
apply and a singularly parameterized NURBS patch for polar
layout. A novel analysis shows the latter to yield a $C^1$
surface with bounded curvatures.
abstract
We present a fast algorithm for converting quad meshes on the GPU to smooth surfaces.
Meshes with 12,000 input quads, of which 60% have one or more non-4-valent vertices,
are converted, evaluated and rendered with 9×9 resolution per quad at 50 frames per second.
The conversion reproduces bi-cubic splines wherever possible and closely mimics
the shape of the Catmull-Clark subdivision surface by c-patches where a vertex
has a valence different from 4. The smooth surface is piecewise polynomial and
has well-defined normals everywhere. The evaluation avoids pixel dropout.
The work was supported in part by NSF grant CCF-0728797.
abstract
We convert any quad manifold mesh into an at least
C¹ surface
consisting of bi-cubic tensor-product splines with localized perturbations of
degree bi-5 near non-4-valent vertices. There is one polynomial piece per quad facet,
regardless of the valence of the vertices. Particular care is taken to derive
simple formulas so that the surfaces are computed efficiently in parallel and
match up precisely when computed independently on the GPU.
The work was supported in part by NSF grant CCF-0728797.

abstract
Modeling soft tissue for surgery simulation is a challenging task due to the complex way
that the tissue can deform and interact with virtual surgical tools manipulated by user.
One soft tissue that is ubiquitous but often not modeled, is fatty tissue. Here we present
a novel fatty tissue model based on the mass-spring system on the Graphics Processing Unit (GPU)
as part of our Toolkit for Illustration of Procedures in Surgery (TIPS).
The user can interact with the fatty tissue in real time via a handheld haptic stylus that
represents a virtual surgical tool in TIPS environment. The currently available interactions are palpation, grasp, and cut.
abstract
Following (Karciauskas and Peters, “Concentric Tesselation Maps and Curvature Continuous Guided Surfaces”)
below, we analyze surfaces arising as an infinite sequence of guided
C² surface rings.
However, here we focus on constructions of too low a degree to be curvature continuous also
at the extraordinary point. To characterize shape and smoothness of such surfaces,
we track a sequence of quadratic functions anchored in a fixed coordinate system.
These ‘anchored osculating quadratics’ are easily computed in terms of
determinants of surface derivatives. Convergence of the sequence of quadratics certifies curvature continuity.
Otherwise, the range of the curvatures of the limit quadratics gives a measure of deviation from curvature continuity.
2007
abstract
We complete and bring together two pairs of surface constructions
that use polynomial pieces of degree (3,3) to associate a smooth surface
with a mesh with polar structures. The two pairs complement each other in that
one extends the Catmull-Clark subdivision-modeling paradigm, the other
the PCCM NURBS patch approach to free-form modeling. In the process,
we also show the curvature boundedness of certain singularly
parameterized finite splines using a novel perspective.
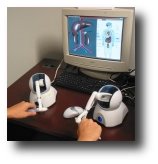
abstract
Good surgical training depends greatly on case experiences that have been difficult
to model in software since current training technology does not provide the flexibility
to teach and practice uncommon procedures, or to adjust a training scenario on the fly.
The TIPS kit aims to overcome these limitations. To the expert, it presents visual and haptic tools
that make illustrating procedures easy and can model unusual anatomic variations.
For a non-specialist, it provides a locally customized learning environment and
repeated practice in a safe environment. We used the toolkit to illustrate removal of the adrenal gland.
abstract
We have developed a computer based simulation process which allows
a surgical expert to create a customized operative environment.
This virtual environment, the Toolkit for Illustration of Procedures in Surgery (3D TIPS),
is deployed on a low-cost computer system and requires minimal training for the programmer.
The learner can be engaged in training immediately and the educator can modify the system
and annotate the procedure to highlight specific points using video clips, operative images,
and the like.
A laparoscopic adrenalectomy is presented as a proof of concept in the accompanying article.
abstract
The guided spline approach to surface construction separates surface design
and surface representation by constructing local guide surfaces and
sampling these by splines of moderate degree. This paper explains
a construction based on tessellating the domain into V-shaped regions
so that the resulting
C² surfaces have
G²
transitions across the boundaries of the V-shapes and consist of
tensor-product splines of degree (6,6) with patches of degree (4,4) forming a central cap.
The functional $\mathcal{F}_k$ page 7 (1) should read
$(\partial^i_s\partial^j_tf)^2$ not
$(\partial^i_s f\partial^j_tf)^2$
abstract
A multi-sided hole in a surface can be filled by a sequence of nested,
smoothly joined surface rings. We show how to generate such a sequence so that
(i) the resulting surface is
C² (also in the limit),
(ii) the rings consist of standard splines of moderate degree and
(iii) the hole filling closely follows the shape of and replaces a guide surface
whose good shape is desirable, but whose representation is undesirable.
To preserve the shape, the guided rings sample position and higher-order derivatives
of the guide surface at parameters defined and weighted by a concentric tesselating map.
A concentric tesselating map maps the domains of n patches to an annulus in
ℜ²
that joins smoothly with a λ-scaled copy of itself, 0 < λ < 1.
The union of λ
m-scaled copies parametrizes a neighborhood of the origin
and the map thereby relates the domains of the surface rings to that of the guide.
The approach applies to and is implemented for a variety of splines and layouts
including the three-direction box spline (with Δ-sprocket, e.g. Loop layout,
at extraordinary points), tensor-product splines (quad-sprocket layout, e.g. Catmull-Clark),
and polar layout. For different patch types and layout, the approach results in
curvature continuous surfaces of degree less or equal 8, less or equal to (6,6),
and as low as (4,3) if we allow geometric continuity.
abstract
We describe and analyze a subdivision scheme that generalizes bicubic spline subdivision
to control nets with polar structure. Such control nets appear naturally for surfaces
with the combinatorial structure of objects of revolution and at points of high valence
when combined with Catmull-Clark subdivision. The resulting surfaces are
C²
except at isolated extraordinary points where the surface is
C¹ and the curvature is bounded.
abstract
We describe the structure and general properties of surfaces with polar layout.
Polar layout is particularly suitable for high valences and is,
for example, generated by a new class of subdivision schemes.
This note gives an high level view of surfaces with polar structure and does not analyze particular schemes.
abstract
For planar spline curves and bivariate box-spline functions,
the cone of normals of a polynomial spline piece is enclosed
by the cone of normals of its spline control polyhedron.
This note collects some concrete examples to show that
this is not true for subdivision surfaces, both at extraordinary points and in the regular,
box-spline setting. A larger set, the cross products of families
of control net edges, has to be considered.
2006
abstract
The rapid development and deployment of novel laparoscopic instruments
present the surgical educator and trainee with a significant challenge.
Several useful instruments have been particularly difficult to teach the novice.
We have developed a platform that allows the combination of the actual instrument
handle with a virtual re-creation of the instrument tip. We chose the Autosuture™
Endo Stitch™ device as the prototypical instrument because it satisfies
our subjective experience of “useful, but hard to teach.”
A software package was developed to support the re-creation of the needle
and suture that accompany the device. The apparatus has haptic capabilities
and collision detection so that the needle driver is “aware” of suture and instrument contact.
The developed virtual environment allows re-creation of the necessary motion to simulate
the instrument, the trainee can use the actual instrument handle, and the system can be
altered to accommodate other instruments.
abstract
Real-time, plausible visual and haptic feedback of deformable objects without shape artifacts
is important in surgical simulation environments to avoid distracting the user.
We propose to leverage highly parallel stream processing, available on the newest
generation graphics cards, to increase the level of both visual and haptic fidelity.
We implemented this as part of the University of Florida's haptic surgical authoring kit.
abstract
By separating shape design from representation,
the guided approach to surface construction (Karciauskas and Peters,
“Concentric tessellation maps and guided surface rings”)
allows to routinely construct everywhere
C² surfaces
with (infinite) subdivision structure. This paper shows a finite guided
C² surface construction of degree (6,6), albeit with many pieces,
that preserves the good algebraic properties of the construction of
k-th order
smooth surfaces of least degree in (Peters, “
C² free-form surfaces of degree (3,5)“),
while avoiding geometric degeneration.
The functional $\mathcal{F}_k$ on page 7 (c) should read
$(\partial^i_s\partial^j_tf)^2$ not
$(\partial^i_s f\partial^j_tf)^2$
abstract
We describe a subdivision scheme that acts on control nodes that
each carry a vector of values. Each vector defines partial derivatives,
referred to as jets in the following and subdivision computes new jets
from old jets. By default, the jets are automatically initialized from a design mesh.
While the approach applies more generally, we consider here only a restricted class of design meshes,
consisting of extraordinary nodes surrounded by triangles and otherwise quadrilaterals
with interior nodes of valence four. This polar mesh structure is appropriate for surfaces
with the combinatorial structure of objects of revolution and for high valences.
The resulting surfaces are curvature continuous with good curvature distribution
near extraordinary points. Near extraordinary points the surfaces are piecewise polynomial
of degree (6,5), away they are standard bicubic splines.
abstract
To support real-time computation with large, possibly evolving point clouds
and range data, we fit a trimmed uniform tensor-product spline function from one direction.
The graph of this spline serves as a surrogate for the cloud, closely following
the data safely in that, according to user choice, the data are always ‘below’
or ‘above’ when viewed in the fitting direction. That is, the point cloud
is guaranteed to be completely covered from that direction and can be sandwiched between
two matching spline surfaces if required. This yields both a data reduction since only
the spline control points need to be further processed and defines a continuous surface
in lieu of the isolated measurement points.
abstract
Characterizing the linear and local linear independence of the functions
that span a linear space is a key task if the space is to be used computationally.
Given the control net, the spanning functions of one spatial coordinate
of a generalized subdivision surface are called nodal functions.
They are the limit, under subdivision, of associating the value one with one node
and zero with all others. No characterization of independence of nodal functions
has not been published to date, even for the two most popular generalized subdivision algorithms,
Catmull-Clark subdivision and Loop's subdivision. This paper provides a road map
for the verification of linear and local linear independence of generalized subdivision functions.
It proves the conjectured global independence of the nodal functions of both algorithms;
disproves local linear independence (for higher valences); and establishes linear independence
on every surface region corresponding to a facet of the control net. Subtle exceptions,
even to global independence, underscore the need for a detailed analysis to provide
a sound basis for a number of recently developed computational approaches.
2005
abstract
This paper summarizes the structure and analysis of subdivision surfaces
and characterizes the inherent similarities and differences to parametric spline surfaces.
Besides presenting well known results in a unified way, we introduce new ideas
for analyzing schemes with a linearly dependent generating system,
and a significantly simplified test for the injectivity of the characteristic map.


abstract
In
“A realtime GPU subdivision kernel” (SIGGRAPH 2005), Shiue et
al. showed that, in principle, all major features of subdivision algorithms
can be realized in the framework of highly parallel stream processing.
Shiue et al. tested the approach by implementing Catmull-Clark
subdivision, with semi-smooth creases and global boundaries, in
programmable graphics hardware, at near realtime speed.
Here, we report on the challenges when adapting the approach to
Loop subdivision.
abstract
Automatically generated or laser-scanned surfaces typically exhibit
large clusters with a uniform pattern. To take advantage of the regularity
within clusters and still be able to edit without decompression,
we developed a two-level data structure that uses an enumeration
by orbits and an individually adjustable stencil to flexibly describe connectivity.
The structure is concise for storing mesh connectivity; efficient for random access,
interactive editing, and recursive refinement; and it is flexible by supporting
a large assortment of connectity patterns and subdivision schemes.
abstract
The Flexible Subdivision Library, FSL, is a policy-based C++ template library
for refining geometric meshes. The library is generic and only requires
that the underlying mesh data structure provide Euler operations,
iterators and circulators, and a point type. Any specific subdivision strategy
is efficiently realized by a user-defined geometry policy.
abstract
By organizing the control mesh of subdivision in texture memory
so that irregularities occur strictly inside independently refinable fragment mesh,
all major features of subdivision algorithms can be realized in the framework of
highly parallel stream processing. Our implementation of Catmull-Clark subdivision
as a GPU kernel in programmable graphics hardware can model features like
semi-smooth creases and global boundaries; and a simplified version achieves
near-realtime depth-five re-evaluation of moderate-sized subdivision meshes.
The approach is easily adapted to other refinement patterns, such as Loop,
Doo-Sabin or √3 and it allows for postprocessing with additional shaders.
abstract
Curvature continuous surfaces with subdivision structure are constructed
by higher-order sampling of a piecewise polynomial guide surface,
at positions defined and derivatives weighted by a special,
scalable reparametrization. Two variants are developed.
One variant applies to the conventional sprocket subdivision layout,
say of Catmull-Clark subdivision, i.e. nested rings consisting of
N copies of L-shaped segments with three patches.
The curvature continuous surfaces are of degree (6,6).
A second variant, called polar guided subdivision,
is particularly suitable for high valences
N
and to cap cylindrical structures. It yields curvature
continuous surfaces of degree (4,3). Additionally,
we discuss a scheme that samples with increasing density to generate
a
C² surface of piecewise degree (3,3).
Curvature continuity is verified by showing convergence of anchored osculation paraboloids.
abstract
This paper characterizes when the normals of a spline curve
or spline surface lie in the more easily computed cone of
the normals of the segments of the spline control net.
abstract
A sequence of mesh manipulations that preserves the Euler invariant
is called an Euler encoding. We propose new, efficient Euler encodings
for primal and dual mesh refinement. The implementations are analyzed
and compared to array-based, connectivity-free refinement and
to reconstruction of the refined mesh.
abstract
A tight estimate on the maximum distance between a subdivision surface
and its linear approximation is introduced to guide
adaptive subdivision with guaranteed accuracy.
2004
abstract
Modern geometric constraint solvers use combinatorial graph algorithms
to recursively decompose the system of polynomial constraint equations
into generically rigid subsystems and then solve the overall system by solving subsystems,
from the leave nodes up, to be able to access any and all solutions.
Since the overall algebraic complexity of the solution task is dominated
by the size of the largest subsystem, such graph algorithms attempt
to minimize the fan-in at each recombination stage.
Recently, we found that, especially for 3D geometric constraint systems,
a further graph-theoretic optimization of each rigid subsystem is both possible,
and often necessary to solve wellconstrained systems: a minimum spanning tree
characterizes what partial eliminations should be performed before
a generic algebraic or numeric solver is called.
The weights and therefore the elimination hierarchy defined by this
minimum spanning tree computation depend crucially on the representation of the constraints.
This paper presents a simple representation that turns many previously untractable systems
into easy exercises. We trace a solution family for varying constraint data.
abstract
4-3 direction subdivision combines quad and triangle meshes.
On quad submeshes it applies a 4-direction alternative
to Catmull-Clark subdivision and on triangle submeshes
a modification of Loop's scheme. Remarkably, 4-3 surfaces
can be proven to be
C¹ and have bounded curvature everywhere.
In regular mesh regions, they are
C² and correspond
to two closely-related box-splines of degree four.
The box-spline in quad regions has a smaller stencil than
Catmull-Clark and defines the unique scheme with a 3 by 3 stencil
that can model constant features without ripples both aligned
with the quad grid and diagonal to it. From a theoretical point of view,
4-3 subdivision near extraordinary points is remarkable in that
the eigenstructure of the local subdivision matrix is easy to determine
and a complete analysis is possible. Without tweaking the rules artificially
to force a specific spectrum, the leading eigenvalues ordered by modulus of
all local subdivision matrices are 1, ½, ½, ¼ where the multiplicity
of the eigenvalue ¼ depends on the valence of the extraordinary point
and the number of quads surrounding it. This implies equal refinement of the mesh,
regardless of the number of neighbors of a mesh node.
abstract
Accurate and robust interference detection and ray-tracing
of subdivision surfaces requires safe linear approximations.
Approximation of the limit surface by the subdivided
control polyhedron can be both inaccurate and,
due to the exponential growth of the number of facets, costly.
This paper shows how a standard intersection hierarchy,
such as an OBB tree, can be made safe and efficient for
subdivision surface interference detection. The key is to construct,
on the fly, optimally placed facets, whose spherical offsets tightly
enclose the limit surface. The spherically offset facets can be
locally subdivided and they can be efficiently intersected based on
standard triangle-triangle interference detection.
abstract
Given a polygonal channel between obstacles in the plane or in space,
we present an algorithm for generating a parametric spline curve
with few pieces that traverses the channel and stays inside.
While the problem without emphasis on few pieces has trivial solutions,
the problem for a limited budget of pieces represents a nonlinear
and continuous (‘infinite’) feasibility problem.
Using tight, two-sided, piecewise linear bounds on the potential solution curves,
we reformulate the problem as a finite, linear feasibility problem whose solution,
by standard linear programming techniques, is a solution of the channel fitting problem.
The algorithm allows the user to specify the degree and smoothness of the solution curve
and to minimize an objective function, for example, to approximately minimize
the curvature of the spline. We describe in detail how to formulate and solve the problem,
as well as the problem of fitting parallel curves, for a spline in Bernstein-Bézier form.
Marcelo Siqueira noticed:
Sec 4.1 (1st para) should read $D_i b^p_\mu$ (subscripted).
(published: second variable misses a "b")
Page 146 (1st col Fig 10):
switched $e_s^p$ and $e_{s-1}^p$ in the right drawing.
Constraint (3c): should it be $\text{normal}_j^p$
(with $j$ one of $c-1$ or $c+1$) or
$\text{normal}_c^p$ in the inequality? (cf (3a) and (3b))
(2) counting: open and closed curve differ
(3c) counting: should be (or no 2^\text{dim}?)
$K := 2^\text{dim} 2 (n_e + 1)$ inequalities per e-piece
where the middle 2 refers to the number of caps per tunnel?
This would yield $KN$ inequalities total.
abstract
Given a planar spline curve and local tolerances,
a matched pair of polygons is computed that encloses the curve
and whose width (distance between corresponding break points)
is below the tolerances. This is the simplest instance of
a subdividable linear efficient variety enclosure, short sleve.
We develop general criteria, that certify correctness of a global,
polygonal enclosure built from a sequence of individual bounding boxes
by extending and intersecting their edges.
These criteria prove correctness of the sleve construction.
Marcelo Siqueira found the following (non-lethal) typos:
Fig. 13(b) certificate (2) may not be satisfied.
Fig. 14(b) caption should read
"q2 does not intersect the interior of $\square_2$"
Sec. 7 (beginning) could be mis-interpreted as stating that certificate (3)
is "sufficient" for the conclusion of Lemma 7.1.
(the hypothesis of Lemma 7.1 makes clear that cerificates (1)-(3)
together form a "sufficient" condition).
Page 624: should be "we negate".
Def 5.1 (last sentence): if and only if $d_\mu(v)$ is of one sign
abstract
We provide asymptotic expansions for the fundamental forms,
the Weingarten map, the principal curvatures, and the principal directions
of surfaces generated by linear stationary subdivision schemes.
Further, we define the central surface. The central surface is
a spline ring that captures basic shape properties of the surface
in the vicinity of an extraordinary vertex. Relating the shape properties
to the spectrum of the subdivision matrix via the discrete
Fourier transform yields conditions for the construction of
high-quality subdivision schemes. In particular, the subsub-dominant
eigenvalue should be triple and correspond to the Fourier blocks
with indices 0,2 and
n-2 of the subdivision matrix.
abstract
For subdivision surfaces, it is important to characterize local shape near flat spots
and points where the surface is not twice continuously differentiable.
Applying general principles derived in
"[Peters, Reif] Shape Characterization... - Basic Principles",
this paper characterizes shape near such points for the subdivision schemes
devised by Catmull and Clark and by Loop. For generic input data, both schemes
fail to converge to the hyperbolic or elliptic limit shape suggested
by the geometry of the input mesh: the limit shape is a function of
the valence of the extraordinary node rather than the mesh geometry.
We characterize the meshes for which the schemes behave as expected
and indicate modifications of the schemes that prevent convergence
to the wrong shape. We also introduce a type of chart that,
for a specific scheme, can help a designer to detect early
when a mesh will lead to undesirable curvature behavior.
abstract
On the construction of high-quality surfaces...
2003
abstract
Bézier or B-spline control meshes are quintessential CAGD tools
because they link piecewise linear and curved geometry by providing a linear,
refinable approximation that exaggerates features and is, up to reparametrization,
in 1-1 correspondence with the curved geometry. However, for a given budget
of line segments, Bézier and B-spline control meshes are usually
far from the ‘nearest’ piecewise linear approximant to the curved geometry.
Subdividable Linear Efficient Function Enclosures, short SLEFEs
(pronounced like sleeves), aim at sandwiching the curved geometry as tightly as possible.
This paper illustrates how to derive SLEFEs, lists the literature on SLEFEs,
discusses SLEFEs for rational functions and tensor-products and analyzes
the improvement of SLEFEs under refinement. The average of the upper and
lower SLEFE bounds is called mid-structure. Mid-structures come close
to being the ‘nearest’ piecewise linear approximant
while retaining the 1-1 correspondence and the computational efficiency of control meshes.
abstract
An algorithm is presented for approximating a rational multi-sided M-patch
by a
C² spline surface. The motivation is that
the multi-sided patch can be assumed to have good shape
but is in nonstandard representation or of too high a degree.
The algorithm generates a finite approximation of the M-patch,
by a sequence of patches of bidegree (5,5) capped off by patches of bidegree (11,11)
surrounding the extraordinary point. The philosophy of the approach is
(i) that intricate reparametrizations are permissible if they improve
the surface parametrization since they can be precomputed and thereby
do not reduce the time efficiency at runtime; and
(ii) that high patch degree is acceptable if the shape is controlled by a guiding patch.
abstract
We show how a future graphics processor unit (GPU),
enhanced with random read and write to video memory,
can represent, refine and adjust complex meshes arising in modeling,
simulation and animation. To leverage SIMD parallelism,
a general model based on the mesh atlas is developed and
a particular implementation without adjacency pointers
is proposed in which primal, binary refinement of, possibly mixed,
quadrilateral and triangular meshes of arbitrary topological genus,
as well as their traversal is supported by user-transparent
programmable graphics hardware. Adjustment, such as subdivision smoothing rules,
is realized as user programmable mesh shader routines.
Attributes are generic and can be defined in the graphics application
by binding them to one of several general addressing mechanisms.
abstract
This paper surveys a new, computationally efficient technique
for linearizing curved spline geometry, bounding such geometry from one side
and constructing curved spline geometry that stays to one side of a barrier
or inside a given channel. Combined with a narrow error bound,
these reapproximations tightly couple linear and nonlinear representations
and allow them to be substituted when reasoning about the other.
For example, a subdividable linear efficient variety enclosure
(SLEVE, pronounced like Steve) of a composite spline surface is
a pair of matched triangulations that sandwich a surface and
may be used for interference checks. The average of the SLEVE components,
the mid-structure, is a good max-norm linearization and,
similar to a control polytope, has a well-defined,
associated curved geometry representation. Finally, the ability
to fit paths through given channels or keep surfaces near
but outside forbidden regions, allows extending many techniques
of linear computational geometry to the curved, nonlinear realm.
abstract
subdividable linear efficient function enclosures
(slefes) and more
2002
abstract
Subdividable linear efficient function enclosures (Slefes) provide,
at low cost, a piecewise linear pair of upper and lower bounds
ƒ
+, ƒ
-, that sandwich a function ƒ
on a given interval: ƒ
- ≤ ƒ ≤ ƒ
+.
In practice, these bounds are observed to be very tight.
This paper addresses the question just how close to optimal,
in the max-norm, the slefe construction actually is.
Specifically, we compare the width (ƒ
+)-(ƒ
-)
of the slefe to the narrowest possible piecewise linear enclosure of
ƒ when ƒ is a univariate cubic polynomial.
abstract
This paper surveys the key achievements and outstanding challenges of
constructing smooth surfaces for geometric design.
The focus here is on explicit methods in parametric form.
In particular, recent insights into the curvature magnitude
and distribution of surfaces generated by existing algorithms,
based on generalized subdivision and on splines, are illustrated
and corresponding research questions are formulated.
These challenges motivate the search for alternative
approaches to multi-sided patch constructions.
abstract
Optimized Refinable Surface Enclosures are tight, two-sided enclosures
of composite spline surfaces. This paper shows how to construct
the two hulls whose matched triangle pairs sandwich a given nonlinear,
curved surface consisting of tensor-product Bezier patches.
The hulls are cheap to compute with linear effort per patch.
The width of the enclosure, i,e. the distance between inner and
outer hull can be easily measured because the maxima are taken
on at the vertices. The width shrinks quadratically under subdivision
(uniform knot insertion). Uses of surface envelopes are easier point
classification and intersection testing and an improved rule for
approximately rendering curved surfaces as triangulations with a known error bound.
abstract
This chapter covers geometric continuity with emphasis on
a constructive definition for piecewise parametrized surfaces.
The examples in Section 1 show the need for a notion of continuity different
from the direct matching of Taylor expansions used to define
the continuity of piecewise functions. Section 2 defines geometric continuity
for parametric curves, and for surfaces, first along edges, then around points,
and finally for a whole complex of patches which is called a
Gk
free-form surface spline. Here
Gk characterizes a relation
between specific maps while
Ck continuity is a property of
the resulting surface. The composition constraint on reparametrizations
and the vertex-enclosure constraints are highlighted. Section 3 covers
alternative definitions based on geometric invariants, global and regional
reparametrization and briefly discusses geometric continuity in the context of
implicit representations and generalized subdivision. Section 4 explains the
generic construction of
Gk free-form surface splines
and points to some low degree constructions. The chapter closes with
a listing of additional literature.
abstract
This paper presents a technique for modeling curvature continuous free-form surfaces
of unrestricted patch layout from patches of maximal degree
d+2,
d>0
by 3 with the flexibility of degree
d,
C² splines at extraordinary points
2001
abstract
For a stationary, affine invariant, symmetric, linear and local subdivision scheme
that is
C² apart from the extraordinary point the curvature is bounded
if the square of the subdominant eigenvalue equals the subsubdominant eigenvalue.
This paper gives a technique for quickly establishing an interval to which
the curvature is confined at the extraordinary point. The approach factors
the work into precomputed intervals that depend only on the scheme
and a mesh-specific component. In many cases the intervals are tight enough
to be used as a test of shape-faithfulness of the given subdivision scheme;
i.e. if the limit surface in the neighborhood of the extraordinary point
of the subdivision scheme is consistent with the geometry implied by the input mesh.
abstract
To improve the visual quality of existing triangle-based art in real-time entertainment,
such as computer games, we propose replacing flat triangles with curved patches
and higher-order normal variation. At the hardware level, based only
on the three vertices and three vertex normals of a given flat triangle,
we substitute the geometry of a three-sided cubic Bézier patch for
the triangle's flat geometry, and a quadratically varying normal for Gouraud shading.
These curved point-normal triangles, or PN triangles, require minimal or
no change to existing authoring tools and hardware designs while providing a smoother,
though not necessarily everywhere tangent continuous, silhouette and more organic shapes.
Curved PN Quads
Tech report
2008

( The analogue of PN triangles for quadrilateral patches.)
abstract
(Old title: Envelopes for tensor product polynomials) An an optimized refinable enclosure
is a two-sided approximation of a uni- or multivariate function
b in
B
by a pair of typically simpler functions
b-,
b+
in
H not equal to
B such that
b- ≤
b ≤
b+
over the domain of of interest. Enclosures are optimized by minimizing the width
max
U b+ -
b- and refined
by enlarging the space
H. This paper develops a framework
for efficiently computing enclosures for multivariate polynomials and,
in particular, derives piecewise bilinear enclosures for bivariate polynomials
in tensor-product Bézier form. Runtime computation of enclosures
consists of looking up
s < dim
B pre-optimized enclosures
and linearly combining them with the second differences of
b.
The width of these enclosures scales by a factor ¼ under midpoint subdivision.
abstract
The problem, given a polynomial
p of degree
d+1 find a best 2-norm approximation
over the unit interval from polynomials of degree
d, is shown to be equivalent to
the problem of finding the best
l2 approximation of the vector of BB coefficients
of
p from the vector of BB coefficients of once degree-raised polynomials of degree
d.
Moreover, analogous to repeated degree-reduction in
L2,
l2 degree reduction
one step at a time from degree
n to degree
d.





























 talk
talk










 talk
talk























 talk (2013)
talk (2013)

 talk (2013)
talk (2013)


 talk
talk






















 Talk
Talk  .
.  Code
patch_tess_pass.cs.glsl(line 297): change to
float max_[]_panel_width[3] = {0,0,0};
Code
patch_tess_pass.cs.glsl(line 297): change to
float max_[]_panel_width[3] = {0,0,0};



































 talk
talk









 [Errata
updated 2009-02-24]
[Errata
updated 2009-02-24]
 (9.2MB)
(9.2MB)





































 Talk Slefe
Talk Slefe  Talk Mid
Talk Mid 










 ( The analogue of PN triangles for quadrilateral patches.)
( The analogue of PN triangles for quadrilateral patches.)

 bsbounds
bsbounds