Research and Software
The newest research results appear under Publications .
PnSiga
Solving PDEs on Manifolds videoPnS3
. use freecad for igesiPASS using OpenGL 4
An OpenGL 4 implementation of the interactive Pixel-Accurate Shading of Surfaces (iPASS) algorithm.Blender free-form modeling
Semi-structure splinesToolkit for Illustration of Procedures in Surgery
TIPSVascularVR
Polyhedral Splines
Swarm-NG: Discovery of extra-solar planets using CUDA
Project documentation | Source CodePublication: Dindar, S., E.B. Ford, M. Juric, Y.I. Yeo, J. Gao, A.C. Boley, B. Nelson, J. Peters Swarm-NG: A CUDA Library for Parallel n-body Integrations with focus on Simulations of Planetary Systems , New Astronomy, Volumes 23-24, October 2013, Pages 6-18 DOI: 10.1016/j.newast.2013.01.002 arXiv:1208.1157 [astro-ph.EP].
Box-splines and applications
M. KimConstraint Solving and Configuration Spaces
M. Sitharam videoTri/Quad/Pent Surface Patch Construction and Rendering on the GPU
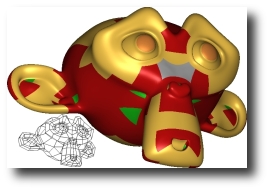 |
As an alternative to mesh refinement, a quad-dominant control mesh is
converted directly to polynomial patches that join smoothly. Our
two-pass GPU algorithm addresses meshes with adjacent extraordinary
vertices, triangles, pentagons, and polar configurations. The first pass
constructs the Bezier patches of the final surface using the vertex and
geometry shader, and the second pass evaluates and renders these patches
after sending in a pre-tessellated domain. The source code is freely
available for educational purposes and has been tested on the following.
(pdf) (movie 9.2MB) (source code, updated 2009-02-24) |
A Realtime GPU Subdivision Kernel
| By organizing the control mesh of subdivision in texture memory so that irregularities occur strictly inside independently refinable fragment mesh, all major features of subdivision algorithms can be realized in the framework of highly parallel stream processing. Our implementation of Catmull-Clark subdivision as a GPU kernel in programmable graphics hardware can model features like semi-smooth creases and global boundaries; and a simplified version achieves near-realtime depth-five re-evaluation of moderate-sized subdivision meshes. The approach is easily adapted to other refinement patterns, such as Loop, Doo-Sabin or sqrt3 and it allows for postprocessing with additional shaders. (pdf) (quicktime movie) |
4-3 Direction Subdivision
 |
4-3 subdivision is an alternative to Catmull-Clark subdivision on quadrilateral nets and a modification of Loop's scheme for triangulations, plus a simple transition rule. In regular mesh regions, 4-3 surfaces are C2 (otherwise C1) and generalize two closely-related quartic box-splines. The quad-component of 4-3 has a smaller stencil than Catmull-Clark and is the unique scheme with a 3 x 3 stencil that can model constant features, aligned with the quad grid or diagonal to it, without ripples. (pdf) |
Subdividable Linear Maximum-norm Enclosure (SubLiME)
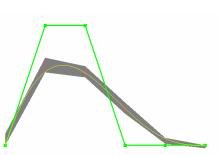 |
Subdividable linear efficient function enclosures (Slefes) provide, at low cost, a piecewise linear pair of upper and lower bounds f^+, f^-, that sandwich a function f on a given interval: f^- <= f <= f^+. These bounds are observed to be very tight. See papers: [Univariate B\'ezier], [Multivariate], [uniform B-Spline], [Optimality] and download the SubLiME package for [Linux/Unix], [Windows] (Version 1.1, updated June 22th 2003) |
Mesh Mutation in Programmable Graphics Hardware
 |
We show how a future graphics or visual processor unit, enhanced with random read and write to video memory, can represent, refine and adjust complex meshes arising in modeling, simulation and animation. To leverage SIMD parallelism, a general model based on the mesh atlas is developed and a particular implementation without pointers is proposed in which primal, binary refinement of, possibly mixed, quadrilateral and triangular meshes of arbitrary topological genus, as well as their traversal is supported by user-transparent programmable graphics hardware. Adjustment, such as subdivision smoothing rules, is realized as user-programmable mesh shader routines. Attributes are generic and can be defined in the graphics application by binding them to one of several general addressing mechanisms. (pdf) |
Patching Catmull-Clark Meshes
 |
PCCM transformation creates maximally large, smoothly joining Nurbs patches of order 4 from Catmull-Clark subdivision meshes. It can be applied after any of the first subdivision steps and creates patches that are maximally large in the sense that one patch corresponds to one quadrilateral facet of the initial, coarsest quadrilateral mesh before subdivision. The patches join $C^2$ almost everywhere and with tangent continuity in the immediate neighborhood of extraordinary mesh nodes, matching the global smoothness of Catmull-Clark limit surfaces. More... |
Surface Splines
 |
C1 surface splines represent smooth manifolds that can be
embedded smoothly or non-smoothly into Rn. The connectivity
allows for arbitrary patch layout and the blend ratios for local control
over the distribution of curvature. In particular, sharp features can be
modeled in the same framework by local, intuitive choice of these blend
ratios.
More... The GMOD title page shows a surface spline. We implemented a minimal, portable C-implementation of Surface splines without major data structure overhead (Read the papers in particular Pcp2Nurb): OpenGL code and VRML output |
Box-Spline Based CSG Blends
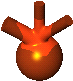 |
To blend implicitly defined constructive solid geometry surfaces, we
are using the zero set of a spline in three variables. The resulting blend
surface is generically curvature continuous, of algebraic degree four independent
of the number of surfaces joined, and supports both point classification
and efficient rendering.
More... |
The Artesano immediate modeler
 |
Artesano provides an intuitive interface to modeling complex
surfaces. It is based on deforming surfaces with virtual tools rather than
by modifying mathematical quantities such as control points or blend ratios.
The virtual tools mimic the tools a designer uses for modeling in clay.
It is primarily intended for the first steps in a design process, where
creativity is more important than exactness in the mathematical sense.
Even though, the models produced are guaranteed to be smooth and can be
easily exported into general CAD-packages.
It uses the SurfLab's geometry library using an Open Inventor frontend. A port to WIN32 platforms exists. |
||
 |
Objects and images created with Artesano | ||
Real time moment computations
 |
Efficient and exact calculation of the moments of objects enclosed
by a free-form surface for animation or design. Since the moments, like
the volume, can be computed rapidly, it is possible to solve inverse problems
as, for example, determining the fill-height of a given volume of liquid
in a container in real-time.
Show me the movie QuickTime movie (260k bytes) |
The Topological House

|
Homotopy illustrating a piecewise linear immersion of the sphere in
3-space such that its complement is connected. The representation interpolating
the sphere and the final house has to be capable of continuously increasing
the curvature, resulting in sharp edges in the limit.
|
SurfLab's geometry library
|
The library consists of a collection of data structures, routines, and
programs to define and manipulate the geometry of Surface Splines
and other parametric representations.
The geometry library is composed of several modules of C++, Maple, and Matlab code. The C++ modules work for SGI IRIX 5.3 and Windows NT. BezierView A small program to visualize Bezier patches and their curvatures. |
Last modified
10:34:18 AM, Thu Nov 07, 2024