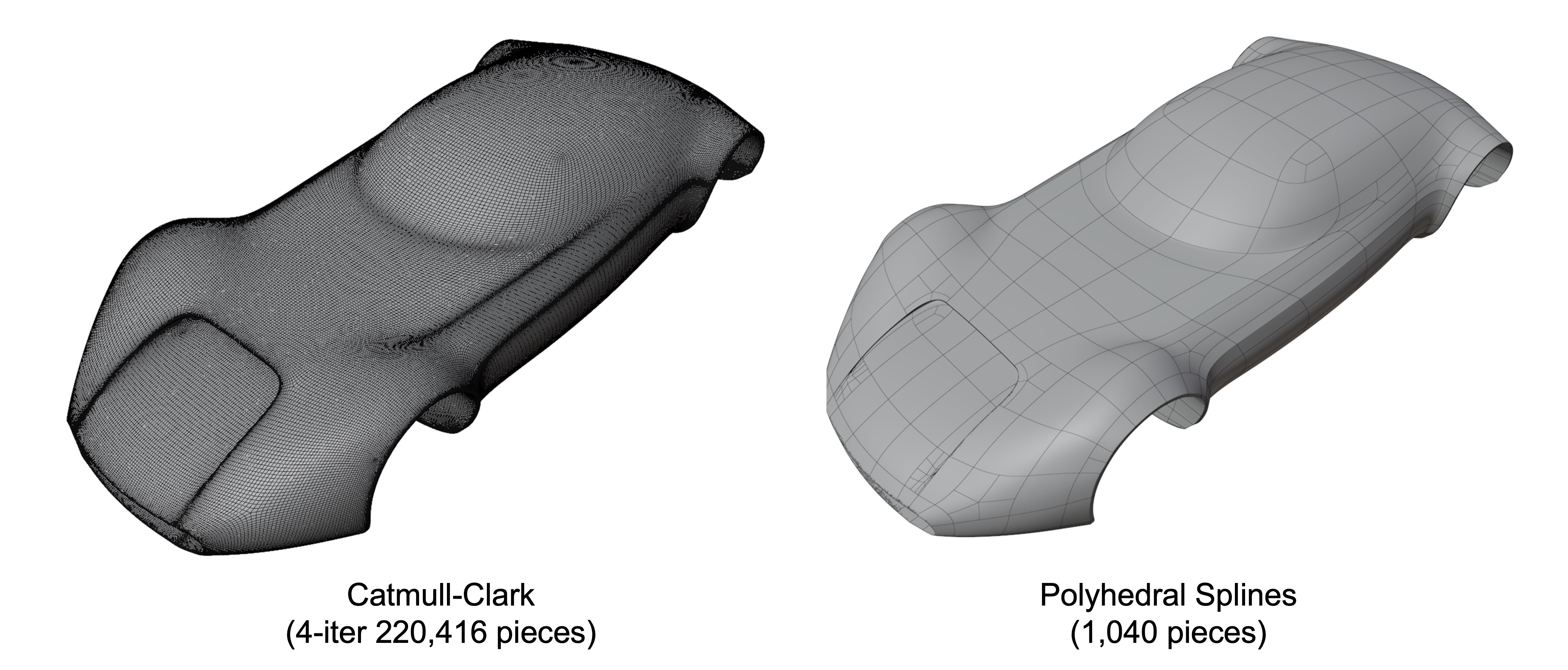
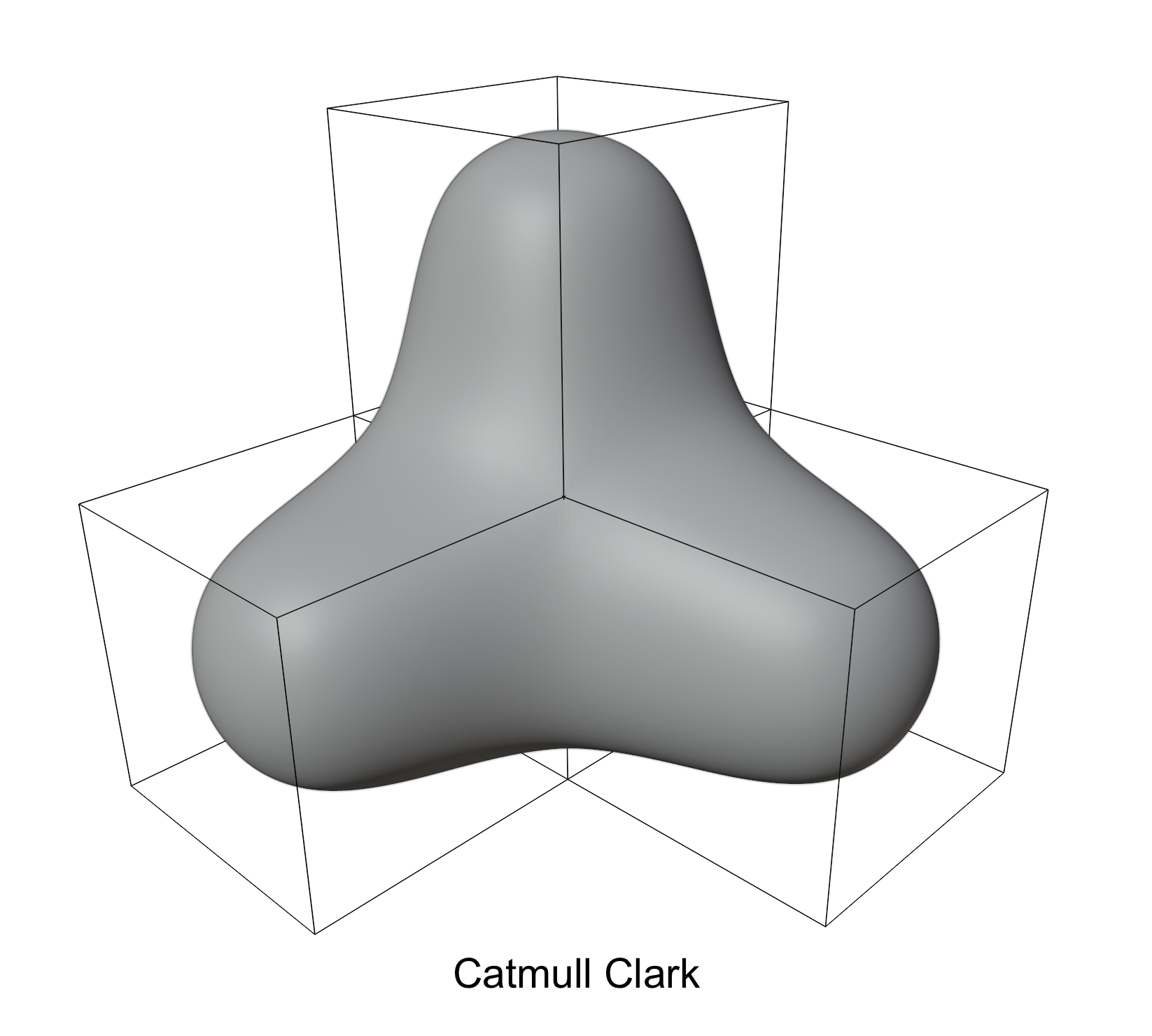
Introduction

Polyhedral-net splines (PnS2) convert a polyhedral-net into piecewise Bezier patches of degree no more than bi-3

Top: input mesh, Bottom: B-spline patches generated by Polyhedral-net splines (Gray: regular Bi-2, Green: extraordinary point, Cyan: T0, Yellow: T1)

 

Features

1. Smooth surfaces without subdividing the mesh.

   

2. Easy, exact computation of moments, e.g. volume, center of mass, axes of inertia, …

3. Preserves the polyhedral character of the input
   (Polyhedral-net splines (PnS2) generalize bi-2, bi-quadratic, splines. Bi-2 splines are by default less smooth than bi-3 splines, and curvature changes more sharply.)
4. _{PnS3, a different package, generalizes bi-3 C2 splines}

   

   

 

Installation

• Download the executable (Windows, Mac, Ubuntu).
• Alternatively build from Source.

Usage

• Input: polyhedral-net in .obj file format
• Output: BB-patches of degree at most bi-3 in .bv, .igs, .step file format

For .bv output, see BView file introduction.

For .igs or .step output, see e.g. freeCAD

Execution

For UNIX-based systems

build/PolyhedralSplines [options] <input>

For Windows (PowerShell)

build\Debug\PolyhedralSplines.exe [options] <input>

Options

• -h, --help: Show this help message and exit.
• -d, --DEGREE_RAISE: Raise degree-2 patches to degree 3.
• -f, --FORMAT <enum>: Output format: bv, igs, step (default: bv).

Positional arguments

• input<string>: Input file (required). Example: mesh.obj

Usage Examples

• build/PolyhedralSplines mesh.obj
• build/PolyhedralSplines -d mesh.obj
• build/PolyhedralSplines -f igs mesh.obj
• build/PolyhedralSplines -d -f igs mesh.obj

Web Demo

Try out an interactive, in-browser visualization of polyhedral splines. You can upload your own .obj files as control mesh and download .bv, .igs or .step.

Launch the live demo

Python Library

The Python library provide a programmatic interface to generate and export polyhedral spline surfaces.

• API Reference - full documentation of classes and functions.
• Sample Jupyter Notebook - step-by-step tutorial demonstrating common workflows on google colab.

C# Library

The C# library provide a programmatic interface to generate and export polyhedral spline surfaces.

• API Reference - full documentation of classes and functions.

Implemented algorithms

1. Karčiauskas, K., & Peters, J. (2015). Smooth multi-sided blending of biquadratic splines. Computers & Graphics, 46, 172-185.
2. Karčiauskas, K., & Peters, J. (2020). Smooth polar caps for locally quad-dominant meshes. Computer Aided Geometric Design, 81, 101908.
3. Karčiauskas, K., & Peters, J. (2020). Low degree splines for locally quad-dominant meshes. Computer Aided Geometric Design, 83, 101934.

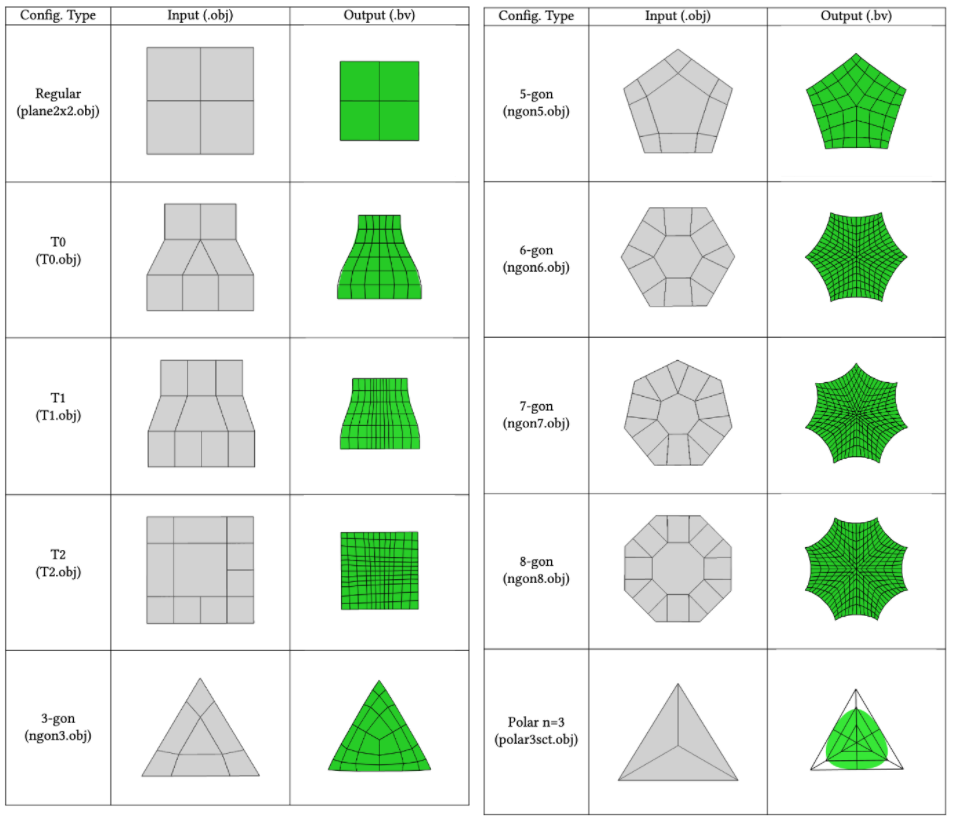
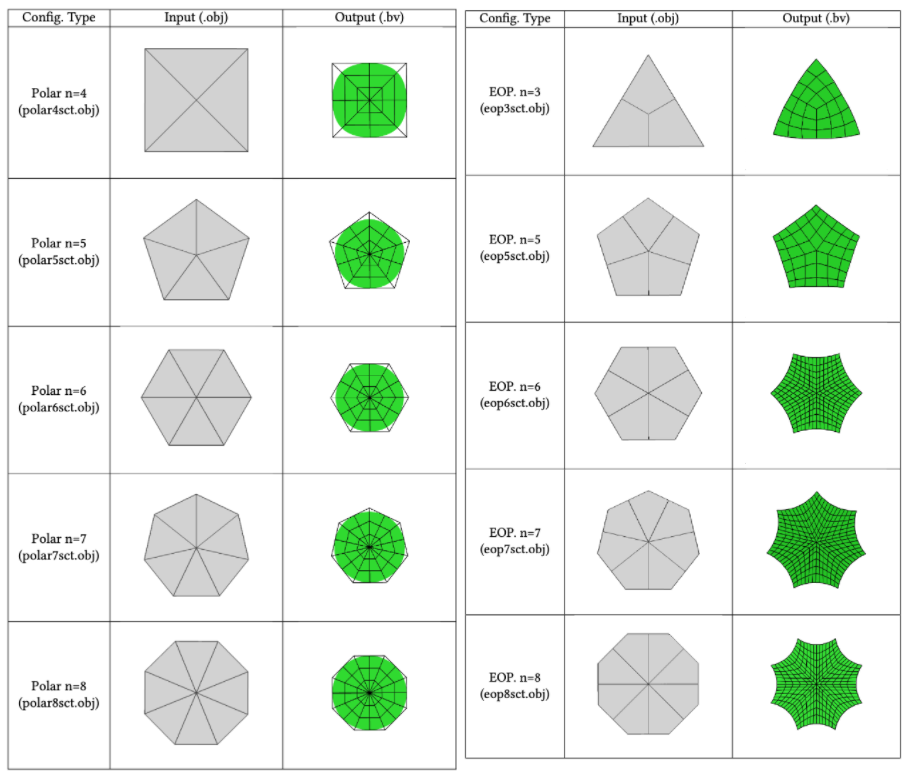
Allowable configurations

The single subdivision step will be applied automatically if any unsupported configuration is detected.

(gray: submesh / green: tensor-product splines)