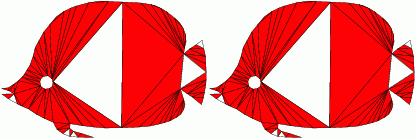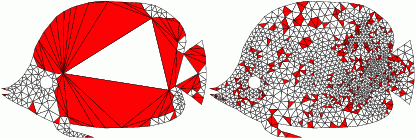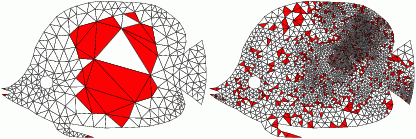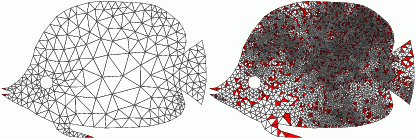
|
aCute A premium quality meshing software. |
|
Implemented and licensed at the University of Florida, Gainesville
Partially funded by an NSF CAREER Award and an NSF Regular Grant
Contact: Alper Ungor, CISE Department, University of Florida, Gainesville, FL, 32611 ungoratcisedotufldotedu
The main ideas for aCute have been discussed in the following research papers:
Abstract: We propose two novel ideas to improve the performance of Delaunay refinement algorithms which are used for computing quality triangulations. The first idea is an effective use of the Voronoi diagram and unifies previously suggested Steiner point insertion schemes (circumcenter, sink, off-center) together with a new strategy. The second idea is the integration of a new local smoothing strategy into the refinement process. These lead to two new versions of Delaunay refinement, where the second is simply an extension of the first. For a given input domain and a constraint angle $\alpha$, Delaunay refinement algorithms aim to compute triangulations that have all angles at least $\alpha$. The original Delaunay refinement algorithm of Ruppert is proven to terminate with size-optimal quality triangulations for $\alpha \le 20.7^\circ$. In practice, the original and the consequent Delaunay refinement algorithms generally work for $\alpha \le 34^\circ$ and fail to terminate for larger constraint angles. Our algorithms provide the same theoretical guarantees as the previous Delaunay refinement algorithms. The second of the proposed algorithms generally terminates for constraint angles up to $42^\circ$. Experiments also indicate that our algorithm computes significantly (about by a factor of two) smaller triangulations than the output of the previous Delaunay refinement algorithms. Moreover, the new algorithms are experimentally shown to outperform the previous algorithms even in the existence of additional constraints, such as the maximum area triangle constraint which is commonly used for computing uniform triangulations.
Abstract: We propose a heuristic method for computing Steiner triangulations without small and large angles. Given a two-dimensional domain, a minimum angle constraint alpha and a maximum angle constraint gamma, our method computes a triangulation of the domain such that all angles are in the interval [alpha, gamma]. Previously known Steiner triangulation methods generally consider a lower bound alpha only, and claim a trivial upper bound (gamma = 180 - 2*alpha). Available software work for alpha as high as 34 degrees (implying a gamma value of 112 degrees), However, they fail consistently whenever larger alpha and/or smaller gamma values are desired. Experimental study shows that the proposed method works for alpha as high as 41 degrees, and gamma as low as 81 degrees. This is also the first software for computing high quality acute and non-obtuse triangulations of complex geometry.
Note that, aCute also relies on the previous research cited by the Jonathan Shewchuk's Triangle research credit page. Please refer to that page for more information on Delaunay refinement algorithm.