aCute
A premium quality meshing software.
|
|
Implemented and licensed at the University of Florida, Gainesville
Partially funded by an NSF CAREER Award and an NSF Regular Grant
Contact: Alper Ungor, CISE Department, University of Florida, Gainesville, FL, 32611 ungoratcisedotufldotedu
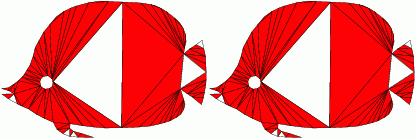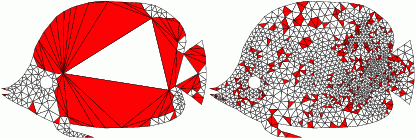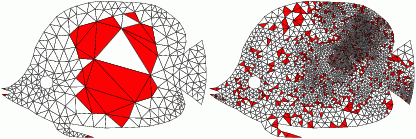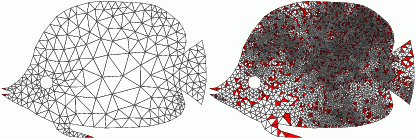
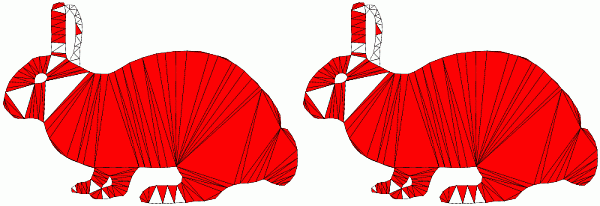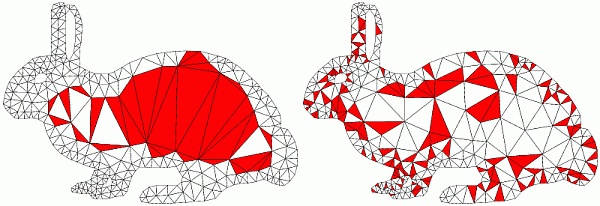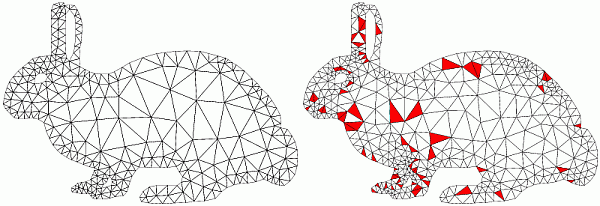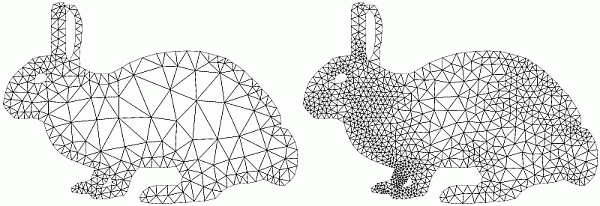
Algorithmic Approach Comparison
aCute
| Triangle
|
| Our software employs an advancing front approach,
inserts locally optimal Steiner points, first near the boundary of the domain.
|
The original Triangle software employed
Ruppert's circumcenter insertion algorithm which is not an advancing front approach.
|
| Below you see an execution of each algorithm/software interrupted
after certain number of Steiner point insertion (specified). Desired smallest angle is
34 degrees. Bad triangles are marked red. Initial triangulations are the same.
|
The Idea
Here, a brief discussion about the idea which helps us to generate premium quality triangulations by using Delaunay refinement as the basis
.
Locally Optimal Steiner Points
Given an ordered pair of points (p,q) in the input domain, consider the circle that
goes through p and q, of radius |pq| / (2*sin(alpha)), whose center is on the
right side of the directed edge pq. The disk bounded by this circle is called the
petal of pq, denoted by petal(pq). Based on this definition, we choose from four different types of points to insert a Steiner point which can be simply shown as follows:
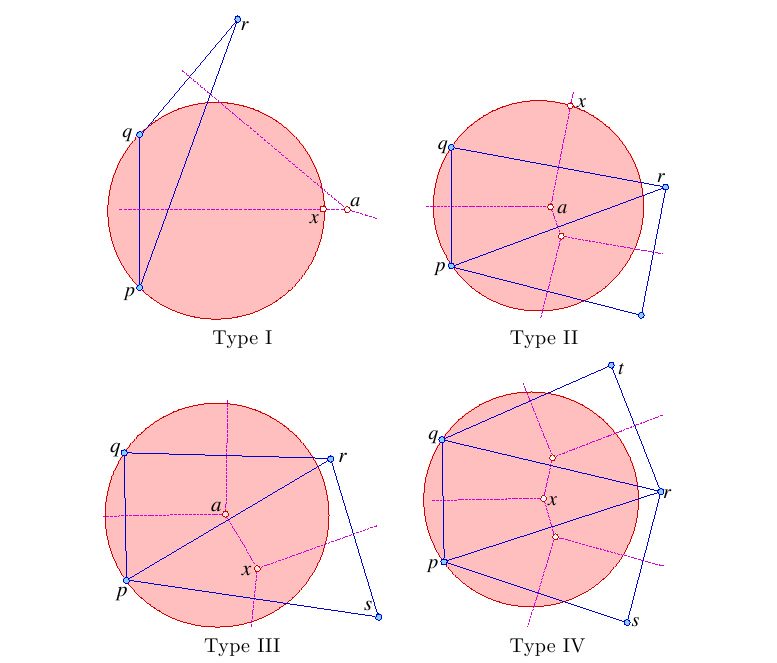
Find a point x inside the (shaded disk) petal of pq that is furthest away from all existing
vertices. Such a point can be on a Voronoi edge (top) or a Voronoi vertex (bottom). Type I: on the
dual of pq. Type II: on a Voronoi edge other than the dual of pq. Type III: a circumcenter other
than that of pqr. Type IV: the circumcenter of pqr.
Note that our approach nicely unifies the previously known Steiner point insertion techniques: circumcenter (Type V) of Chew and Ruppert, off-center (Type I) of Ungor, and sink (Type III) of Edelsbrunner and Guoy
together with a new one (Type II).
Unlike the previous Delaunay refinement methods, we use circumcenters less frequently. This allows us to reach better minimum angle quality.
Algorithm
Compute the Delaunay triangulation of the input
while there exists a bad triangle pqr with shortest edge pq
insert a point x is in petal(pq) of its shortest edge pq
that is furthest from all existing vertices |
Refinement and Relocation
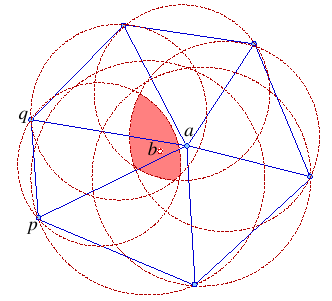
Relocating a free vertex of a bad triangle pqr to the intersection of the petals of the link
of a = r.
Algorithm
Compute the Delaunay triangulation (DelTri) of the input
Let P denote the maintained point set
while there exists a bad triangle pqr in DelTri(P) with shortest edge pq
relocated := False
for each free vertex a of pqr
if K = intersection of petal(xy), where xy is in link(a), is not empty set
and there exists a b in K such that all triangles of star(b) in the DelTri(P+{b}-{a}) are good
then
delete a; insert b; relocated:=True; break;
endfor
if relocated == False then
insert a point x is in petal(pq) of the bad triangle's shortest edge pq
that is furthest from all existing vertices
endwhile
|
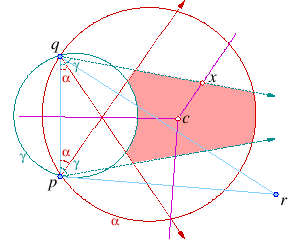
Triangulations without Small and Large Angles
Feasible region slice is the intersection of [alpha, gamma]-crescent, alpha-
wedge, and gamma-slab. A point x inside this region that is furthest away from
all existing vertices is chosen as a refinement point (left). A bad triangle pqa is fixed by relocating one of its vertices a
into b which is a point in the intersection (shaded) of the [alpha, gamma]-slices of
the edges on the link of a (right).
Algorithm
Compute the Delaunay triangulation (DelTri) of the input
Let P denote the maintained point set
while there exists a bad triangle pqr in DelTri(P) with shortest edge pq
relocated := False
for each free vertex a of pqr
forevery edge xy on the link of a
Compute alpha-wedge(xy)
Compute gamma-slab(xy)
Compute [alpha, gamma]-crescent(xy)
Compute [alpha, gamma]-slice(xy)
endfor
if K = intersection of [alpha, gamma]-slice(xy), where xy is in link(a), is not empty set
and there exists a b in K such that all triangles of star(b) in the DelTri(P+{b}-{a}) are good
then
delete a; insert b; relocated:=True; break;
endfor
if relocated == False then
insert a point x is in [alpha, gamma]-slice(xy) of the bad triangle's shortest edge pq
that is furthest from all existing vertices
endwhile
|