aCute A premium quality meshing software.

Implemented and licensed at the University of Florida, Gainesville
Partially funded by an NSF CAREER Award and an NSF Regular Grant
Contact: Alper Ungor, CISE Department, University of Florida, Gainesville, FL, 32611 ungoratcisedotufldotedu

• Overview
• Quality
• Algorithm
• Output Size
• Download
• References

Quality Comparison

Here, we demonstrate some features of aCute in generating premium quality triangulations. First, the termination problem is illustrated, where the previous Delaunay refinement algorithms result in an infinite loop when the constraint minimum angle around 34 degrees. Then, sample output quality triangulations generated by aCute are given. Next, sample output triangulations generated by aCute with no small no large angles are shown, where aCute combines minimum and maximum angle constraints at the same time. Also, our results on uniform triangulations are shown, where we use minimum triangle area as the additional constraint to generate uniform quality triangulations.

Termination Problem

Shewchuks experimental study revealed that the Delaunay refinement algorithm in practice works better than its theoretical guarantee [She96]:

Ruppert [Rup93] proves that this procedure halts for angle constraint of up to 20.7 degrees. In practice, the algorithm generally halts with an angle constraint of 33.8 degrees, but often fails to terminate given an angle constraint of 33.9 degrees. It would be interesting to discover why the cut-off falls there.

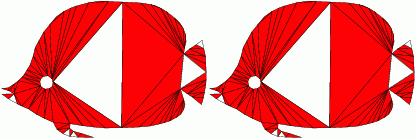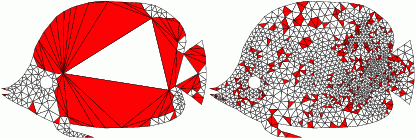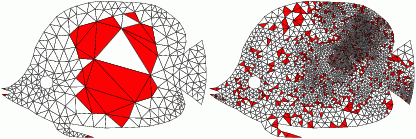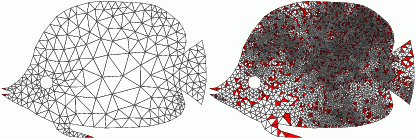
The iterative refinement process could introduce smaller and smaller features and may not terminate which is referred to the termination problem. This behavior can be shown as follows:

                                    

Minimum Angle Quality

aCute	Triangle
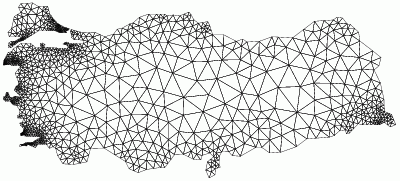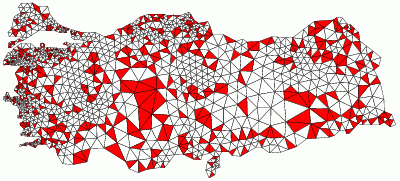Smallest angle: 41 degrees	Smallest angle: 33 degrees Does not terminate for smallest angle > 34.1 degrees
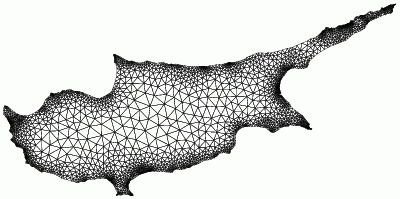Smallest angle: 41 degrees	Smallest angle: 32 degrees Does not terminate for smallest angle > 33.9 degrees
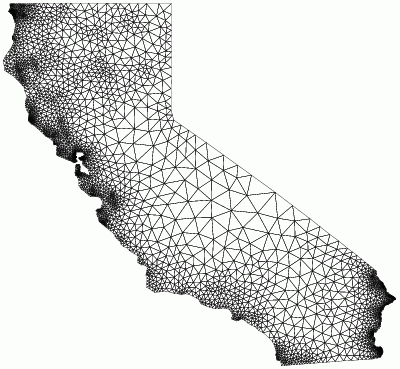Smallest angle: 42 degrees	Smallest angle: 33 degrees Does not terminate for smallest angle > 34 degrees

Minimum Angle and Maximum Angle Quality

aCute	Triangle
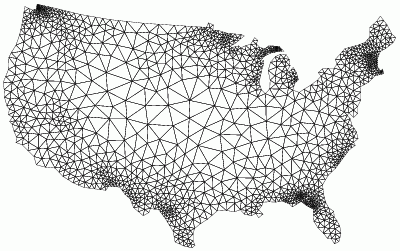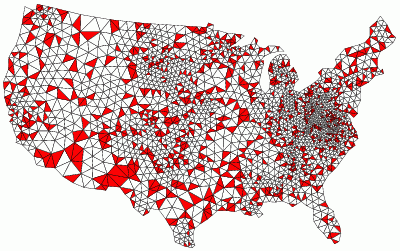Smallest angle: 35 degrees Largest angle: 85 degrees	Smallest angle: 34.012 degrees Largest angle: 111.68 degrees
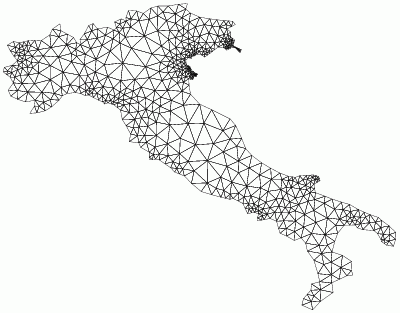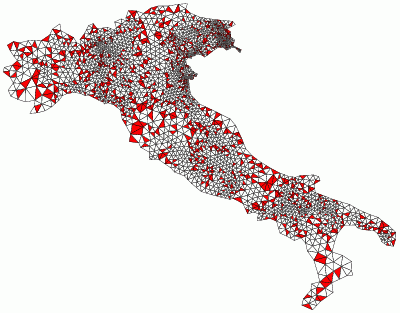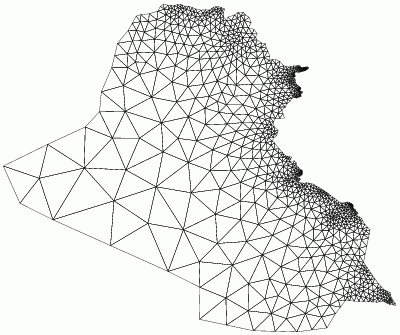
Smallest angle: 40 degrees Largest angle: 88 degrees	Smallest angle: 34.01 degrees Largest angle: 111.98 degrees
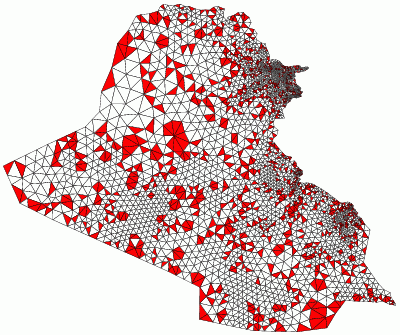Smallest angle: 40 degrees Largest angle: 88 degrees	Smallest angle: 34.003 degrees Largest angle: 111.95 degrees

Premium Quality Uniform Triangulations

aCute	Triangle
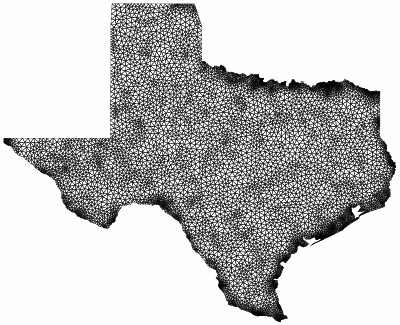
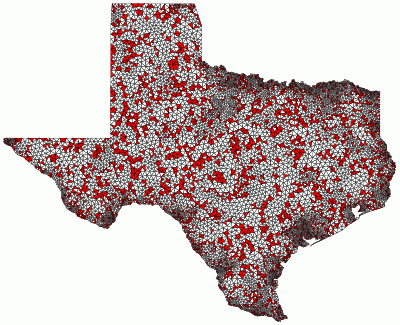
Smallest angle: 41.5 degrees Minimum area = 150 Shortest edge = 1	Smallest angle: 33 degrees Minimum area = 150 Shortest edge = 1
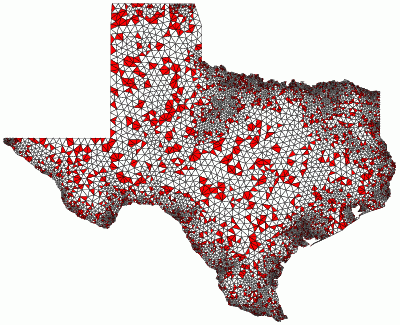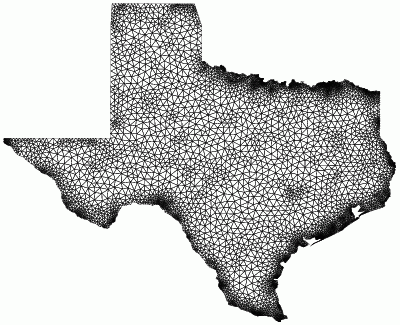
Smallest angle: 41.5 degrees Minimum area = 325 Shortest edge = 1	Smallest angle: 33 degrees Minimum area = 325 Shortest edge = 1
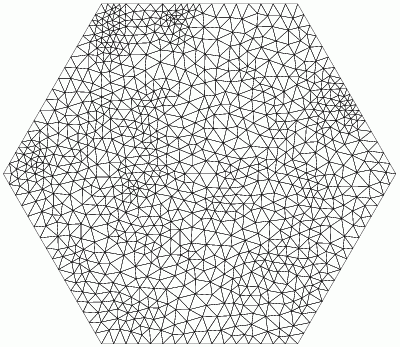
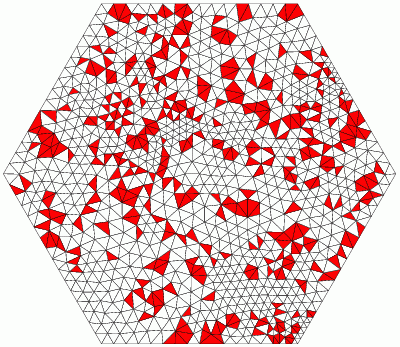
Smallest angle: 38 degrees, Largest angle: 88 degrees Minimum area = 0.003, Shortest edge = 0.0036674	Smallest angle: 32.017 degrees, Largest angle: 115.36 degrees Minimum area = 0.003, Shortest edge = 0.0036674
Smallest angle: 40 degrees, Largest angle: 86 degrees Minimum area = 0.05, Shortest edge = 0.3	Smallest angle: 34 degrees, Largest angle: 111.87 degrees Minimum area = 0.05, Shortest edge = 0.3

• Overview
• Quality
• Algorithm
• Output Size
• Download
• References