In this project, we developed a framework for constructing nested Riemannian homogeneous spaces. Intuitively a Riemannian manifold is a homogeneous space if all points on it look locally alike. Examples of such spaces include but are not limited to, the n-dimensional space of reals, n-sphere, Grassmanian, Stiefel manifold, hyperbolic space, manifold of SPD matrices etc. Homogeneous spaces are encountered in numerous applications of Engineering and Science. Dimensionality reduction in such spaces is essential when dealing with high-dimensional data sets. Principal Geodesic Analysis (PGA), the nonlinear counter part of traditional principal component analysis (PCA) is applicable to such data but has the drawback that the lower dimensional manifolds produced are geodesic sub-manifolds and are required to pass through the (Frechet) mean of the data. A nested spaces (sub-manifolds) does not have this requirement and hence can capture data trends that are much more general. We present a general recipe for construction of such nested homogeneous spaces and present examples of nested Grassman manifolds and nested hyperbolic spaces. In the latter case, we show how the nested hypserbolic spaces can be used as a building block in developing graph convolutional neural networks (GCN) which we call nested hyperbolic graph convolutional neural networks (NHGCN). Performance of the dimensionality reduction and pattern classification algorithms are showcased via several synthetic and real data experiments in the three related papers listed here. Webpage.
 

[Chun-Hao Yang and Baba C. Vemuri Intl. Conf. on Information Processing in Medical Imaging (IPMI) 2021 journal of Machine Learning in Biomedical Image Analysis (MELBA) 2022 Xiran Fan, Chun-Hao Yang and Baba C. Vemuri IEEE Computer Vision and Pattern Recognition (CVPR) 2022 ]

In this project, we address the problem of video tracking using covariance descriptors constructed from simple features extracted from the given image sequence. Theoretically, this can be posed as a tracking problem in the space of (n,n) symmetric positive definite (SPD) matrices denoted by $P_n$. A novel probabilistic dynamic model in $P_n$ based on Riemannian geometry and probability theory is presented in conjunction with a geometric (intrinsic) recursive filter for tracking a time sequence of SPD matrix measurements in a Bayesian framework. This newly developed filtering method can be used for the covariance descriptor updating problem in covariance tracking, leading to new and efficient video tracking algorithms. In the accomapnying paper (SIAM journal of Imaging Science 2013), we demonstrate the accuracy and efficiency of our tracker in comparison to the state-of-the-art via synthetic experiments on $P_n$, and several real data experiments for tracking in video sequences. Further details can be found in our paper in SIAM Journal of Imaging Science 2013. Webpage.
 

[Guang Cheng and Baba C Vemuri SIAM J. Imag. Sci. (SIMS) 2013]

In this project, we developed novel algorithms to compute robust statistics from manifold-valued data. Specifically, we developed algorithms for estimating the robust Frechet Mean (FM) and performing a robust exact-principal geodesic analysis (ePGA) for data lying on known Riemannian manifolds. We formulate the minimization problems involved in both these problems using the minimum distance estimator called the L$_2$E. This leads to a nonlinear optimization which is solved efficiently using a Riemannian accelerated gradient descent technique. We show competitive performance results of our algorithms applied to synthetic data with outliers, the corpus callosum shapes extracted from OASIS MRI database, and diffusion MRI scans from movement disorder patients respectively. Further details on various applications of this work appear in our paper in the Intl. Conf. on Info. Processing in Med. Img. (IPMI) 2017. Webpage.
 

[Monami Banerjee and Baba C Vemuri Info. Processing in Med. Img. (IPMI) 2017]

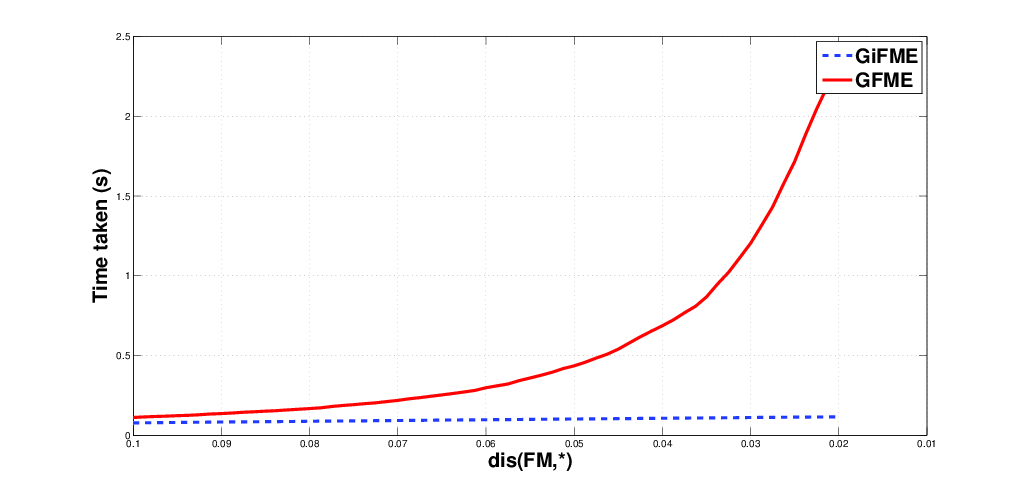
In this project, we developed a recursive Frechet mean (FM) estimator for data points residing on a Grassman manifold. Grassman manifold is a Riemannian manifold where each point on it is a linear subspace of n-dimensional Euclidean space. We prove the weak consistency of our FM estimator and compare our estimator performance with respect to the standard gradient descent based FM computation algorithm. Our FM estimator has the advantage that it is well suited for streaming data applications i.e., where data are incrementally acquired. Thus, it is an online FM estimator. We perform Principal geodesic analysis ofthe given data on the Grassmanian and use it in cunjuntion with a nearrest-neighbor classifier to perform action recognition from videos. In the accompanying figure here, we depict the performance of our FM estimator (GiFME) against the gradient descent based FM estimator (GFME) and as evident, the time taken to estimate as a function of input number of sample data points on the Grassmanian (for synthetic data) is much smaller for GiFME in comparison to GFME. Further details on various applications of this work appear in our IEEE ICCV 2015 paper. Webpage.
 

[Rudrasis Chakraborty and Baba C Vemuri IEEE ICCV 2015]

[Kumar et al. IPMI 09] [Barmpoutis et al IPMI 09] [Barmpoutis et al. NeuroImage 09]
[Kumar et al. MMBIA 08] [Barmpoutis et al. MICCAI 08] [Barmpoutis et al. ISBI 08]
 [Jian et al. IPMI 07] [Jian et al. NeuroImage 07]

We propose a new concept class based on conic sections that is suited for high dimensional sparse data. Each class is assigned a conic section in the input space, described by its focus (point), directrix (hyperplane) and eccentricity (value). Class labels are assigned to data-points based on the eccentricities attributed to them by the class descriptors. The concept class can represent non-linear discriminant boundaries with merely four times the number of parameters as a linear discriminant. Learning involves updating the class descriptors. We also present a tractable learning algorithm for binary classification. For each descriptor, we track its feasible space that results in identical labeling for classified points. We then pick a solution from it to learn misclassified points as well as pursue simpler (near-linear) boundaries. The performance of our classifier is comparable to state-of-the-art and out-performed them on several data sets. Webpage.

[Kodipaka et al. CVPR 08] [Banerjee et al. CVPR 06]

The hypothesis being that the shape asymmetry between the left and the right hippocampus can indicate the hemispheric location of an epileptic focus. The scans of two classes of patients with epilepsy, those with a right and those with a left medial temporal lobe focus (RATL and LATL), as validated by clinical consensus and subsequent surgery, were compared to a set of age and sex matched healthy volunteers using both volume and shape based features. Shape-based features are derived from the displacement field characterizing the non-rigid deformation between the left and right hippocampi of a control or a patient as the case may be. Using the shape-based features, the results show a significant improvement in distinguishing between the controls and the rest (RATL and LATL) vis-a-vis volume-based features. Using a novel feature, namely, the normalized histogram of the 3D displacement field, we also achieved significant improvement over the volume-based feature in classifying the patients as belonging to either of the two classes LATL or RATL respectively. It should be noted that automated identification of hemispherical foci of epilepsy has not been previously reported.

[Lord et al. TMI 07][Lord et al. SSVM 07][Lord et al. ICCV 07]
[Kodipaka et al. MedIA 07]

We present continuous mixture models which are spatially varying, adaptive, convolution based approaches for smoothing and segmentation. These new and innovative approaches afford to preserve the complicated local geometries of the boundaries of objects in real scenes without using any prior information. First, we extract the local orientation information using Gabor filters. The orientation information at each lattice point is then represented by a continuous mixture of oriented Gaussians. The continuous mixture representation is cast as the Laplace transform of the mixing density over the space of covariance (positive definite) matrices. This mixing density is assumed to be in a parameterized form, namely, a mixture of Wisharts, whose Laplace transform evaluates to a closed form expression called the Rigaut type function: a scalar-valued function of the parameters of the Wishart distribution. The weights in the mixture are then computed using a sparse deconvolution technique. In the second stage, we construct the convolution kernels for smoothing/segmentation using these weights within the continuous mixture kernel.

[Subakan et al. CVPR 08] [Subakan et al. ICCV 07]