Finding Realizations of Isostatic Barjoint Frameworks of Corner Sharing Triangles: The CayMos Approach

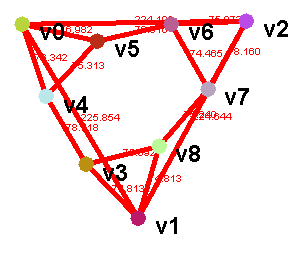
The picture to the right is the type of corner sharing triangle isostatic bar-joint structures we are interested in. The tri-hex is the smallest interesting case of these. In the picture to the right, the triangle v0-v1-v2 is the "outer" boundary triangle and the hexagon v3-v4-v5-v6-v7-v8 is the "inner" hexagon. The three other triangles are the triangles that make up the vertex-adjacent triangle graphs.

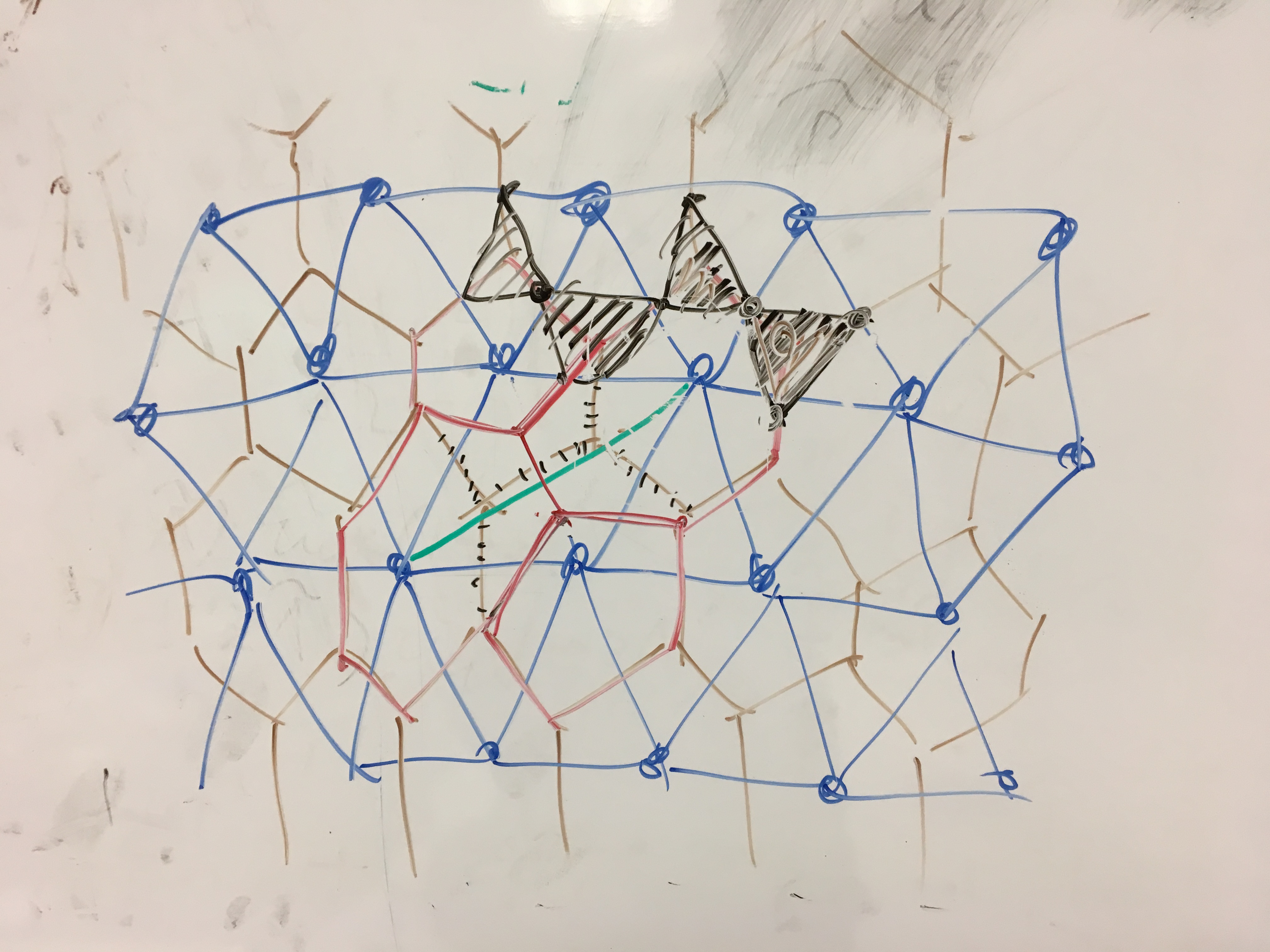
The above picture shows how to construct corner sharing equilateral triangle graphs and the process by which all such graphs can be constructed. Notice that four 6-cycles have become two 5-cycles and two 7-cycles through an edge exchange.

We have used the CayMos software to create and analyze the tri-hex graph. The source code should be downloaded here instead of the previous link and should be built using Eclipse.

There are four relevant papers for understanding the CayMos approach: 1, 2, 3, 4

The idea of the CayMos approach is to first drop an edge, (in our example case, the dropped edge is v2v3). As the resulting "low cayley complexity" 1-degree of freedom linkage moves (driving cayley parameter being v1v7), we can simply measure the distance between v2 and v3 to find the realizations that attain the given distance between v2 and v3.

The CayMos approach works for arbitrarily large cornersharing triangle (CoST) cases especially if they are permitted to have substructures that are isostatic. Even otherwise, it works for at least one family of arbitrarily large CoST's, but for full generality another method is being implemented (Optimal Modification for Decomposition or OMD).

The upper bound on the number of solutions of trihex computed by the CayMos theory is 128. There are known to be nearly 100 solutions in one case, so the upper bound is pretty good.

The Videos

Clicking the links to the left takes you to videos of the configurations of the trihex graph for various ratios of the edge lengths of the outer triangle to those of the inner hexagon.

The curve shown in 3D is a bijection from a connected component of the configuration space and has been proven to be homeomorphic to a circle (assuming no pairs of lengths are equal and triangle orientations are fixed - this is because the 3 colored dotted edges make the graph globally rigid when the triangle orientations are fixed).

Any intersections are illusions because the 3D curve is projected onto 2D. Cusps can be resolved if necessary, but we didn't do it.

The colored portions of the curve represent the relative orientations of triples of vertices that don't form triangles (there are 3 such triples and hence 8 such orientations).

Once the relative orientations of the triangles are considered as well, we could have more connected components. Furthermore, each connected component can provide multiple realizations that attain the dropped length for each relative orientation of the triangles containing v2 and v3

The upper bound on the number of solutions of trihex computed by the CayMos theory is 128. There are known to be nearly 100 solutions in one case, so the upper bound is pretty good.