Matrix properties
number of rows	7,224
number of columns	7,224
nonzeros	54,082
structural full rank?	yes
structural rank	7,224
# of blocks from dmperm	1,204
# strongly connected comp.	1,204
explicit zero entries	0
nonzero pattern symmetry	15%
numeric value symmetry	0%
type	real
structure	unsymmetric
Cholesky candidate?	no
positive definite?	no

author	G. Geng
editor	T. Davis
date	2009
kind	power network problem
2D/3D problem?	no

Additional fields	size and type
b	sparse 7224-by-5

Notes:

Transient stability-constrained optimal power flow (TSOPF) problems from     
Guangchao Geng, Institute of Power System, College of Electrical Engineering,
Zhejiang University, Hangzhou, 310027, China.  (genggc AT gmail DOT com).    
Matrices in the  Full-Space (FS) group are symmetric indefinite, and are best
solved with MA57.  Matrices in the the Reduced-Space (RS) group are best     
solved with KLU, which for these matrices can be 10 times faster than UMFPACK
or SuperLU.                                                                  

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	80,388
Cholesky flop count	9.0e+05
nnz(L+U), no partial pivoting, with AMD	153,552
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	15,765
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	86,525

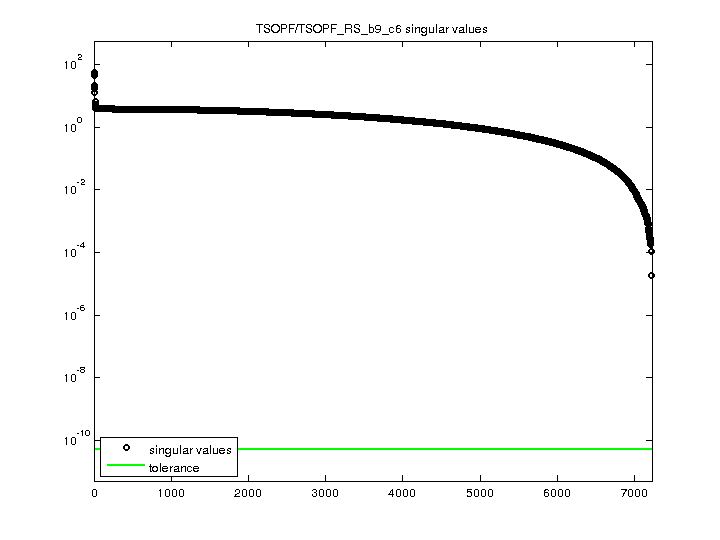
SVD-based statistics:
norm(A)	55.4816
min(svd(A))	1.79163e-05
cond(A)	3.09671e+06
rank(A)	7,224
sprank(A)-rank(A)	0
null space dimension	0
full numerical rank?	yes

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.