Matrix properties
number of rows	2,454
number of columns	2,454
nonzeros	25,032
structural full rank?	yes
structural rank	2,454
# of blocks from dmperm	2
# strongly connected comp.	2
explicit zero entries	0
nonzero pattern symmetry	symmetric
numeric value symmetry	symmetric
type	real
structure	symmetric
Cholesky candidate?	no
positive definite?	no

author	G. Geng
editor	T. Davis
date	2009
kind	power network problem
2D/3D problem?	no

Additional fields	size and type
b	sparse 2454-by-1

Notes:

Transient stability-constrained optimal power flow (TSOPF) problems from     
Guangchao Geng, Institute of Power System, College of Electrical Engineering,
Zhejiang University, Hangzhou, 310027, China.  (genggc AT gmail DOT com).    
Matrices in the  Full-Space (FS) group are symmetric indefinite, and are best
solved with MA57.  Matrices in the the Reduced-Space (RS) group are best     
solved with KLU, which for these matrices can be 10 times faster than UMFPACK
or SuperLU.                                                                  

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	33,878
Cholesky flop count	5.8e+05
nnz(L+U), no partial pivoting, with AMD	65,302
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	524,463
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	884,993

SVD-based statistics:
norm(A)	5306.19
min(svd(A))	7.34197e-09
cond(A)	7.22721e+11
rank(A)	2,454
sprank(A)-rank(A)	0
null space dimension	0
full numerical rank?	yes

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

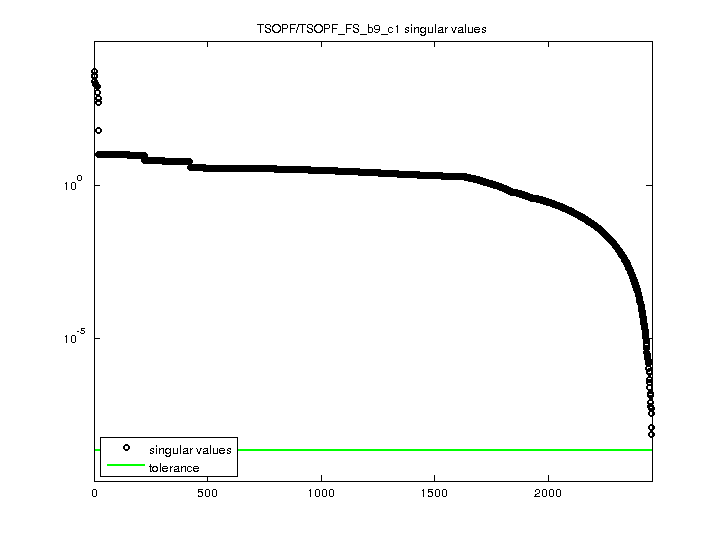
For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.