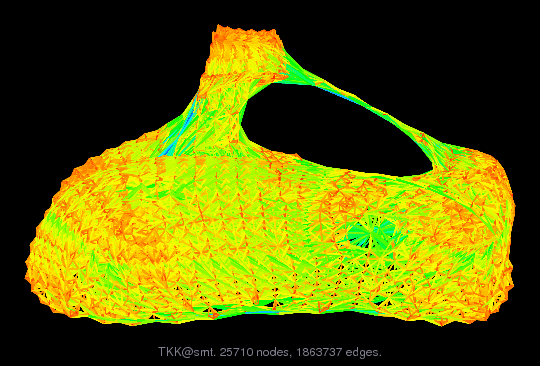
Matrix: TKK/smt
Description: 3D model, thermal stress analysis of surface mounted transistor. R Kohia
 |
| (undirected graph drawing) |
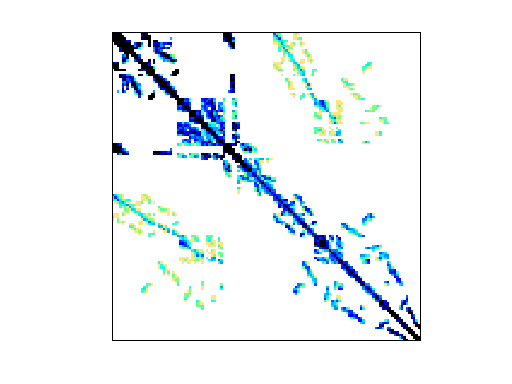 |
 |
| Matrix properties | |
| number of rows | 25,710 |
| number of columns | 25,710 |
| nonzeros | 3,749,582 |
| structural full rank? | yes |
| structural rank | 25,710 |
| # of blocks from dmperm | 1 |
| # strongly connected comp. | 1 |
| explicit zero entries | 3,602 |
| nonzero pattern symmetry | symmetric |
| numeric value symmetry | symmetric |
| type | real |
| structure | symmetric |
| Cholesky candidate? | yes |
| positive definite? | yes |
| author | R. Kouhia |
| editor | T. Davis |
| date | 2008 |
| kind | structural problem |
| 2D/3D problem? | yes |
| Additional fields | size and type |
| b | full 25710-by-1 |
| coord | full 25710-by-3 |
Notes:
Matrix problems from Reijo Kouhia, Structural Mechanics, Helsinki
University of Technology. http://users.tkk.fi/~kouhia/sparse.html
Surface mount transistor, 1704 reduced triquadratic elem, therm stress.
This is a stiffness matrix from a thermal stress analysis of
a surface mounted transistor. Due to symmetry only one half of
the model is discretized in 1704 standard reduced triquadratic elements
(20 node serendipity). There are 5 different materials.
The stiffness matrix is integrated by 3x3x3 Gaussian quadrature.
Separate load vector file is also available.
Figure of the FE model can be seen in a separate description,
or downloaded as a postscript file from the contributors www-pages.
Contributor:
Reijo Kouhia, Helsinki University of Technology,
Laboratory of Structural Mechanics
PO Box 2100, 02015 HUT, Finland
e-mail: reijo.kouhia@hut.fi
http://www.hut.fi/~kouhia
| Ordering statistics: | result |
| nnz(chol(P*(A+A'+s*I)*P')) with AMD | 14,601,688 |
| Cholesky flop count | 1.4e+10 |
| nnz(L+U), no partial pivoting, with AMD | 29,177,666 |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 26,940,204 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 65,904,871 |
Note that all matrix statistics (except nonzero pattern symmetry) exclude the 3602 explicit zero entries.
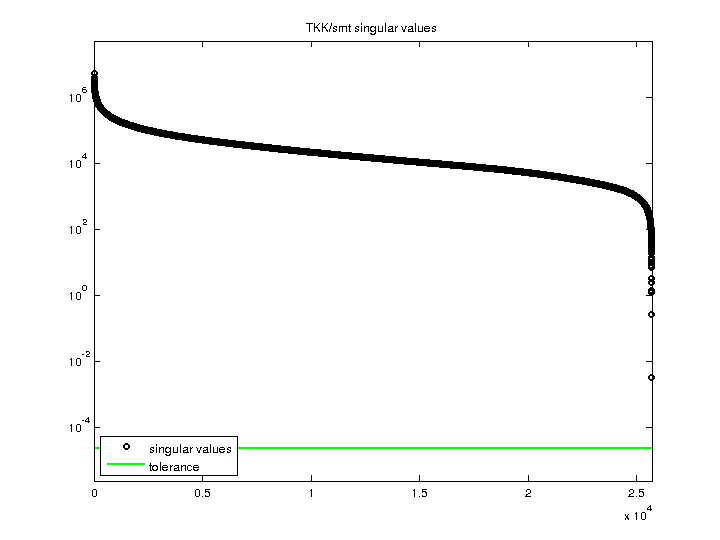
| SVD-based statistics: | |
| norm(A) | 5.29766e+06 |
| min(svd(A)) | 0.00333867 |
| cond(A) | 1.58676e+09 |
| rank(A) | 25,710 |
| sprank(A)-rank(A) | 0 |
| null space dimension | 0 |
| full numerical rank? | yes |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (A)) |
| status: | ok |
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.