
Matrix: Rommes/S10PI_n
Description: Transmission line, 10 sections, SISO, index-2 DAE (CEPEL, Brazil)
 |
| (undirected graph drawing) |
 |
 |
| Matrix properties | |
| number of rows | 682 |
| number of columns | 682 |
| nonzeros | 1,633 |
| structural full rank? | no |
| structural rank | 679 |
| # of blocks from dmperm | 96 |
| # strongly connected comp. | 1 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | symmetric |
| numeric value symmetry | 11% |
| type | real |
| structure | unsymmetric |
| Cholesky candidate? | no |
| positive definite? | no |
| author | F. Freitas |
| editor | J. Rommes |
| date | 2010 |
| kind | eigenvalue/model reduction problem |
| 2D/3D problem? | yes |
| Additional fields | size and type |
| B | sparse 682-by-1 |
| C | sparse 1-by-682 |
| E | sparse 682-by-682 |
Notes:
Power system models from Joost Rommes, Nelson Martins, Francisco Freitas
This collection of power system models originates from real power systems,
mostly based on Brazilian interconection power systems (BIPS) models (the file
names refer to the actual power system related to a given year electric load
scenario). These systems [E dx/dt = Ax + Bu ; y=Cx + Du] are interesting
benchmarks for several numerical algorithms, including eigenvalue algorithms
(dominant modes/poles/zeros, stability analysis, computing rightmost
eigenvalues and/or with smallest damping ratio, eigenvalue parameter
sensitivity) and model order reduction (large-scale DAEs ). Refer to the
corresponding publications for more details on the systems and numerical
results of several eigenvalue/model order reduction algorithms. For
corresponding software, see http://sites.google.com/site/rommes/software
If E is not present in the problem, then E=I should be assumed.
If D is not present, D=0 should be assumed. (Note that as of Jan 2011,
no problem has a nonzero D).
The iv vector in some of the files is a vector with nonzeros (ones) at indices
that represent state-variables (the zeros are algebraic variables). One can
construct the descriptor matrix E by E=spdiags(iv,0,n,n). This iv vector is
generated by the Brazilian power system simulation software, and can be more
efficient to compute with.
Test systems:
All power system models originate from CEPEL ( http://www.cepel.br/ )
power system file n #inputs #outputs references
------------ ---- ------ ------- -------- --
New England ww_36_pmec_36 66 1 1 [1]
BIPS/97 ww_vref_6405 13251 1 1 [1]
BIPS/2007 xingo_afonso_itaipu 13250 1 1 [2]
BIPS/97 mimo8x8_system 13309 8 8 [3]
BIPS/97 mimo28x28_system 13251 28 28 [3]
BIPS/97 mimo46x46_system 13250 46 46 [4]
Juba5723 juba40k 40337 2 1 [5]
Bauru5727 bauru5727 40366 2 2 [5]
zeros_nopss zeros_nopss_13k 13296 46 46 [5]
xingo6u descriptor_xingo6u 20738 1 6 [5]
nopss nopss_11k 11685 1 1 [5]
xingo3012 xingo3012 20944 2 2 [5]
bips98_606 bips98_606 7135 4 4 [6]
bips98_1142 bips98_1142 9735 4 4 [6]
bips98_1450 bips98_1450 11305 4 4 [6]
bips07_1693 bips07_1693 13275 4 4 [6]
bips07_1998 bips07_1998 15066 4 4 [6]
bips07_2476 bips07_2476 16861 4 4 [6]
bips07_3078 bips07_3078 21128 4 4 [6]
Several SISO/MIMO test systems, whose main components are transmission lines
(TL) are available. TLs are modeled by ladder networks, comprised of cascaded
RLC PI-circuits, having fixed parameters.
Transmission lines with 10--80 PI Sections are considered.
PIsections10to80.zip [Submitted]
There are two kinds of files for representing a same system: the file with
termination _n refers to an index-2 system DAE model, while _n1 means
a model of the same system, but for an index-1 DAE representation. The
representation of each test system has the form [E dx/dt = Ax + Bu ; y=Cx]
References:
[1] ROMMES, J., MARTINS, N., Efficient computation of transfer function
dominant poles using subspace acceleration. IEEE Trans. on Power Systems,
Vol. 21, Issue 3, Aug. 2006, pp. 1218-1226
[2] ROMMES, J., MARTINS, N., Computing large-scale system eigenvalues most
sensitive to parameter changes, with applications to power system
small-signal stability , IEEE Transactions on Power Systems, Vol. 23, Issue
2, May 2008, pp. 434-442
[3] ROMMES, J., MARTINS, N., Efficient computation of multivariable transfer
function dominant poles using subspace acceleration. 2006, IEEE Trans. on,
Power Systems, Vol. 21, Issue 4, Nov. 2006, pp. 1471-1483.
[4] MARTINS, N., PELLANDA, P.C.,ROMMES, J., Computation of transfer function
dominant zeros with applications to oscillation damping control of large
power systems, IEEE Trans. on Power Systems, Vol. 22, Issue 4, Nov. 2007,
pp. 1657-1664
[5] ROMMES, J., MARTINS, N., FREITAS, F., Computing Rightmost Eigenvalues for
Small-Signal Stability Assessment of Large-Scale Power Systems, IEEE
Transactions on Power Systems, Vol. 25, Issue 2, May 2010, pp.929-938
[6] FREITAS, F., ROMMES, J., MARTINS, N., Gramian-Based Reduction Method
Applied to Large Sparse Power System Descriptor Models, IEEE Transactions
on Power Systems, Vol. 23, Issue 3, August 2008, pp. 1258-1270
| Ordering statistics: | result |
| nnz(chol(P*(A+A'+s*I)*P')) with AMD | 1,849 |
| Cholesky flop count | 5.2e+03 |
| nnz(L+U), no partial pivoting, with AMD | 3,016 |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 1,802 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 2,937 |
| SVD-based statistics: | |
| norm(A) | 66.8081 |
| min(svd(A)) | 1.65915e-16 |
| cond(A) | 4.02665e+17 |
| rank(A) | 679 |
| sprank(A)-rank(A) | 0 |
| null space dimension | 3 |
| full numerical rank? | no |
| singular value gap | 7.59205e+09 |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (A)) ; |
| status: | ok |
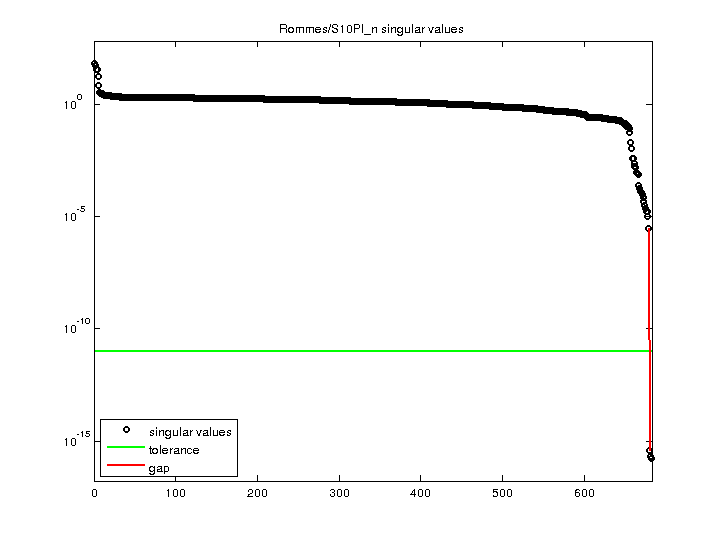
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.