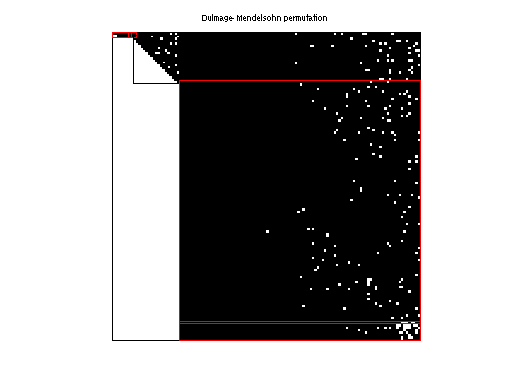
Matrix properties
number of rows	24,430
number of columns	24,421
nonzeros	299,756
structural full rank?	no
structural rank	22,981
# of blocks from dmperm	3,671
# strongly connected comp.	1,231
explicit zero entries	0
nonzero pattern symmetry	0%
numeric value symmetry	0%
type	binary
structure	rectangular
Cholesky candidate?	no
positive definite?	no

author	D. Priebel
editor	T. Davis
date	2009
kind	combinatorial problem
2D/3D problem?	no

Additional fields	size and type
factor_base	full 24421-by-1
smooth_number	full 24430-by-32
solution	full 8741-by-1

Notes:

Each column in the matrix corresponds to a number in the factor base          
less than some bound B.  Each row corresponds to a smooth number (able        
to be completely factored over the factor base).  Each value in a row         
binary vector corresponds to the exponent of the factor base mod 2.           
For example:                                                                  
                                                                              
    factor base: 2 7 23                                                       
    smooth numbers: 46, 28, 322                                               
    2^1       * 23^1 = 46                                                     
    2^2 * 7^1        = 28                                                     
    2^1 * 7^1 * 23^1 = 322                                                    
    Matrix:                                                                   
        101                                                                   
        010                                                                   
        111                                                                   
                                                                              
A solution to the matrix is considered to be a set of rows which when         
combined in GF2 produce a null vector. Thus, if you multiply each of          
the smooth numbers which correspond to that particular set of rows you        
will get a number with only even exponents, making it a perfect               
square. In the above example you can see that combining the 3 vectors         
results in a null vector and, indeed, it is a perfect square: 644^2.          
                                                                              
Problem.A: A GF(2) matrix constructed from the exponents of the               
factorization of the smooth numbers over the factor base. A solution of       
this matrix is a kernel (nullspace). Such a solution has a 1/2 chance of      
being a factorization of N.                                                   
                                                                              
Problem.aux.factor_base: The factor base used. factor_base(j) corresponds     
to column j of the matrix. Note that a given column may or may not have       
nonzero elements in the matrix.                                               
                                                                              
Problem.aux.smooth_number: The smooth numbers, smooth over the factor         
base.  smooth_number(i) corresponds to row i of the matrix.                   
                                                                              
Problem.aux.solution: A sample solution to the matrix. Combine, in GF(2)      
the rows with these indicies to produce a solution to the matrix with the     
additional property that it factors N (a matrix solution only has 1/2         
probability of factoring N).                                                  
                                                                              
Problem specific information:                                                 
                                                                              
n = 239380926372595066574100671394554319947805305453767699448870971 (208-bits)
passes primality test, n is composite, continuing...                          
1) Initial bound: 650000, pi(650000) estimate: 48562,                         
    largest found: 592903 (actual bound)                                      
2) Number of quadratic residues estimate: 32376, actual number found: 24420   
3) Modular square roots found: 48840(2x residues)                             
4) Constructing smooth number list [sieving] (can take a while)...            
Sieving for: 24430                                                            
5. Constructing a matrix of size: 24430x24421                                 
Set a total of 299756 exponents, with 12070 negatives                         
Matrix solution found with: 8741 combinations                                 
Divisor: 12216681953629826483019726942851 (probably prime)                    
Divisor: 19594594283554225566102143686121 (probably prime)                    

Ordering statistics:	result
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	63,577,458
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	53,620,282

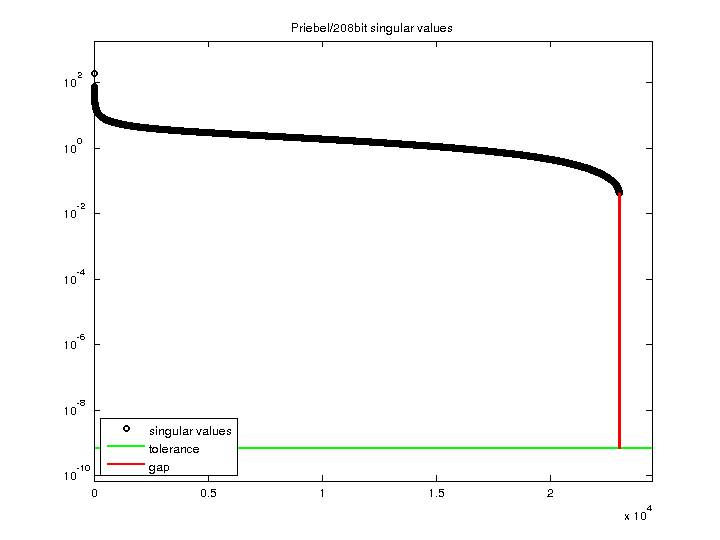
SVD-based statistics:
norm(A)	190.896
min(svd(A))	0
cond(A)	Inf
rank(A)	22,981
sprank(A)-rank(A)	0
null space dimension	1,440
full numerical rank?	no
singular value gap	Inf

singular values (MAT file):	click here
SVD method used:	s = svd (full (R)) ; where [~,R,E] = spqr (A) with droptol of zero
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.