Matrix properties
number of rows	3,606
number of columns	3,597
nonzeros	37,118
structural full rank?	no
structural rank	3,460
# of blocks from dmperm	376
# strongly connected comp.	122
explicit zero entries	0
nonzero pattern symmetry	0%
numeric value symmetry	0%
type	binary
structure	rectangular
Cholesky candidate?	no
positive definite?	no

author	D. Priebel
editor	T. Davis
date	2009
kind	combinatorial problem
2D/3D problem?	no

Additional fields	size and type
factor_base	full 3597-by-1
smooth_number	full 3606-by-25
solution	full 1474-by-1

Notes:

Each column in the matrix corresponds to a number in the factor base     
less than some bound B.  Each row corresponds to a smooth number (able   
to be completely factored over the factor base).  Each value in a row    
binary vector corresponds to the exponent of the factor base mod 2.      
For example:                                                             
                                                                         
    factor base: 2 7 23                                                  
    smooth numbers: 46, 28, 322                                          
    2^1       * 23^1 = 46                                                
    2^2 * 7^1        = 28                                                
    2^1 * 7^1 * 23^1 = 322                                               
    Matrix:                                                              
        101                                                              
        010                                                              
        111                                                              
                                                                         
A solution to the matrix is considered to be a set of rows which when    
combined in GF2 produce a null vector. Thus, if you multiply each of     
the smooth numbers which correspond to that particular set of rows you   
will get a number with only even exponents, making it a perfect          
square. In the above example you can see that combining the 3 vectors    
results in a null vector and, indeed, it is a perfect square: 644^2.     
                                                                         
Problem.A: A GF(2) matrix constructed from the exponents of the          
factorization of the smooth numbers over the factor base. A solution of  
this matrix is a kernel (nullspace). Such a solution has a 1/2 chance of 
being a factorization of N.                                              
                                                                         
Problem.aux.factor_base: The factor base used. factor_base(j) corresponds
to column j of the matrix. Note that a given column may or may not have  
nonzero elements in the matrix.                                          
                                                                         
Problem.aux.smooth_number: The smooth numbers, smooth over the factor    
base.  smooth_number(i) corresponds to row i of the matrix.              
                                                                         
Problem.aux.solution: A sample solution to the matrix. Combine, in GF(2) 
the rows with these indicies to produce a solution to the matrix with the
additional property that it factors N (a matrix solution only has 1/2    
probability of factoring N).                                             
                                                                         
Problem specific information:                                            
                                                                         
n = 3408489886335277144344023699527218196631767672957 (162-bits)         
passes primality test, n is composite, continuing...                     
1) Initial bound: 80000, pi(80000) estimate: 7086,                       
    largest found: 71549 (actual bound)                                  
2) Number of quadratic residues estimate: 4725, actual number found: 3596
3) Modular square roots found: 7192(2x residues)                         
4) Constructing smooth number list [sieving] (can take a while)...       
Sieving for: 3606                                                        
5. Constructing a matrix of size: 3606x3597                              
Set a total of 37118 exponents, with 1815 negatives                      
Matrix solution found with: 1474 combinations                            
Divisor: 1816046478796474796528999 (probably prime)                      
Divisor: 1876873706775468629074043 (probably prime)                      

Ordering statistics:	result
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	1,707,729
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	1,647,739

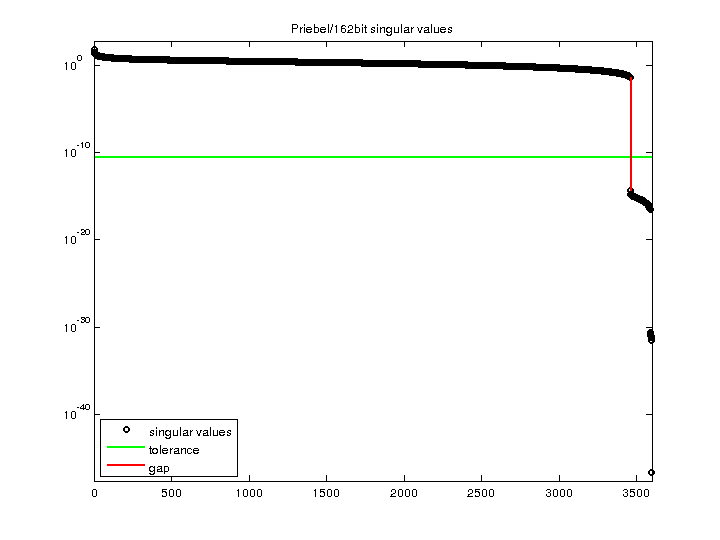
SVD-based statistics:
norm(A)	58.8077
min(svd(A))	0
cond(A)	Inf
rank(A)	3,460
sprank(A)-rank(A)	0
null space dimension	137
full numerical rank?	no
singular value gap	8.11879e+12

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.