Matrix: Pajek/EAT_SR
Description: Pajek network: Edinburgh Associative Thesaurus (stimulus-response)
 |
 |
| (bipartite graph drawing) | (graph drawing of A+A') |
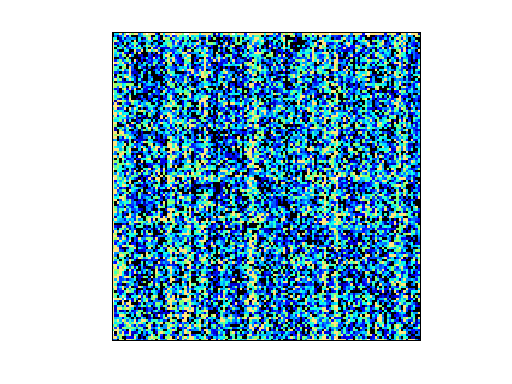 |
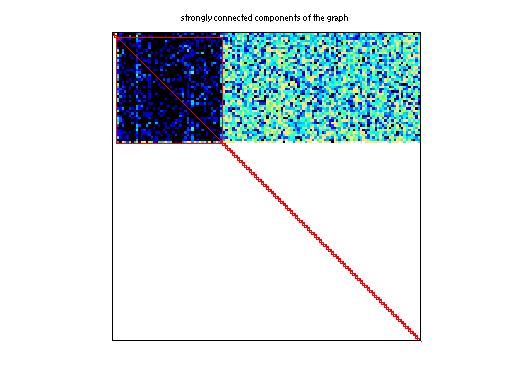 |
| Matrix properties | |
| number of rows | 23,219 |
| number of columns | 23,219 |
| nonzeros | 325,589 |
| # strongly connected comp. | 15,466 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | 12% |
| numeric value symmetry | 3% |
| type | integer |
| structure | unsymmetric |
| Cholesky candidate? | no |
| positive definite? | no |
| author | G. Kiss, C. Armstrong R. Milroy, J. Piper |
| editor | V. Batagelj |
| date | 1971 |
| kind | directed weighted graph |
| 2D/3D problem? | no |
| Additional fields | size and type |
| nodename | full 23219-by-20 |
Notes:
------------------------------------------------------------------------------
Pajek network converted to sparse adjacency matrix for inclusion in UF sparse
matrix collection, Tim Davis. For Pajek datasets, See V. Batagelj & A. Mrvar,
http://vlado.fmf.uni-lj.si/pub/networks/data/.
------------------------------------------------------------------------------
EAT - The Edinburgh Associative Thesaurus /
stimulus-response
--------------------------------------------------------
The EAT is a database of word association norms.
- Original EAT: George Kiss, Christine Armstrong,
Robert Milroy and J.R.I. Piper (1968-1971).
- MRC Psycholinguistic Database Version modified by:
Max Coltheart, S. James, J. Ramshaw, B.M. Philip,
B. Reid, J. Benyon-Tinker and E. Doctor;
made available by: Philip Quinlan.
- The present version was re-structured and documented
by Michael Wilson at the Rutherford Appleton Laboratory.
http://monkey.cis.rl.ac.uk/Eat/htdocs/eat.zip
transformed in Pajek format: V. Batagelj, 31. July 2003
-----
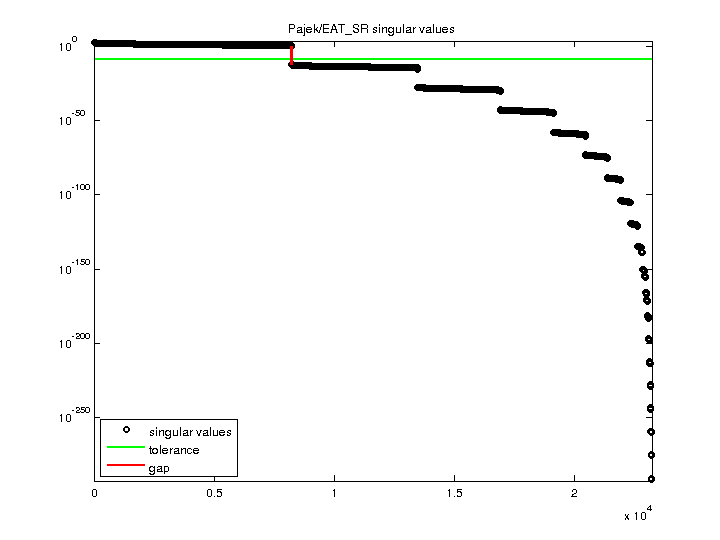
| SVD-based statistics: | |
| norm(A) | 312.442 |
| min(svd(A)) | 0 |
| cond(A) | Inf |
| rank(A) | 8,210 |
| null space dimension | 15,009 |
| full numerical rank? | no |
| singular value gap | 1.66891e+12 |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (A)) |
| status: | ok |
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.