
Matrix: MathWorks/QRpivot
Description: Limitation of basic solution to x=A\b using qr(A); needs min 2-norm
 |
| (bipartite graph drawing) |
 |
 |
| Matrix properties | |
| number of rows | 660 |
| number of columns | 749 |
| nonzeros | 3,808 |
| structural full rank? | yes |
| structural rank | 660 |
| # of blocks from dmperm | 9 |
| # strongly connected comp. | 1 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | 0% |
| numeric value symmetry | 0% |
| type | real |
| structure | rectangular |
| Cholesky candidate? | no |
| positive definite? | no |
| author | P. Quillen |
| editor | T. Davis |
| date | 2008 |
| kind | counter-example problem |
| 2D/3D problem? | no |
| Additional fields | size and type |
| b | sparse 660-by-1 |
Notes:
Counter-example problem from The MathWorks, Pat Quillen
This matrix was obtained from a MATLAB user. It illustrates the
limitations inherent in computing a basic solution to an under-
determined system without the use of column pivoting.
With column pivoting (which can only be done in MATLAB with full
matrices) the problem is solved properly.
When finding the min 2-norm solution (ignoring fill-in):
[Q,R] = qr (A') ;
x = Q*(R'\b) ;
a good solution is found. To reduce fill-in:
p = colamd (A') ;
[Q,R] = qr (A (p,:)') ;
x = Q*(R'\b(p)) ;
which also finds a good solution.
However, x=A\b computes a basic solution, using this algorithm:
q = colamd (A) ;
[Q,R] = qr (A (:,q)) ;
x = R\(Q'*b) ;
x (q) = q ;
which finds an error with norm(A*x-b) of 1e-9 in MATLAB 7.6.
With random permutations, and determining the cond(R1) of the leading
trianglar part (R is "squeezed" and the columns can be partitioned into
[R1 R2] where R1 is square and upper triangular) leads to the following
results.
Note that the error is high when condest(R1) is high. Note in
particular the last trial.
So this clinches the question. MATLAB's QR, and my new sparse QR, both
use a rank-detection method (by Heath) that does not do column pivoting,
and which is known to fail for some problems - for which Grimes & Lewis'
method will likely succeed.
The advantage of my QR is that I now always return R as upper
trapezoidal, so if the user is concerned, he/she can easily check
condest(R(:,1:m)) if m < n.
err 7.71e-07 condest R1 2.18e+12
err 1.25e-09 condest R1 9.82e+08
err 2.47e-09 condest R1 2.46e+11
err 4.00e-09 condest R1 4.03e+09
err 9.88e-10 condest R1 4.73e+09
err 2.25e-08 condest R1 5.34e+09
err 2.00e-08 condest R1 1.04e+09
err 1.09e-09 condest R1 6.83e+08
err 6.18e-08 condest R1 8.13e+10
err 3.13e-10 condest R1 4.23e+09
err 6.64e-10 condest R1 2.46e+10
err 5.76e-09 condest R1 4.31e+09
err 7.61e-07 condest R1 5.08e+10
err 2.27e-09 condest R1 4.94e+09
err 3.99e-10 condest R1 2.80e+09
err 1.37e-09 condest R1 3.13e+09
err 6.93e-05 condest R1 1.84e+14
err 1.35e-08 condest R1 7.18e+09
err 1.09e-08 condest R1 1.79e+11
err 1.81e-09 condest R1 2.99e+08
err 1.55e-01 condest R1 2.45e+18
In summary, this is a "feature" not a "bug". If you want a reliable
solution to an underdetermined system, find the min 2norm solution
via a QR factorization of A'.
| Ordering statistics: | result |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 15,330 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 15,836 |
| SVD-based statistics: | |
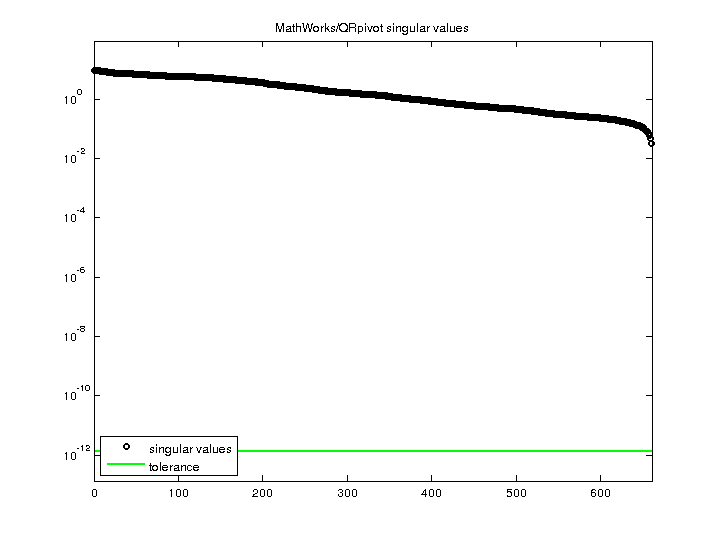
| norm(A) | 9.33232 |
| min(svd(A)) | 0.0320586 |
| cond(A) | 291.102 |
| rank(A) | 660 |
| sprank(A)-rank(A) | 0 |
| null space dimension | 0 |
| full numerical rank? | yes |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (A)) ; |
| status: | ok |
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.