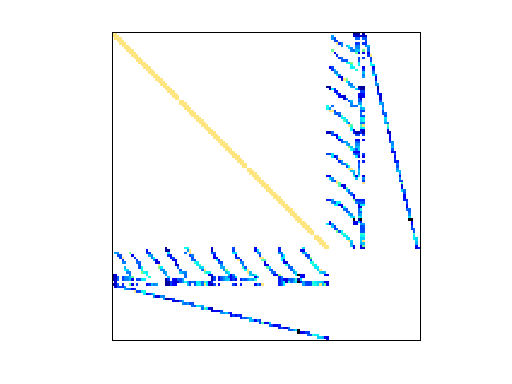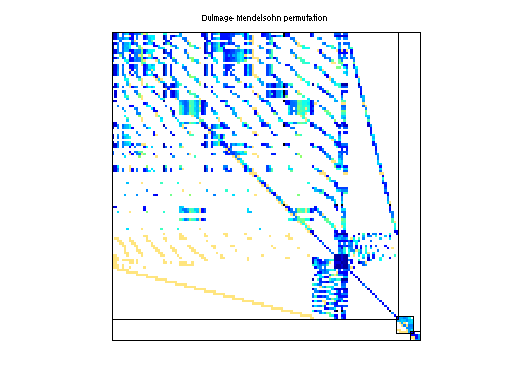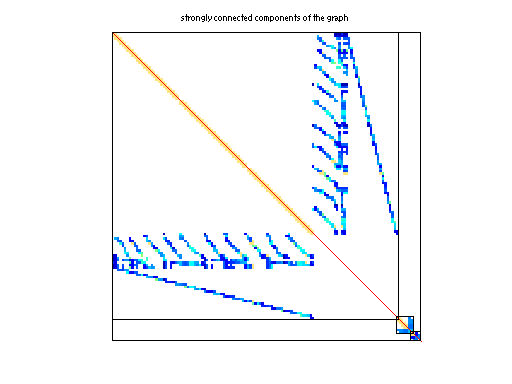Matrix properties
number of rows	7,245
number of columns	7,245
nonzeros	46,142
structural full rank?	yes
structural rank	7,245
# of blocks from dmperm	3
# strongly connected comp.	3
explicit zero entries	0
nonzero pattern symmetry	symmetric
numeric value symmetry	symmetric
type	real
structure	symmetric
Cholesky candidate?	no
positive definite?	no

author	T. Di Fonzo, M. Marini
editor	T. Davis
date	2008
kind	economic problem
2D/3D problem?	no

Additional fields	size and type
b	full 7245-by-1

Notes:

Economic statistics are often published in the form of time series, as a   
collection of observations sampled at equally-spaced time periods (months, 
quarters). Economic concepts behind such statistics are often linked by a  
system of linear relationships, deriving from the economic theory. However,
these restrictions are rarely met by the original time series for various  
reasons.  Then, data sets of real-world variables generally show           
discrepancies with respect to prior restrictions on their values.  The     
adjustment of a set of data in order to satisfy a number of accounting     
restrictions -and thus to remove any discrepancy -is generally known as    
the reconciliation problem.                                                
                                                                           
The matrix comes from a real application composed of 183 quarterly time    
series observed over 28 quarters, which form the system of European        
national accounts by institutional sectors (EURQSA). Then, the number of   
observations to be reconciled is n = 28 x 183 = 5124. The variables are    
connected by a system of 30 linear relationships. Moreover, each quarterly 
time series must be in line with the same variables observed yearly (due   
to different compilation practices quarterly and annual estimates might    
differ). The total number of constraints of the system is k = 2121. On     
the whole, matrix A has dimension 7245, with block (1,1) of dimension 5124.

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	153,155
Cholesky flop count	1.3e+07
nnz(L+U), no partial pivoting, with AMD	299,065
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	1,174,854
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	2,203,468

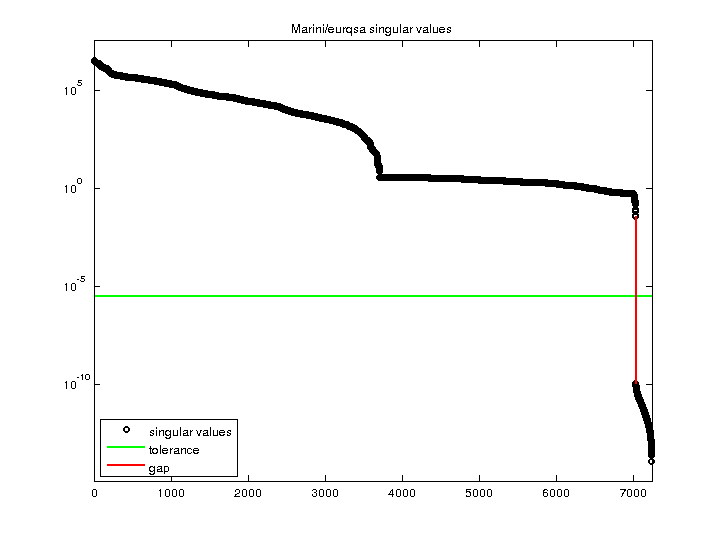
SVD-based statistics:
norm(A)	3.47577e+06
min(svd(A))	1.23888e-14
cond(A)	2.80557e+20
rank(A)	7,035
sprank(A)-rank(A)	210
null space dimension	210
full numerical rank?	no
singular value gap	3.03054e+08

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.