Matrix properties
number of rows	1,388
number of columns	390
nonzeros	11,816
structural full rank?	yes
structural rank	390
# of blocks from dmperm	1
# strongly connected comp.	1
explicit zero entries	0
nonzero pattern symmetry	0%
numeric value symmetry	0%
type	real
structure	rectangular
Cholesky candidate?	no
positive definite?	no

author	B. Luong
editor	T. Davis
date	2008
kind	computer graphics/vision problem
2D/3D problem?	yes

Additional fields	size and type
b	full 1388-by-1

Notes:

Photogrammetry problem from Bruno Luong, FOGALE nanotech, France.     
The problem of interest is:                                           
    [U S V]=svd(full(A),0);                                           
    s=diag(S);                                                        
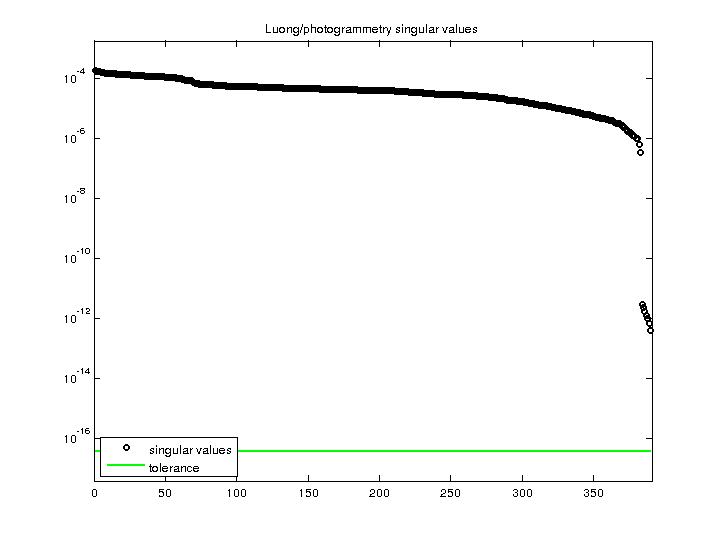
The spectrum has two parts:                                           
- the singular values s(1) to s(end-7) are 1.7486e-004 to 3.4655e-007 
(ratio 504.57).                                                       
- the singular values s(end-6) to s(end) is smaller than 2.9614e-012  
(ratio > 5.9e7).                                                      
So in this problem, the following are considered:                     
K = span is the kernel of A, and                     
L = span = orthogonal(K) is isomorph to Im(A).         

Ordering statistics:	result
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	212,121
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	33,931

SVD-based statistics:
norm(A)	0.000174861
min(svd(A))	4.01803e-13
cond(A)	4.35191e+08
rank(A)	390
sprank(A)-rank(A)	0
null space dimension	0
full numerical rank?	yes

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.