Matrix: LPnetlib/lpi_itest2
Description: Netlib LP problem itest2: minimize c'*x, where Ax=b, lo<=x<=hi
 |
| (bipartite graph drawing) |
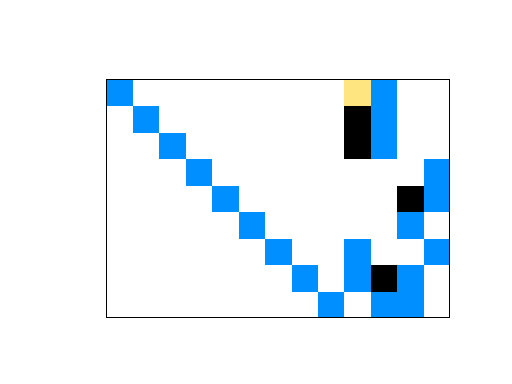 |
| Matrix properties | |
| number of rows | 9 |
| number of columns | 13 |
| nonzeros | 26 |
| structural full rank? | yes |
| structural rank | 9 |
| # of blocks from dmperm | 1 |
| # strongly connected comp. | 1 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | 0% |
| numeric value symmetry | 0% |
| type | real |
| structure | rectangular |
| Cholesky candidate? | no |
| positive definite? | no |
| author | J. Chinneck, E. Dravnieks |
| editor | J. Chinneck |
| date | 1991 |
| kind | linear programming problem |
| 2D/3D problem? | no |
| Additional fields | size and type |
| b | full 9-by-1 |
| c | full 13-by-1 |
| lo | full 13-by-1 |
| hi | full 13-by-1 |
| z0 | full 1-by-1 |
Notes:
An infeasible Netlib LP problem, in lp/infeas. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/infeas
The lp/infeas directory contains infeasible linear programming test problems
collected by John W. Chinneck, Carleton Univ, Ontario Canada. The following
are relevant excerpts from lp/infeas/readme (by John W. Chinneck):
In the following, IIS stands for Irreducible Infeasible Subsystem, a set
of constraints which is itself infeasible, but becomes feasible when any
one member is removed. Isolating an IIS from within the larger set of
constraints defining the model is one analysis approach.
PROBLEM DESCRIPTION
-------------------
ITEST6, ITEST2: very small problems having numerous clustered IISs.
These match problems 1 and 2, respectively, in Chinneck and Dravnieks
[1991]. Contributors: J.W. Chinneck and E.W. Dravnieks, Carleton
University.
Name Rows Cols Nonzeros Bounds Notes
itest2 10 4 17
REFERENCES
----------
J.W. Chinneck and E.W. Dravnieks (1991). "Locating Minimal Infeasible
Constraint Sets in Linear Programs", ORSA Journal on Computing, Volume
3, No. 2.
| Ordering statistics: | result |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 36 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 32 |
| SVD-based statistics: | |
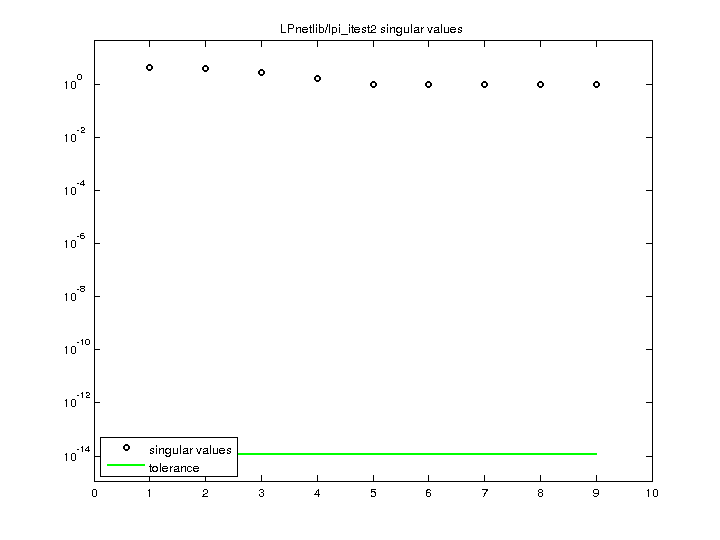
| norm(A) | 4.22605 |
| min(svd(A)) | 1 |
| cond(A) | 4.22605 |
| rank(A) | 9 |
| sprank(A)-rank(A) | 0 |
| null space dimension | 0 |
| full numerical rank? | yes |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (R)) ; where [~,R,E] = spqr (A') with droptol of zero |
| status: | ok |
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.