Matrix: LPnetlib/lpi_cplex2
Description: Netlib LP problem cplex2: minimize c'*x, where Ax=b, lo<=x<=hi
 |
| (bipartite graph drawing) |
 |
| Matrix properties | |
| number of rows | 224 |
| number of columns | 378 |
| nonzeros | 1,215 |
| structural full rank? | yes |
| structural rank | 224 |
| # of blocks from dmperm | 1 |
| # strongly connected comp. | 1 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | 0% |
| numeric value symmetry | 0% |
| type | real |
| structure | rectangular |
| Cholesky candidate? | no |
| positive definite? | no |
| author | E. Klotz |
| editor | J. Chinneck |
| date | 1993 |
| kind | linear programming problem |
| 2D/3D problem? | no |
| Additional fields | size and type |
| b | full 224-by-1 |
| c | full 378-by-1 |
| lo | full 378-by-1 |
| hi | full 378-by-1 |
| z0 | full 1-by-1 |
Notes:
An infeasible Netlib LP problem, in lp/infeas. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/infeas
The lp/infeas directory contains infeasible linear programming test problems
collected by John W. Chinneck, Carleton Univ, Ontario Canada. The following
are relevant excerpts from lp/infeas/readme (by John W. Chinneck):
In the following, IIS stands for Irreducible Infeasible Subsystem, a set
of constraints which is itself infeasible, but becomes feasible when any
one member is removed. Isolating an IIS from within the larger set of
constraints defining the model is one analysis approach.
PROBLEM DESCRIPTION
-------------------
CPLEX1, CPLEX2: medium and large problems respectively. CPLEX1
referred to as CPLEX problem in Chinneck [1993], and is remarkably
non-volatile, showing a single small IIS regardless of the IIS algorithm
applied. CPLEX2 is an almost-feasible problem. Contributor: Ed Klotz,
CPLEX Optimization Inc.
Name Rows Cols Nonzeros Bounds Notes
cplex2 225 221 1059 B
REFERENCES
----------
J.W. Chinneck (1993). "Finding the Most Useful Subset of Constraints
for Analysis in an Infeasible Linear Program", technical report
SCE-93-07, Systems and Computer Engineering, Carleton University,
Ottawa, Canada.
| Ordering statistics: | result |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 5,305 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 2,167 |
| SVD-based statistics: | |
| norm(A) | 15.5552 |
| min(svd(A)) | 7.69642e-17 |
| cond(A) | 2.02109e+17 |
| rank(A) | 223 |
| sprank(A)-rank(A) | 1 |
| null space dimension | 1 |
| full numerical rank? | no |
| singular value gap | 4.37093e+14 |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (A)) ; |
| status: | ok |
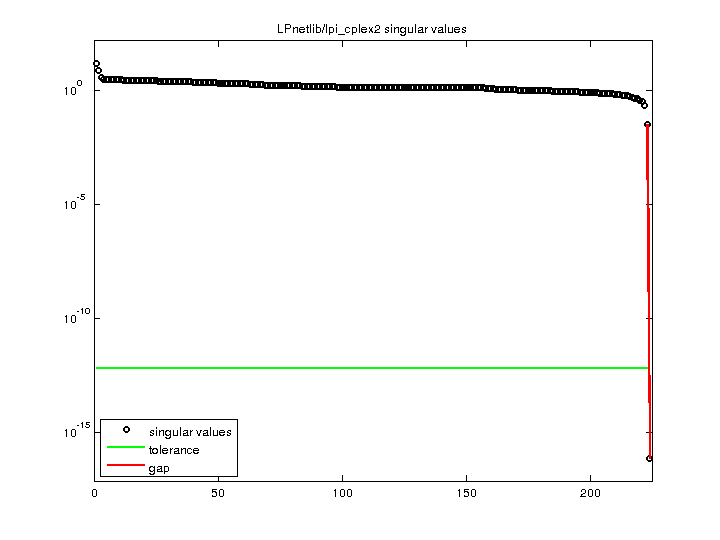
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.