Matrix: LPnetlib/lp_qap15
Description: Netlib LP problem qap15: minimize c'*x, where Ax=b, lo<=x<=hi
 |
| (bipartite graph drawing) |
 |
| Matrix properties | |
| number of rows | 6,330 |
| number of columns | 22,275 |
| nonzeros | 94,950 |
| structural full rank? | yes |
| structural rank | 6,330 |
| # of blocks from dmperm | 1 |
| # strongly connected comp. | 1 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | 0% |
| numeric value symmetry | 0% |
| type | integer |
| structure | rectangular |
| Cholesky candidate? | no |
| positive definite? | no |
| author | T. Johnson |
| editor | R. Bixby, M. Saltzman, T. Johnson |
| date | |
| kind | linear programming problem |
| 2D/3D problem? | no |
| Additional fields | size and type |
| b | full 6330-by-1 |
| c | full 22275-by-1 |
| lo | full 22275-by-1 |
| hi | full 22275-by-1 |
| z0 | full 1-by-1 |
Notes:
A Netlib LP problem, in lp/generators/qap. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/data
send readme from lp/generators/qap
This copy of QAP15 was created by the QAP generator program,
on an Sun UltraSparc, on May 15, 1997.
The following are relevant excerpts from lp/data/readme (by David M. Gay):
The column and nonzero counts in the PROBLEM SUMMARY TABLE below exclude
slack and surplus columns and the right-hand side vector, but include
the cost row. We have omitted other free rows and all but the first
right-hand side vector, as noted below. The byte count is for the
MPS compressed file; it includes a newline character at the end of each
line. These files start with a blank initial line intended to prevent
mail programs from discarding any of the data. The BR column indicates
whether a problem has bounds or ranges: B stands for "has bounds", R
for "has ranges".
The optimal value is from MINOS version 5.3 (of Sept. 1988)
running on a VAX with default options.
PROBLEM SUMMARY TABLE
Name Rows Cols Nonzeros Bytes BR Optimal Value
QAP15 6331 22275 110700 (see NOTES) 1.0409940410E+03
Problems QAP8, QAP12, and QAP15 are from a generator by Terri
Johnson (communicated by a combination of Bob Bixby, Matt Saltzman, and
Terri Johnson).
Source for Terri Johnson's generator and input data
for producing MPS files for QAP8, QAP12, and QAP15 appear in directory
lp/generators/qap.
Added to Netlib on 12 April 1996.
The following are relevant excerpts from lp/generators/qap/readme
(by Terri Johnson):
The Quadratic Assignment Problem (Problem QAP) is a specially-
structured zero-one quadratic programming problem. While having
received considerable attention since its introduction into the
literature over 30 years ago, and while many applications exist in
various disciplines, this problem has resisted exact solution
procedures. Only for smaller-size problems can optimal solutions be
obtained and verified. The solution strategies for Problem QAP
developed by Johnson (Ph.D. dissertation, Clemson University, 1992)
and Adams and Johnson (Improved Linear Programming-based Lower Bounds
for the Quadratic Assignment Problem, DIMACS: Quadratic Assignment
and Related Problems, Vol. 16 (1994), 43-75) are based on a new,
equivalent, mixed- integer linear reformulation, Problem LP.
The traditional , nonlinear formulation of Problem QAP has a
quadratic objective function, 2m constraints and m^2 binary variables.
The linearized version of concern, Problem LP, on the other hand, has
2m^2(m-1) + m^2(m-1)^2/2 + 2m constraints, in addition to non-
negativity restrictions on all the variables, and m^2 binary variables
and m^2(m-1)^2 continuous variables. The continuous relaxation of
Problem LP, obtained by omitting the x binary restrictions, possesses
a special block diagonal structure which readily lends itself to
decomposition techniques. However, the inherent degeneracy makes this
a formidable program for problems as small in size as m=15 to 20. A
smaller reformulation, which reduces the number of constraints and
variables each by m^2(m-1)^2/2, can be obtained via an appropriate
substitution of variables, but such a substitution forfeits the
problem structure. It has been amply demonstrated that this
formulation serves as a unifying and dominating entity with respect to
the different linear reformulations of Problem QAP, as well as with
respect to a variety of bounding procedures. Consequently, the
ability to quickly solve this linear formulation holds the promise of
being able to solve larger-sized QAP's.
Provided here is Fortran source, newlp.f, for a program that
generates MPS files for the linearized QAP with the substitution of
variables. Under the assumption that the test problem is symmetric,
the generator reads the problem size, m, and an mxm matrix with the
original distances in the upper half of the matrix and the original
flows in the lower half of the matrix. All diagonal entries are 0.
Using this input, the generator program computes the objective
function coefficients for the quadratic terms, and automatically
computes the constraints. The objective function is assumed to
contain no linear terms since such values can be easily incorporated
into the quadratic terms.
Input files qap8.dat, qap12.dat, and qap15.dat cause the
generator program to emit MPS files for well-known test problems of
Nugent, C.E., T.E. Vollmann, and J. Ruml, An Experimental Comparison
of Techniques for the Assignment of Facilities to Locations,
Operations Research, Vol. 16, No. 1 (1968), 150-173, of sizes m=8, 12,
and 15 for the linearization.
PROBLEM: M = 15 No. of Variables No. of Constraints
QAP 225 30
LP (with substitution) 22275 6330
Optimal value: 1.0409940410e+3
For more information, please contact Terri Johnson at:
johnsont@numen.elon.edu
| Ordering statistics: | result |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 72,888,252 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 9,342,598 |
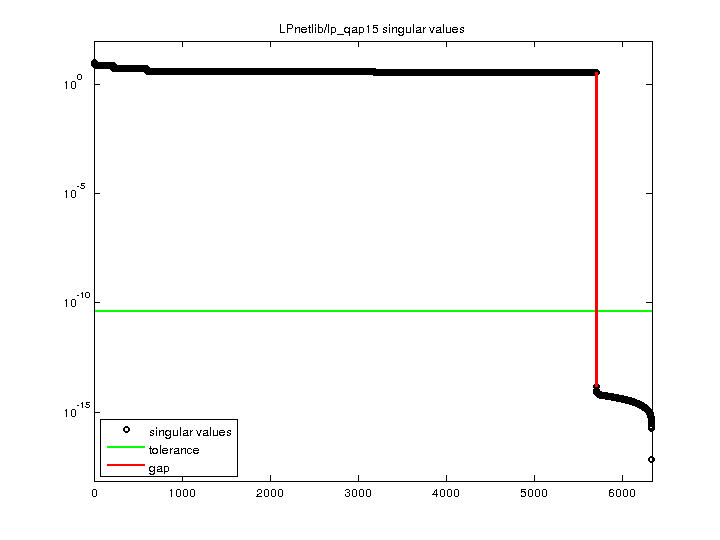
| SVD-based statistics: | |
| norm(A) | 9.82907 |
| min(svd(A)) | 7.04198e-18 |
| cond(A) | 1.39578e+18 |
| rank(A) | 5,698 |
| sprank(A)-rank(A) | 632 |
| null space dimension | 632 |
| full numerical rank? | no |
| singular value gap | 2.50747e+14 |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (R)) ; where [~,R,E] = spqr (A') with droptol of zero |
| status: | ok |
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.