Matrix properties
number of rows	1,441
number of columns	4,860
nonzeros	44,375
structural full rank?	yes
structural rank	1,441
# of blocks from dmperm	2
# strongly connected comp.	1
explicit zero entries	0
nonzero pattern symmetry	0%
numeric value symmetry	0%
type	real
structure	rectangular
Cholesky candidate?	no
positive definite?	no

author	M. Saunders
editor	D. Gay
date	1989
kind	linear programming problem
2D/3D problem?	no

Additional fields	size and type
b	full 1441-by-1
c	full 4860-by-1
lo	full 4860-by-1
hi	full 4860-by-1
z0	full 1-by-1

Notes:

A Netlib LP problem, in lp/data.  For more information                        
send email to netlib@ornl.gov with the message:                               
                                                                              
	 send index from lp                                                          
	 send readme from lp/data                                                    
	 send minos from lp/data                                                     
                                                                              
The following are relevant excerpts from lp/data/readme (by David M. Gay):    
                                                                              
The column and nonzero counts in the PROBLEM SUMMARY TABLE below exclude      
slack and surplus columns and the right-hand side vector, but include         
the cost row.  We have omitted other free rows and all but the first          
right-hand side vector, as noted below.  The byte count is for the            
MPS compressed file; it includes a newline character at the end of each       
line.  These files start with a blank initial line intended to prevent        
mail programs from discarding any of the data.  The BR column indicates       
whether a problem has bounds or ranges:  B stands for "has bounds", R         
for "has ranges".  The BOUND-TYPE TABLE below shows the bound types           
present in those problems that have bounds.                                   
                                                                              
The optimal value is from MINOS version 5.3 (of Sept. 1988)                   
running on a VAX with default options.                                        
                                                                              
                       PROBLEM SUMMARY TABLE                                  
                                                                              
Name       Rows   Cols   Nonzeros    Bytes  BR      Optimal Value             
PILOT      1442   3652    43220     278593  B    -5.5740430007E+02            
                                                                              
        BOUND-TYPE TABLE                                                      
PILOT      UP LO FX                                                           
                                                                              
From Michael Saunders, Systems Optimization Laboratory at Stanford University.
When included in Netlib: Extra bound sets omitted;                            
cost coefficients negated.                                                    
                                                                              
Bob Bixby reports that the CPLEX solver (running on a Sparc station)          
finds slightly different optimal values for some of the problems.             
On a MIPS processor, MINOS version 5.3 (with crash and scaling of             
December 1989) also finds different optimal values for some of the            
problems.  The following table shows the values that differ from those        
shown above.  (Whether CPLEX finds different values on the recently           
added problems remains to be seen.)                                           
                                                                              
Problem        CPLEX(Sparc)          MINOS(MIPS)                              
PILOT       -5.5748972928E+02    -5.5741215293E+02                            
                                                                              
Concerning PILOT87, Irv Lustig says, "PILOT87 is considered (by John          
Stone, at least) to be harder than PILOT because of the bad scaling in        
the numerics."                                                                
                                                                              
Modified on Oct. 1991 (minor cleanup): removed 8 duplicate right-hand         
side values for row BTRB01.                                                   
                                                                              
The following are relevant excerts from lp/data/minos (by Michael Saunders),  
regarding experience with MINOS 5.0 on the problems he provided:              
                                                                              
                                                     (unscaled)   (scaled)    
File   Name    Rows  Cols  Elems  Optimal Objective  Itns  Time  Itns  Time   
---- --------  ----  ----  -----  -----------------  ----  ----  ----  ----   
 13. PILOT     1460  3652  43645  5.5742994E+02 MAX    ?     ?  20000* 2hrs*  
                                                                              
* Objective  is the first row of type N.  It is minimized except as shown.    
                                                                              
* Itns       is the number of iterations required to solve the problem        
             by the primal simplex method, as implemented in the Fortran      
             code MINOS 5.0 (May 1985), using default values for all          
             parameters.  (The initial basis is triangular.)                  
                                                                              
* Time       is the processor time required on an IBM 3081K.  The MINOS       
             source code was compiled with the IBM Fortran 77 compiler        
             VS FORTRAN, using the options NOSDUMP, NOSYM and OPT(3).         
                                                                              
* PILOT      is a linearized form of a quadratic program.  The first 45       
             objective elements are the optimal gradients of the quadratic    
             terms in the objective of the QP.  PILOT is normally solved      
             from an advanced basis, with scaling.  The Itns and Time shown   
             above are estimates.                                             
                                                                              

Ordering statistics:	result
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	1,367,157
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	180,661

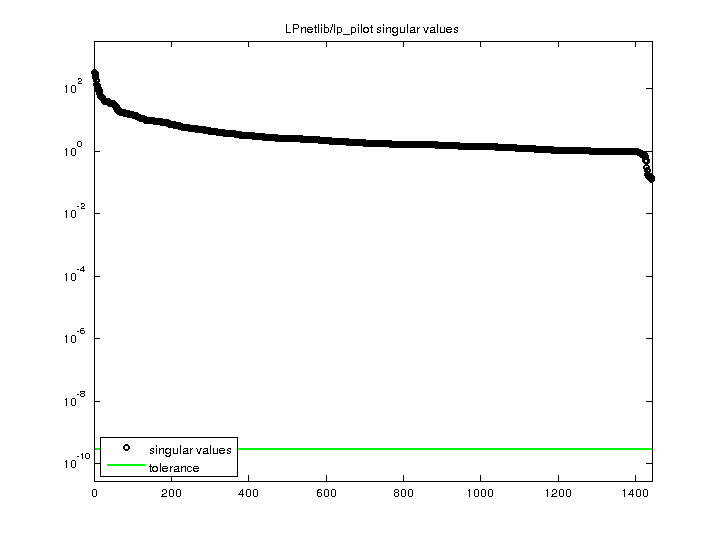
SVD-based statistics:
norm(A)	331.71
min(svd(A))	0.124612
cond(A)	2661.95
rank(A)	1,441
sprank(A)-rank(A)	0
null space dimension	0
full numerical rank?	yes

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.