Matrix: LPnetlib/lp_osa_60
Description: Netlib LP problem osa_60: minimize c'*x, where Ax=b, lo<=x<=hi
 |
| (bipartite graph drawing) |
 |
| Matrix properties | |
| number of rows | 10,280 |
| number of columns | 243,246 |
| nonzeros | 1,408,073 |
| structural full rank? | yes |
| structural rank | 10,280 |
| # of blocks from dmperm | 1 |
| # strongly connected comp. | 1 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | 0% |
| numeric value symmetry | 0% |
| type | real |
| structure | rectangular |
| Cholesky candidate? | no |
| positive definite? | no |
| author | J. Kennington |
| editor | I. Lustig |
| date | 1990 |
| kind | linear programming problem |
| 2D/3D problem? | no |
| Additional fields | size and type |
| b | full 10280-by-1 |
| c | full 243246-by-1 |
| lo | full 243246-by-1 |
| hi | full 243246-by-1 |
| z0 | full 1-by-1 |
Notes:
A Netlib LP problem, in lp/data/kennington. For more information
send email to netlib@ornl.gov with the message:
send index from lp
send readme from lp/data
send readme from lp/data/kennington
The following are relevant excerpts from lp/data/kennington/readme:
The "Kennington" problems: sixteen problems described in "An Empirical
Evaluation of the KORBX Algorithms for Military Airlift Applications"
by W. J. Carolan, J. E. Hill, J. L. Kennington, S. Niemi, S. J.
Wichmann (Operations Research vol. 38, no. 2 (1990), pp. 240-248).
The following table gives some statistics for the "Kennington"
problems. The number of columns excludes slacks and surpluses.
The bounds column tells how many entries appear in the BOUNDS
section of the MPS file. The mpc column shows the bytes in
the problem after "uncompress" and before "emps"; MPS shows
the bytes after "emps". The optimal values were computed by
Vanderbei's ALPO, running on an SGI computer (with binary IEEE
arithmetic).
Name rows columns nonzeros bounds mpc MPS optimal value
OSA-60 10281 232966 1630758 0 10377094 52402461 4.0440725e+06
Submitted to Netlib by Irv Lustig.
| Ordering statistics: | result |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 19,114,532 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 515,735 |
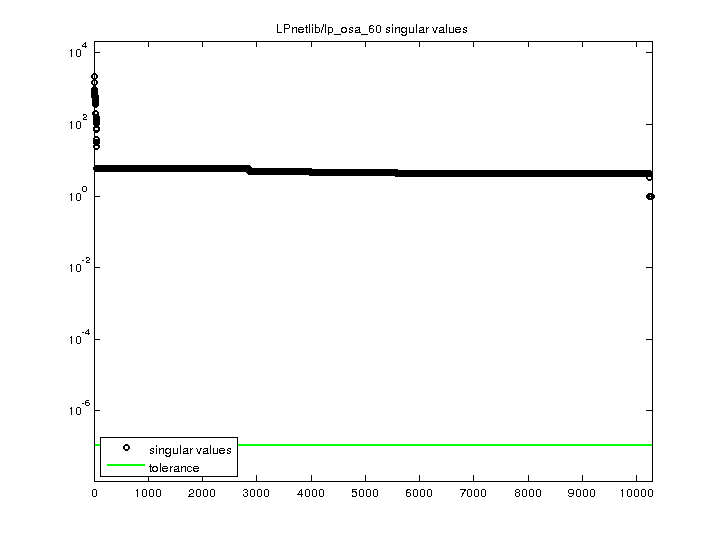
| SVD-based statistics: | |
| norm(A) | 2138.5 |
| min(svd(A)) | 1 |
| cond(A) | 2138.5 |
| rank(A) | 10,280 |
| sprank(A)-rank(A) | 0 |
| null space dimension | 0 |
| full numerical rank? | yes |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (R)) ; where [~,R,E] = spqr (A') with droptol of zero |
| status: | ok |
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.