Matrix properties
number of rows	20
number of columns	20
nonzeros	158
structural full rank?	yes
structural rank	20
# of blocks from dmperm	1
# strongly connected comp.	1
explicit zero entries	0
nonzero pattern symmetry	symmetric
numeric value symmetry	symmetric
type	integer
structure	symmetric
Cholesky candidate?	yes
positive definite?	yes

author	N. Trefethen
editor	J.-G. Dumas
date	2008
kind	combinatorial problem
2D/3D problem?	no

Notes:

Diagonal matrices with primes, Nick Trefethen, Oxford Univ.          
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,         
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html            
                                                                     
Problem 7 of the Hundred-dollar, Hundred-digit Challenge Problems,   
SIAM News, vol 35, no. 1.                                            
                                                                     
7. Let A be the 20,000 x 20,000 matrix whose entries are zero        
everywhere except for the primes 2, 3, 5, 7, . . . , 224737 along the
main diagonal and the number 1 in all the positions A(i,j) with      
|i-j| = 1,2,4,8, . . . ,16384.  What is the (1,1) entry of inv(A)?   
                                                                     
http://www.siam.org/news/news.php?id=388                             
                                                                     
Filename in JGD collection: Trefethen/trefethen_20.sms               

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	147
Cholesky flop count	1.3e+03
nnz(L+U), no partial pivoting, with AMD	274
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	174
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	207

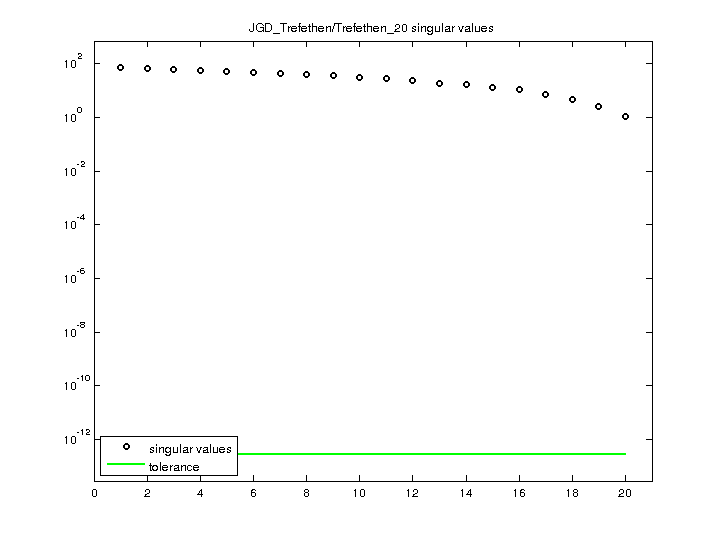
SVD-based statistics:
norm(A)	71.5124
min(svd(A))	1.13352
cond(A)	63.0886
rank(A)	20
sprank(A)-rank(A)	0
null space dimension	0
full numerical rank?	yes

singular values (MAT file):	click here
SVD method used:	s = svd (full (A))
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.