Matrix properties
number of rows	6,545
number of columns	6,545
nonzeros	295,680
structural full rank?	yes
structural rank	6,545
# of blocks from dmperm	1
# strongly connected comp.	1
explicit zero entries	0
nonzero pattern symmetry	symmetric
numeric value symmetry	symmetric
type	binary
structure	symmetric
Cholesky candidate?	no
positive definite?	no

author	G. Royle
editor	J.-G. Dumas
date	2008
kind	combinatorial problem
2D/3D problem?	no

Notes:

Symmetric powers of graphs from Gordon Royle, Univ Western Australia
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,        
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html           
                                                                    
http://www.csse.uwa.edu.au/~gordon/sympower.html                    
                                                                    
Filename in JGD collection: SPG/EX6.sms                             

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	15,203,059
Cholesky flop count	5.5e+10
nnz(L+U), no partial pivoting, with AMD	30,399,573
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	19,253,430
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	20,660,929

SVD-based statistics:
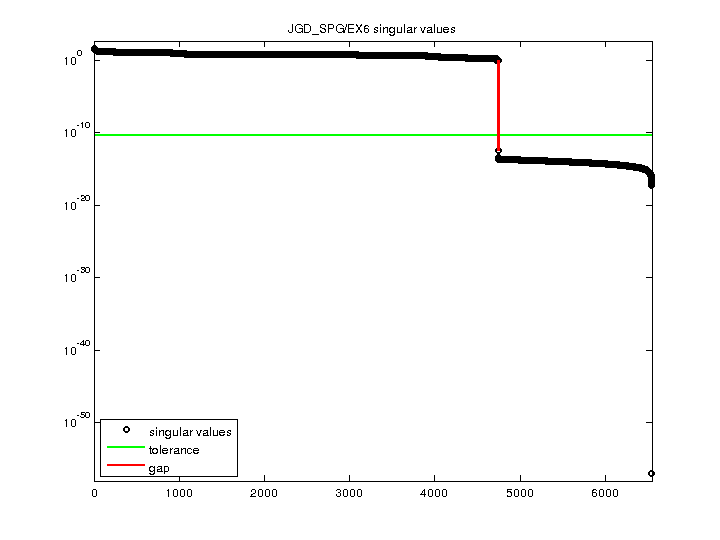
norm(A)	45.2591
min(svd(A))	8.50982e-58
cond(A)	5.31846e+58
rank(A)	4,740
sprank(A)-rank(A)	1,805
null space dimension	1,805
full numerical rank?	no
singular value gap	2.5302e+12

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.