
Matrix: JGD_Margulies/wheel_6_1
Description: Combinatorial optimization as polynomial eqns, Susan Margulies, UC Davis
 |
| (bipartite graph drawing) |
 |
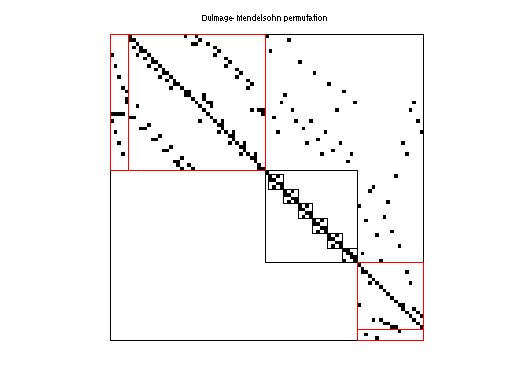 |
| Matrix properties | |
| number of rows | 83 |
| number of columns | 85 |
| nonzeros | 254 |
| structural full rank? | no |
| structural rank | 80 |
| # of blocks from dmperm | 9 |
| # strongly connected comp. | 1 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | 0% |
| numeric value symmetry | 0% |
| type | binary |
| structure | rectangular |
| Cholesky candidate? | no |
| positive definite? | no |
| author | S. Margulies |
| editor | J.-G. Dumas |
| date | 2008 |
| kind | combinatorial problem |
| 2D/3D problem? | no |
Notes:
Combinatorial optimization as polynomial eqns, Susan Margulies, UC Davis
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html
http://arxiv.org/abs/0706.0578
Expressing Combinatorial Optimization Problems by Systems of Polynomial
Equations and the Nullstellensatz
Authors: J.A. De Loera, J. Lee, Susan Margulies, S. Onn
(Submitted on 5 Jun 2007)
Abstract: Systems of polynomial equations over the complex or real
numbers can be used to model combinatorial problems. In this way, a
combinatorial problem is feasible (e.g. a graph is 3-colorable,
hamiltonian, etc.) if and only if a related system of polynomial
equations has a solution. In the first part of this paper, we construct
new polynomial encodings for the problems of finding in a graph its
longest cycle, the largest planar subgraph, the edge-chromatic number,
or the largest k-colorable subgraph. For an infeasible polynomial
system, the (complex) Hilbert Nullstellensatz gives a certificate that
the associated combinatorial problem is infeasible. Thus, unless P =
NP, there must exist an infinite sequence of infeasible instances of
each hard combinatorial problem for which the minimum degree of a
Hilbert Nullstellensatz certificate of the associated polynomial system
grows. We show that the minimum-degree of a Nullstellensatz
certificate for the non-existence of a stable set of size greater than
the stability number of the graph is the stability number of the graph.
Moreover, such a certificate contains at least one term per stable set
of G. In contrast, for non-3- colorability, we found only graphs with
Nullstellensatz certificates of degree four.
Filename in JGD collection: Margulies/wheel_6_1.sms
| Ordering statistics: | result |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 368 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 692 |
| SVD-based statistics: | |
| norm(A) | 3.58234 |
| min(svd(A)) | 6.71916e-17 |
| cond(A) | 5.33153e+16 |
| rank(A) | 72 |
| sprank(A)-rank(A) | 8 |
| null space dimension | 11 |
| full numerical rank? | no |
| singular value gap | 3.33314e+14 |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (A)) ; |
| status: | ok |
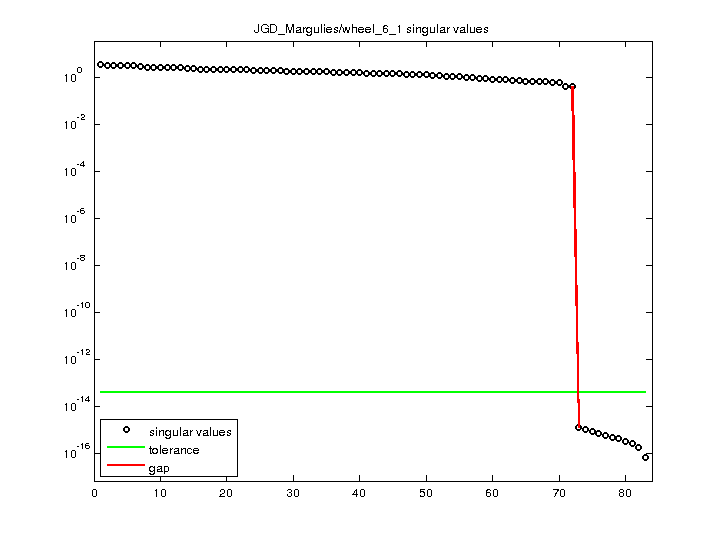
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.