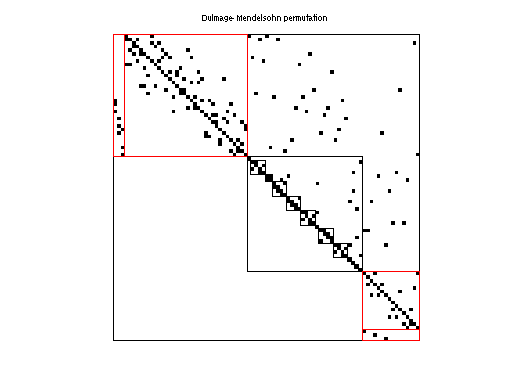Matrix properties
number of rows	85
number of columns	85
nonzeros	254
structural full rank?	no
structural rank	82
# of blocks from dmperm	15
# strongly connected comp.	1
explicit zero entries	0
nonzero pattern symmetry	3%
numeric value symmetry	3%
type	binary
structure	unsymmetric
Cholesky candidate?	no
positive definite?	no

author	S. Margulies
editor	J.-G. Dumas
date	2008
kind	combinatorial problem
2D/3D problem?	no

Notes:

Combinatorial optimization as polynomial eqns, Susan Margulies, UC Davis
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,            
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html               
                                                                        
http://arxiv.org/abs/0706.0578                                          
                                                                        
Expressing Combinatorial Optimization Problems by Systems of Polynomial 
Equations and the Nullstellensatz                                       
                                                                        
Authors: J.A. De Loera, J. Lee, Susan Margulies, S. Onn                 
                                                                        
(Submitted on 5 Jun 2007)                                               
                                                                        
Abstract: Systems of polynomial equations over the complex or real      
numbers can be used to model combinatorial problems. In this way, a     
combinatorial problem is feasible (e.g. a graph is 3-colorable,         
hamiltonian, etc.) if and only if a related system of polynomial        
equations has a solution. In the first part of this paper, we construct 
new polynomial encodings for the problems of finding in a graph its     
longest cycle, the largest planar subgraph, the edge-chromatic number,  
or the largest k-colorable subgraph.  For an infeasible polynomial      
system, the (complex) Hilbert Nullstellensatz gives a certificate that  
the associated combinatorial problem is infeasible. Thus, unless P =    
NP, there must exist an infinite sequence of infeasible instances of    
each hard combinatorial problem for which the minimum degree of a       
Hilbert Nullstellensatz certificate of the associated polynomial system 
grows.  We show that the minimum-degree of a Nullstellensatz            
certificate for the non-existence of a stable set of size greater than  
the stability number of the graph is the stability number of the graph. 
Moreover, such a certificate contains at least one term per stable set  
of G. In contrast, for non-3- colorability, we found only graphs with   
Nullstellensatz certificates of degree four.                            
                                                                        
Filename in JGD collection: Margulies/cat_ears_2_1.sms                  

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	1,045
Cholesky flop count	1.8e+04
nnz(L+U), no partial pivoting, with AMD	2,005
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	581
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	962

SVD-based statistics:
norm(A)	3.42573
min(svd(A))	7.71606e-18
cond(A)	4.43974e+17
rank(A)	74
sprank(A)-rank(A)	8
null space dimension	11
full numerical rank?	no
singular value gap	3.70665e+14

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

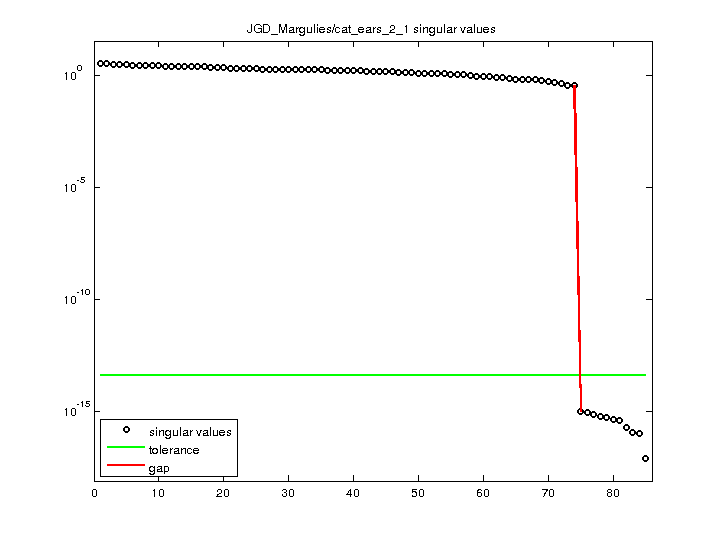
For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.