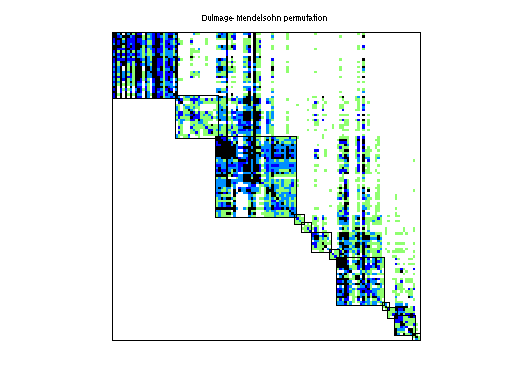Matrix properties
number of rows	364
number of columns	364
nonzeros	13,585
structural full rank?	yes
structural rank	364
# of blocks from dmperm	12
# strongly connected comp.	12
explicit zero entries	0
nonzero pattern symmetry	42%
numeric value symmetry	28%
type	integer
structure	unsymmetric
Cholesky candidate?	no
positive definite?	no

author	M. Monagan
editor	J.-G. Dumas
date	2008
kind	combinatorial problem
2D/3D problem?	no

Notes:

CAG matrix set from Michael Monagan, Simon Fraser Univ., Canada        
From Jean-Guillaume Dumas' Sparse Integer Matrix Collection,           
http://ljk.imag.fr/membres/Jean-Guillaume.Dumas/simc.html              
                                                                       
Strongly Connected Graph Components and Computing                      
Characteristic Polynomials of Integer Matrices in Maple,               
Simon Lo, Michael Monagan, Allan Wittkopf                              
{sclo,mmonagan,wittkopf} at cecm.sfu.ca                                
Centre for Experimental and Constructive Mathematics,                  
Department of Mathematics, Simon Fraser University,                    
Burnaby, B.C., V5A 1S6, Canada.                                        
                                                                       
abstract:                                                              
Let A be an n x n matrix of integers. We present details of our Maple  
implementation of a simple modular method for computing the            
characteristic polynomial of A.  We consider several different         
representations for the computation modulo primes, in particular, the  
use of double precision floats.  The algorithm used in Maple releases  
7-10 is the Berkowitz algorithm. We present some timings comparing the 
two algorithms on a sequence of matrices arising from an application in
combinatorics of Jocelyn Quaintance. These matrices have a hidden block
structure. Once identified, we can further reduce the computing time   
dramatically.  This work has been incorporated into Maple 11's         
LinearAlgebra package.                                                 
                                                                       
http://www.cecm.sfu.ca/~monaganm/papers/CP8.pdf                        
                                                                       
Filename in JGD collection: CAG/mat364.sms                             

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	16,233
Cholesky flop count	9.0e+05
nnz(L+U), no partial pivoting, with AMD	32,102
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	14,306
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	21,885

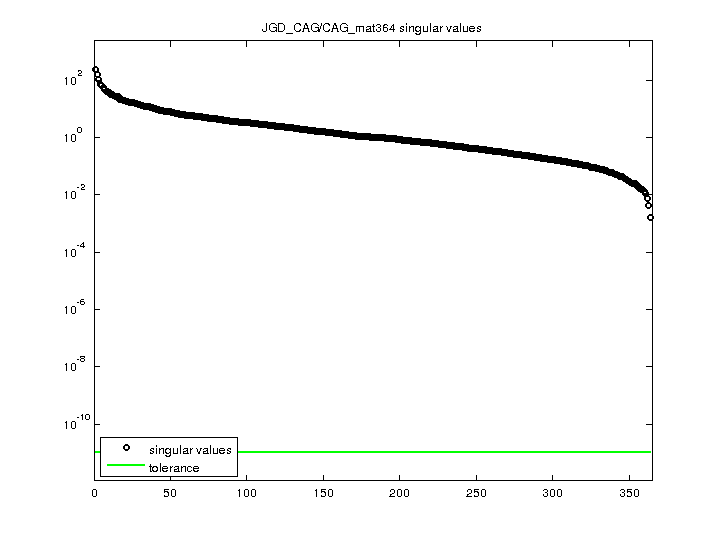
SVD-based statistics:
norm(A)	235.842
min(svd(A))	0.00164171
cond(A)	143656
rank(A)	364
sprank(A)-rank(A)	0
null space dimension	0
full numerical rank?	yes

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.