Matrix properties
number of rows	2,880
number of columns	2,880
nonzeros	18,229
structural full rank?	yes
structural rank	2,880
# of blocks from dmperm	177
# strongly connected comp.	107
explicit zero entries	1,406
nonzero pattern symmetry	7%
numeric value symmetry	0%
type	real
structure	unsymmetric
Cholesky candidate?	no
positive definite?	no

author	P. Hollinger
editor	T. Davis
date	2001
kind	economic problem
2D/3D problem?	no

Additional fields	size and type
b	full 2880-by-1
x	full 2880-by-1

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	157,432
Cholesky flop count	3.2e+07
nnz(L+U), no partial pivoting, with AMD	311,984
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	155,210
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	278,820

Note that all matrix statistics (except nonzero pattern symmetry) exclude the 1406 explicit zero entries.

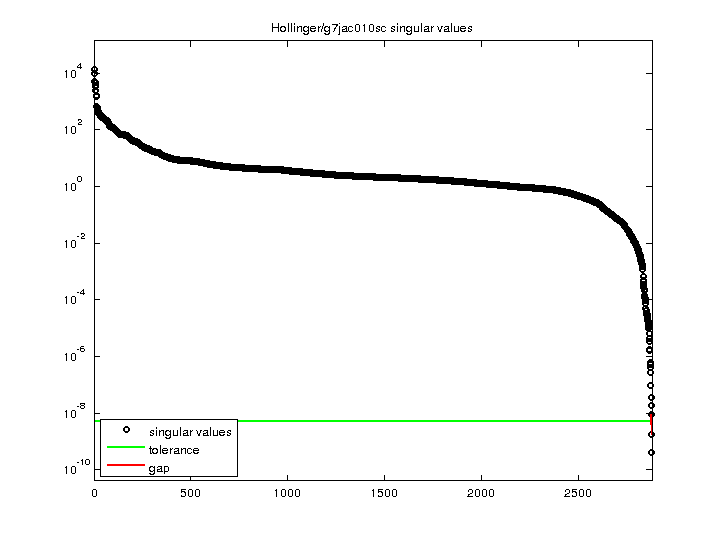
SVD-based statistics:
norm(A)	13934.5
min(svd(A))	3.97831e-10
cond(A)	3.50262e+13
rank(A)	2,878
sprank(A)-rank(A)	2
null space dimension	2
full numerical rank?	no
singular value gap	5.32371

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.