
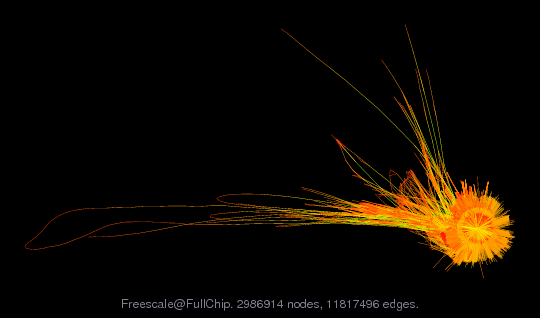
Matrix: Freescale/FullChip
Description: circuit simulation, Kiran Gullapalli, Freescale Semiconductor, Inc.
 |
 |
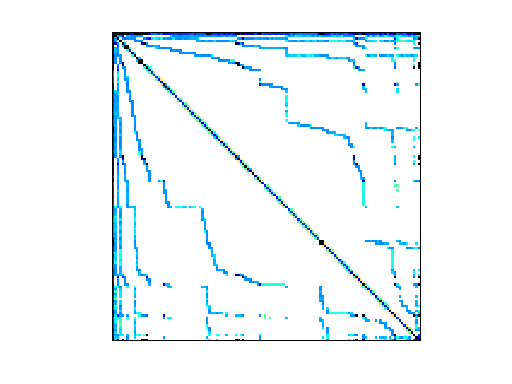
| (bipartite graph drawing) | (graph drawing of A+A') |
 |
 |
 |
| Matrix properties | |
| number of rows | 2,987,012 |
| number of columns | 2,987,012 |
| nonzeros | 26,621,983 |
| structural full rank? | yes |
| structural rank | 2,987,012 |
| # of blocks from dmperm | 35 |
| # strongly connected comp. | 35 |
| explicit zero entries | 7 |
| nonzero pattern symmetry | 100% |
| numeric value symmetry | 1% |
| type | real |
| structure | unsymmetric |
| Cholesky candidate? | no |
| positive definite? | no |
| author | K. Gullapalli |
| editor | T. Davis |
| date | 2011 |
| kind | circuit simulation problem |
| 2D/3D problem? | no |
Notes:
Full-chip circuit simulation matrix from Kiran Gullapalli, Freescale
Semiconductor, Inc.
This is a full-chip (everything that is actually built in silicon is
in the netlist), for an automotive part. For simulation, the
flash-memory and sram-memory cores are removed. But everything else is
in the matrix.
The chip takes an external battery (voltage source), but has internal
voltage generators. the node of the external battery can be removed
from the matrix. but the internal generators create some VERY HIGH
degree nodes. So, there are about 6 nodes with degree greater than
1000 (actually, the degree is 2M+ for 2 of these).
After ordering, nnz(L+U) = 200,180,468, with about 1.03793E+11
flops (a += b * c is counted as one flop).
| Ordering statistics: | result |
| nnz(chol(P*(A+A'+s*I)*P')) with AMD | 231,950,650 |
| Cholesky flop count | 1.0e+12 |
| nnz(L+U), no partial pivoting, with AMD | 460,914,288 |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 1925080767262 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 4412417792620 |
Note that all matrix statistics (except nonzero pattern symmetry) exclude the 7 explicit zero entries.
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.