Matrix properties
number of rows	29,282
number of columns	29,282
nonzeros	406,084
structural full rank?	yes
structural rank	29,282
# of blocks from dmperm	1
# strongly connected comp.	1
explicit zero entries	0
nonzero pattern symmetry	symmetric
numeric value symmetry	0%
type	complex
structure	unsymmetric
Cholesky candidate?	no
positive definite?	no

author	H. Dehghani
editor	T. Davis
date	2007
kind	electromagnetics problem
2D/3D problem?	yes

Additional fields	size and type
b	sparse 29282-by-1
Q	sparse 14641-by-1
nodes	full 14641-by-3
elements	full 28800-by-3

Notes:

% The problem is solving the fluence (PHI) of light in soft tissue using
% a simplified 3rd spherical harmonic expansion (SPN3) of the Radiative 
% Transport Equation.  There are two coupled equations to solve:        
% M1*phi1 = Q + (M2*phi2)                                   eq(1)       
% (M4 - (M3*inv(M1)*M2))*phi2 = -2/3*Q + M3*inv(M1)*Q       eq(2)       
% PHI = phi1 - (1/3).*phi2                                  eq(3)       
                                                                        
Problem = UFget ('Dehghani/light_in_tissue') ;                          
A = Problem.A ;                   % get the problem                     
Q = Problem.aux.Q ;                                                     
k = size (A,1) / 2 ;                                                    
M1 = A (1:k,1:k) ;                                                      
M2 = A (1:k,k+1:end) ;                                                  
M3 = A (k+1:end, 1:k) ;                                                 
M4 = A (k+1:end, k+1:end) ;                                             
elements = Problem.aux.elements ;                                       
nodes = Problem.aux.nodes ;                                             
                                                                        
Q2 = (-(2/3).*Q) + (M3*(M1\Q)) ;  % create rhs for equation 2           
Q2 = [sparse(k,1) ; Q2] ;                                               
phi2 = A\Q2 ;                     % solve for phi2                      
phi2 = phi2 (end/2+1:end,:) ;                                           
Q1 = Q + M2*phi2 ;                % calculate rhs for equation 1        
phi1 = M1\Q1;                     % solve for phi1                      
PHI = phi1 - (1/3).*phi2;                                               
figure (1) ; clf                  % plot results                        
trisurf(elements, nodes(:,1), nodes(:,2), nodes(:,3), log(abs(PHI))) ;  
shading interp ;                                                        
view (2) ;                                                              
colorbar('horiz') ;                                                     
axis equal ;                                                            
axis off ;                                                              
colormap hot ;                                                          

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	1,390,043
Cholesky flop count	2.0e+08
nnz(L+U), no partial pivoting, with AMD	2,750,804
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	2,925,391
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	5,672,099

SVD-based statistics:
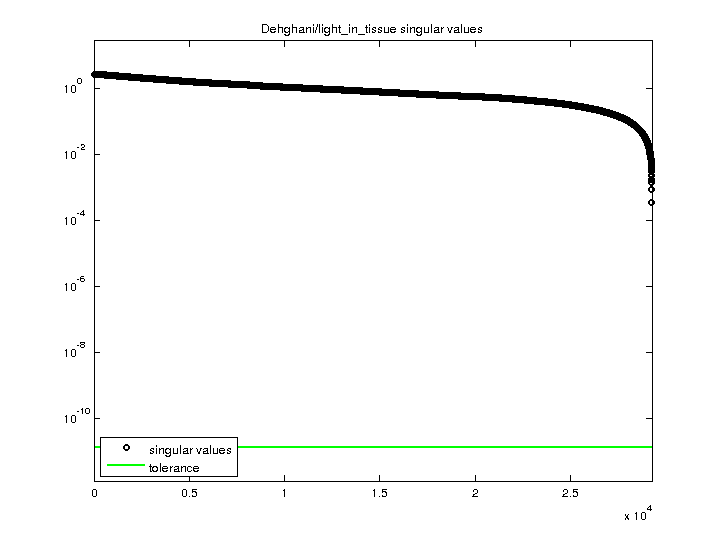
norm(A)	2.66355
min(svd(A))	0.000340525
cond(A)	7821.9
rank(A)	29,282
sprank(A)-rank(A)	0
null space dimension	0
full numerical rank?	yes

singular values (MAT file):	click here
SVD method used:	s = svd (full (A))
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.