Matrix properties
number of rows	11,077
number of columns	262,144
nonzeros	1,503,732
structural full rank?	yes
structural rank	11,077
# of blocks from dmperm	5
# strongly connected comp.	1
explicit zero entries	0
nonzero pattern symmetry	0%
numeric value symmetry	0%
type	integer
structure	rectangular
Cholesky candidate?	no
positive definite?	no

author	J. Dattorro
editor	T. Davis
date	2011
kind	optimization problem
2D/3D problem?	no

Additional fields	size and type
b	sparse 11077-by-1

Notes:

Dattorro Convex Optimization of Eternity II, Jon Dattoro           
                                                                   
An Eternity II puzzle (http://www.eternityii.com/) problem         
formulation A*x=b is discussed thoroughly in section 4.6.0.0.15 of 
the book Convex Optimization & Euclidean Distance Geometry which   
is freely available. That A matrix is obtained by presolving a     
sparse 864,593-by-1,048,576 system.  The 3 problems in this set    
contains three successive reductions, each equivalent to that      
larger system:                                                     
                                                                   
   * EternityII_E: a 11077-by-262144 system E*x=tau, where tau is  
       11077-by-1.  This is the million column Eternity II matrix  
       having redundant rows and columns removed analytically.     
       In the UF Collection, E is the Problem.A matrix, and tau    
       is Problem.b.  All entries in E are from the set {-1,0,1,2}.
       tau is binary and very sparse.                              
                                                                   
   * EternityII_Etilde: a 10054-by-204304 system Etilde*x=tautilde 
       with tautilde of size 10054-by-1.  The system has columns   
       removed corresponding to some known zero variables          
       (removal produced dependent rows).  In the UF Collection,   
       Etilde is the Problem.A matrix, and tautilde is Problem.b.  
       All entries in Etilde are from the set {-1,0,1}.            
       tautilde is binary and very sparse.                         
                                                                   
   * EternityII_A: a 7362-by-150638 system A*x=b, where b is       
       7362-by-1.  This system has columns removed not in          
       smallest face (containing tautilde) of polyhedral cone K =  
       { Etilde*x | x >= 0 }.                                      
                                                                   
The following linear program is a very difficult problem that      
remains unsolved:                                                  
                                                                   
    maximize_x z'*x, subject to A*x=b and x >= 0                   
                                                                   
The matrix A in the EternityII_A problem is sparse, having only    
782,087 nonzeros.  All entries of A are integers from the set      
{-1,0,1}.  The vector b is binary, with only 358 nonzeros.         
                                                                   
Direction vector z is determined by Convex Iteration:              
                                                                   
    maximize_z z'*x^{star},                                        
    subject to 0 <= z <= 1 and z'*1 = 256                          
                                                                   
(for a vector x, x >= 0 means all(x>-0) in MATLAB notation)        
                                                                   
These two problems are iterated to find a minimal cardinality      
solution x.  Constraint A*x=b bounds the variable from above by 1. 
Any minimal cardinality solution is binary and solves the Eternity 
II puzzle. The Eternity II puzzle is solved when                   
z^{star}'*x^{star} = 256.                                          
                                                                   
Minimal cardinality of this Eternity II problem is equal to number 
of puzzle pieces, 256.                                             
                                                                   
Comment: The technique, convex iteration, requires no modification 
(and works very well) when applied instead to mixed integer        
programming (MIP, not discussed in book). There is no modification 
to the linear program statement here except 256 variables,         
corresponding to the largest entries of iterate x^{star}, are      
declared binary.                                                   
                                                                   
For more details, see                                              
http://www.convexoptimization.com/wikimization/index.php           
/Dattorro_Convex_Optimization_of_Eternity_II (url is wrapped),     
and https://ccrma.stanford.edu/~dattorro/ .                        

Ordering statistics:	result
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	867,810,002
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	11,712,296

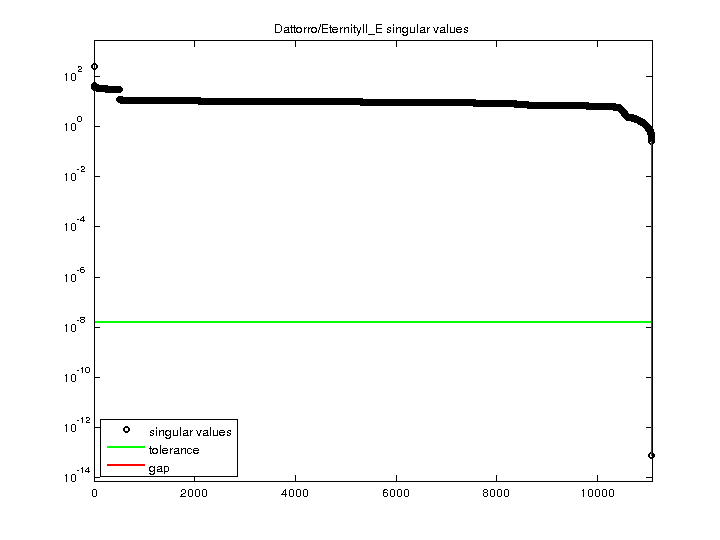
SVD-based statistics:
norm(A)	264.319
min(svd(A))	7.18761e-14
cond(A)	3.67743e+15
rank(A)	11,076
sprank(A)-rank(A)	1
null space dimension	1
full numerical rank?	no
singular value gap	3.43781e+12

singular values (MAT file):	click here
SVD method used:	s = svd (full (R)) ; where [~,R,E] = spqr (A') with droptol of zero
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.