Matrix: DIMACS10/cti
Description: DIMACS10 set: walshaw/cti
 |
| (undirected graph drawing) |
 |
| Matrix properties | |
| number of rows | 16,840 |
| number of columns | 16,840 |
| nonzeros | 96,464 |
| # strongly connected comp. | 1 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | symmetric |
| numeric value symmetry | symmetric |
| type | binary |
| structure | symmetric |
| Cholesky candidate? | no |
| positive definite? | no |
| author | C. Walshaw |
| editor | C. Walshaw |
| date | 2000 |
| kind | undirected graph |
| 2D/3D problem? | no |
Notes:
10th DIMACS Implementation Challenge:
http://www.cc.gatech.edu/dimacs10/index.shtml
As stated on their main website (
http://dimacs.rutgers.edu/Challenges/ ), the "DIMACS Implementation
Challenges address questions of determining realistic algorithm
performance where worst case analysis is overly pessimistic and
probabilistic models are too unrealistic: experimentation can provide
guides to realistic algorithm performance where analysis fails."
For the 10th DIMACS Implementation Challenge, the two related
problems of graph partitioning and graph clustering were chosen.
Graph partitioning and graph clustering are among the aforementioned
questions or problem areas where theoretical and practical results
deviate significantly from each other, so that experimental outcomes
are of particular interest.
Problem Motivation
Graph partitioning and graph clustering are ubiquitous subtasks in
many application areas. Generally speaking, both techniques aim at
the identification of vertex subsets with many internal and few
external edges. To name only a few, problems addressed by graph
partitioning and graph clustering algorithms are:
* What are the communities within an (online) social network?
* How do I speed up a numerical simulation by mapping it
efficiently onto a parallel computer?
* How must components be organized on a computer chip such that
they can communicate efficiently with each other?
* What are the segments of a digital image?
* Which functions are certain genes (most likely) responsible
for?
Challenge Goals
* One goal of this Challenge is to create a reproducible picture
of the state-of-the-art in the area of graph partitioning
(GP) and graph clustering (GC) algorithms. To this end we
are identifying a standard set of benchmark instances and
generators.
* Moreover, after initiating a discussion with the community, we
would like to establish the most appropriate problem
formulations and objective functions for a variety of
applications.
* Another goal is to enable current researchers to compare their
codes with each other, in hopes of identifying the most
effective algorithmic innovations that have been proposed.
* The final goal is to publish proceedings containing results
presented at the Challenge workshop, and a book containing
the best of the proceedings papers.
Problems Addressed
The precise problem formulations need to be established in the course
of the Challenge. The descriptions below serve as a starting point.
* Graph partitioning:
The most common formulation of the graph partitioning problem
for an undirected graph G = (V,E) asks for a division of V into
k pairwise disjoint subsets (partitions) such that all
partitions are of approximately equal size and the edge-cut,
i.e., the total number of edges having their incident nodes in
different subdomains, is minimized. The problem is known to be
NP-hard.
* Graph clustering:
Clustering is an important tool for investigating the
structural properties of data. Generally speaking, clustering
refers to the grouping of objects such that objects in the same
cluster are more similar to each other than to objects of
different clusters. The similarity measure depends on the
underlying application. Clustering graphs usually refers to the
identification of vertex subsets (clusters) that have
significantly more internal edges (to vertices of the same
cluster) than external ones (to vertices of another cluster).
There are 10 data sets in the DIMACS10 collection:
Kronecker: synthetic graphs from the Graph500 benchmark
dyn-frames: frames from a 2D dynamic simulation
Delaunay: Delaunay triangulations of random points in the plane
coauthor: citation and co-author networks
streets: real-world street networks
Walshaw: Chris Walshaw's graph partitioning archive
matrix: graphs from the UF collection (not added here)
random: random geometric graphs (random points in the unit square)
clustering: real-world graphs commonly used as benchmarks
numerical: graphs from numerical simulation
Some of the graphs already exist in the UF Collection. In some cases,
the original graph is unsymmetric, with values, whereas the DIMACS
graph is the symmetrized pattern of A+A'. Rather than add duplicate
patterns to the UF Collection, a MATLAB script is provided at
http://www.cise.ufl.edu/research/sparse/dimacs10 which downloads
each matrix from the UF Collection via UFget, and then performs whatever
operation is required to convert the matrix to the DIMACS graph problem.
Also posted at that page is a MATLAB code (metis_graph) for reading the
DIMACS *.graph files into MATLAB.
Walshaw: Chris Walshaw's graph partitioning archive
Chris Walshaw's graph partitioning archive contains 34 graphs that
have been very popular as benchmarks for graph partitioning algorithms
( http://staffweb.cms.gre.ac.uk/~wc06/partition/ ).
17 of them are already in the UF Collection. Only the 17 new graphs
not yet in the collection are added here in the DIMACS10 set.
DIMACS10 graph: new? UF matrix:
--------------- ---- -------------
walshaw/144 * DIMACS10/144
walshaw/3elt AG-Monien/3elt
walshaw/4elt Pothen/barth5
walshaw/598a * DIMACS10/598a
walshaw/add20 Hamm/add20
walshaw/add32 Hamm/add32
walshaw/auto * DIMACS10/auto
walshaw/bcsstk29 HB/bcsstk29
walshaw/bcsstk30 HB/bcsstk30
walshaw/bcsstk31 HB/bcsstk31
walshaw/bcsstk32 HB/bcsstk32
walshaw/bcsstk33 HB/bcsstk33
walshaw/brack2 AG-Monien/brack2
walshaw/crack AG-Monient/crack
walshaw/cs4 * DIMACS10/cs4
walshaw/cti * DIMACS10/cti
walshaw/data * DIMACS10/data
walshaw/fe_4elt2 * DIMACS10/fe_4elt2
walshaw/fe_body * DIMACS10/fe_body
walshaw/fe_ocean * DIMACS10/fe_ocean
walshaw/fe_pwt Pothen/pwt
walshaw/fe_rotor * DIMACS10/fe_rotor
walshaw/fe_sphere * DIMACS10/fe_sphere
walshaw/fe_tooth * DIMACS10/fe_tooth
walshaw/finan512 Mulvey/finan512
walshaw/m14b * DIMACS10/m14b
walshaw/memplus Hamm/memplus
walshaw/t60k * DIMACS10/t60k
walshaw/uk * DIMACS10/uk
walshaw/vibrobox Cote/vibrobox
walshaw/wave AG-Monien/wave
walshaw/whitaker3 AG-Monien/whitaker3
walshaw/wing * DIMACS10/wing
walshaw/wing_nodal * DIMACS10/wing_nodal
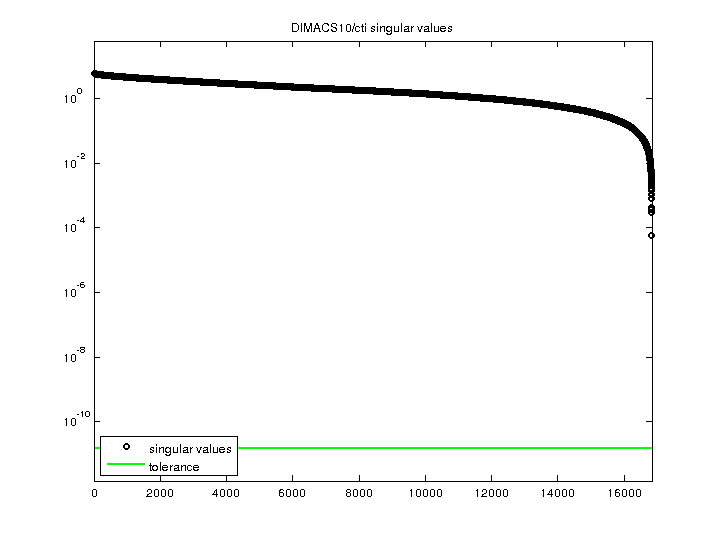
| SVD-based statistics: | |
| norm(A) | 5.96769 |
| min(svd(A)) | 5.82684e-05 |
| cond(A) | 102417 |
| rank(A) | 16,840 |
| null space dimension | 0 |
| full numerical rank? | yes |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (A)) ; |
| status: | ok |
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.