Matrix properties
number of rows	5,357
number of columns	5,357
nonzeros	207,123
structural full rank?	yes
structural rank	5,357
# of blocks from dmperm	1
# strongly connected comp.	1
explicit zero entries	572
nonzero pattern symmetry	symmetric
numeric value symmetry	symmetric
type	real
structure	symmetric
Cholesky candidate?	yes
positive definite?	yes

author	R. Kouhia
editor	R. Boisvert, R. Pozo, K. Remington, B. Miller, R. Lipman, R. Barrett, J. Dongarra
date	1997
kind	structural problem
2D/3D problem?	yes

Additional fields	size and type
coord	full 5357-by-3

Notes:

%                                                                              
%FILE  s3rmt3m3.mtx                                                            
%TITLE Cyl shell R/t=1000 grad trian mesh 1666 stab MITC3 elem with drill rot  
%KEY   s3rmt3m3                                                                
%                                                                              
%                                                                              
%CONTRIBUTOR Reijo Kouhia (reijo.kouhia@hut.fi)                                
%                                                                              
%BEGIN DESCRIPTION                                                             
% Matrix from a static analysis of a cylindrical shell                         
% Radius to thickness ratio R/t = 1000                                         
% Length to radius ratio    R/L = 1                                            
% One octant discretized with graded triangular mesh (1666 elements)           
% element:                                                                     
% facet-type shell element where the bending part is formulated                
% using the stabilized MITC theory (stabilization paramater 0.4)               
% the membrane part includes drilling rotations using                          
% the Hughes-Brezzi formulation with (regularizing parameter = G/1000,         
% where G is the shear modulus)                                                
% full 3-point integration                                                     
% --------------------------------------------------------------------------   
% Note:                                                                        
% The sparsity pattern of the matrix is determined from the element            
% connectivity data assuming that the element matrix is full.                  
% Since this case the  material model is linear isotropically elastic          
% there exist some zeros.                                                      
% Since the removal of those zero elements is trivial                          
% but the reconstruction of the current sparsity                               
% pattern is impossible from the sparsified structure without any further      
% knowledge of the element connectivity, the zeros are retained in this file.  
% ---------------------------------------------------------------------------  
%END DESCRIPTION                                                               
%                                                                              
%                                                                              

Ordering statistics:	result
nnz(chol(P*(A+A'+s*I)*P')) with AMD	438,361
Cholesky flop count	5.7e+07
nnz(L+U), no partial pivoting, with AMD	871,365
nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD	566,229
nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD	1,115,039

Note that all matrix statistics (except nonzero pattern symmetry) exclude the 572 explicit zero entries.

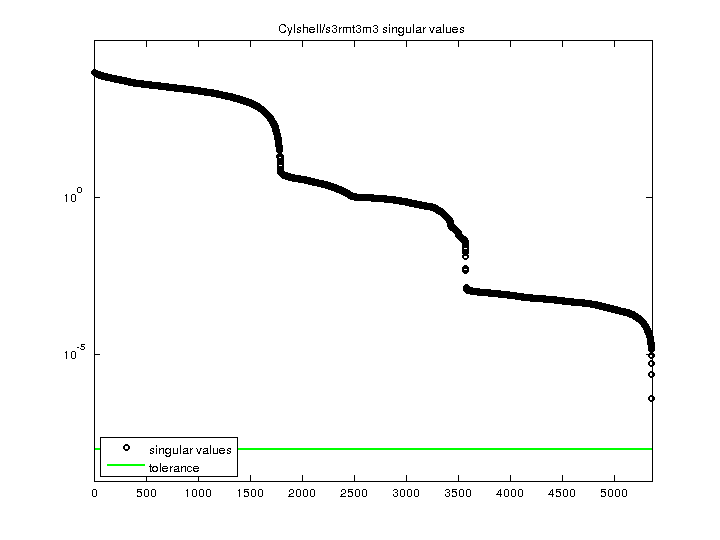
SVD-based statistics:
norm(A)	9598.61
min(svd(A))	3.99835e-07
cond(A)	2.40064e+10
rank(A)	5,357
sprank(A)-rank(A)	0
null space dimension	0
full numerical rank?	yes

singular values (MAT file):	click here
SVD method used:	s = svd (full (A)) ;
status:	ok

For a description of the statistics displayed above, click here.

Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.