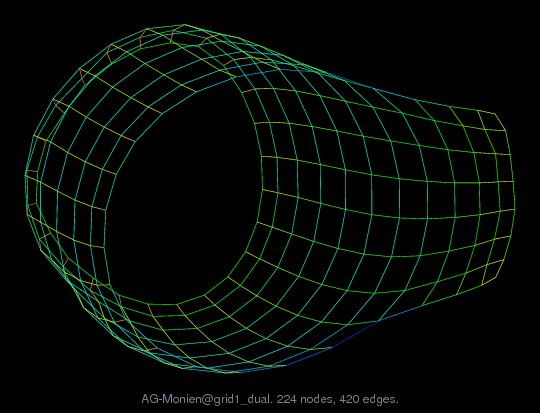
Matrix: AG-Monien/grid1_dual
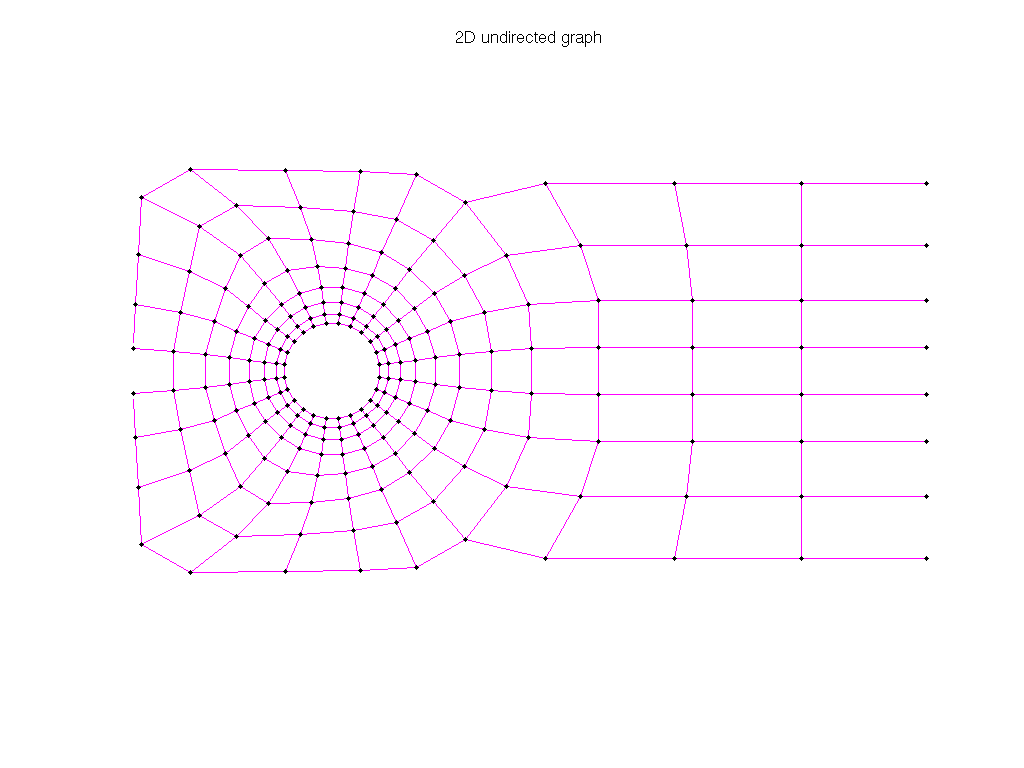
Description: 2D finite element problem
 |
| (undirected graph drawing) |
 |
 |
 |
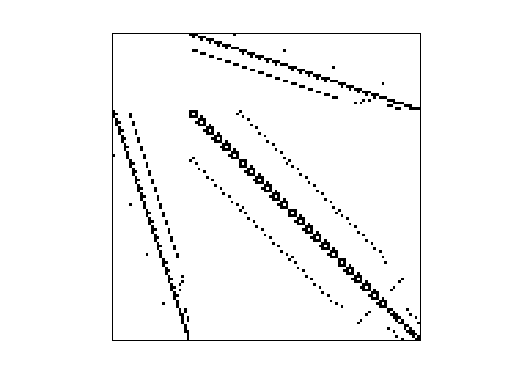
| Matrix properties | |
| number of rows | 224 |
| number of columns | 224 |
| nonzeros | 840 |
| structural full rank? | yes |
| structural rank | 224 |
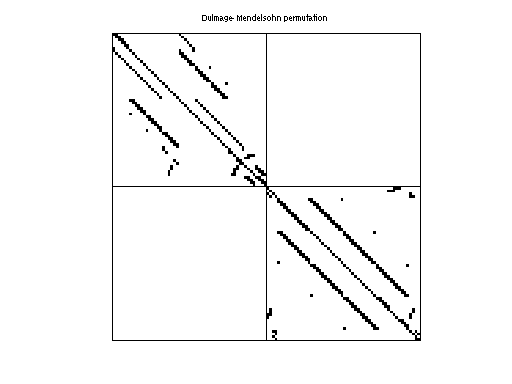
| # of blocks from dmperm | 2 |
| # strongly connected comp. | 1 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | symmetric |
| numeric value symmetry | symmetric |
| type | binary |
| structure | symmetric |
| Cholesky candidate? | no |
| positive definite? | no |
| author | R. Diekmann, R. Preis |
| editor | R. Diekmann, R. Preis |
| date | 1998 |
| kind | 2D/3D problem |
| 2D/3D problem? | yes |
| Additional fields | size and type |
| coord | full 224-by-2 |
Notes:
AG-Monien Graph Collection, Ralf Diekmann and Robert Preis
http://www2.cs.uni-paderborn.de/fachbereich/AG/monien/RESEARCH/PART/graphs.html
A collection of test graphs from various sources. Many of the graphs
include XY or XYZ coordinates. This set also includes some graphs from
the Harwell-Boeing collection, the NASA matrices, and some random matrices
which are not included here in the AG-Monien/ group of the UF Collection.
In addition, two graphs already appear in other groups:
AG-Monien/big : same as Nasa/barth5, Pothen/barth5 (not included here)
AG-Monien/cage_3_11 : same as Pajek/GD98_c (included here)
The AG-Monien/GRID subset is not included. It contains square grids that
are already well-represented in the UF Collection.
Six of the problem sets are included as sequences, each sequence being
a single problem instance in the UF Collection:
bfly: 10 butterfly graphs 3..12
cage: 45 cage graphs 3..12
cca: 10 cube-connected cycle graphs, no wrap
ccc: 10 cube-connected cycle graphs, with wrap
debr: 18 De Bruijn graphs
se: 13 shuffle-exchange graphs
Problem.aux.G{:} are the graphs in these 6 sequences. Problem.aux.Gname{:}
are the original names of each graph, and Problemm.aux.Gcoord{:} are the
xy or xyz coordinates of each node, if present.
| Ordering statistics: | result |
| nnz(chol(P*(A+A'+s*I)*P')) with AMD | 1,843 |
| Cholesky flop count | 2.1e+04 |
| nnz(L+U), no partial pivoting, with AMD | 3,462 |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 1,480 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 2,579 |
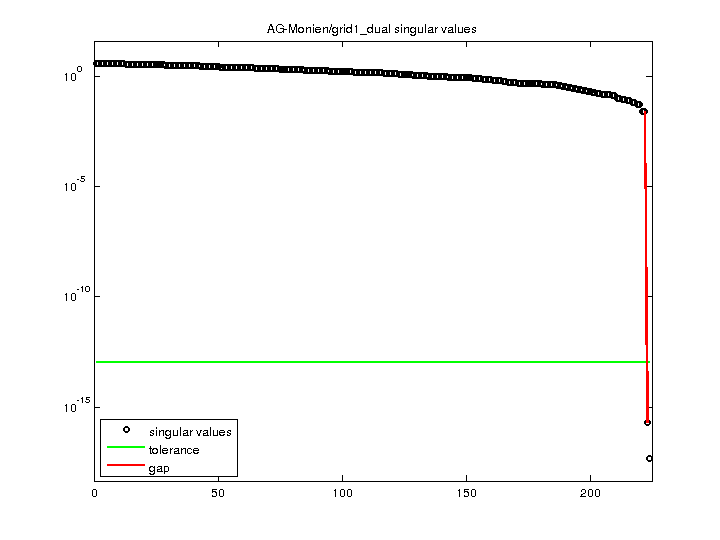
| SVD-based statistics: | |
| norm(A) | 3.89751 |
| min(svd(A)) | 4.44444e-18 |
| cond(A) | 8.7694e+17 |
| rank(A) | 222 |
| sprank(A)-rank(A) | 2 |
| null space dimension | 2 |
| full numerical rank? | no |
| singular value gap | 1.21785e+14 |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (A)) ; |
| status: | ok |
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.