



Next: Data Structures
Up: Algorithms
Previous: Plane Sweep Algorithm
This algorithm starts with constructing any triangulation. Then, the idea is to flip all non-locally Delaunay edges in this triangulation to be locally Delaunay. The concept of local Delaunayhood is discussed in [5] and [7]. A triangulation is Delaunay if and only if all edges are locally Delaunay. Algorithm uses a stack to keep all non-locally Delaunay edges. The stack contains at most one copy per edge and only the edges of the current triangulation. Following algorithm is due Charles Lawson and given in [5].
. Construct an arbitrary triangulation T of point set S.
. Push all non-locally interior edges of T on stack and mark them.
. While stack is non-empty do
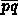 = pop()
= pop()
unmark 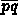
if 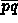 is non-locally Delaunay then
is non-locally Delaunay then
Replace 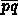 by the edge connecting the respective
by the edge connecting the respective
third vertices of the two incident triangles
Push other four edges of the two triangles into the stack if unmarked
Alper Ungor
Tue May 13 15:38:16 CDT 1997
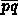 = pop()
= pop()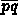
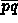 is non-locally Delaunay then
is non-locally Delaunay then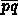 by the edge connecting the respective
by the edge connecting the respective