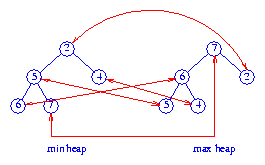
Figure 1 Dual heap
isEmpty() ... return true iff the DEPQ is empty
size() ... return the number of elements in the DEPQ
getMin() ...
return element with minimum priority
getMax() ...
return element with maximum priority
put(x) ...
insert the element x into the DEPQ
removeMin() ...
remove an element with minimum priority and return this element
removeMax() ...
remove an element with maximum priority and return this element
L,
M,
and
R.
The middle group
M contains a single element
called the pivot, all elements in the left group
L are <= the pivot, and
all elements in the right group
R are >= the pivot.
Following this partitioning, the left and right element groups
are sorted recursively.
M
is made as large as possible through the use of a DEPQ. The external
quick sort strategy is:
<= the smallest element in the DEPQ, output this
next element as part of the left group.
If the next element is
>= the largest element in the DEPQ, output this
next element as part of the right group.
Otherwise, remove either the max or min element from the DEPQ (the
choice may be made randomly or alternately); if the max element
is removed, output it as part of the right group; otherwise, output
the removed element as part of the left group; insert the newly input element
into the DEPQ.
remove(theNode) operation (this operation
removes the node theNode from the PQ).
The simplest of these methods, dual structure method,
maintains both a min PQ and a max PQ of all the DEPQ elements together
with correspondence pointers
between the nodes of the min PQ and the max PQ that contain
the same element.
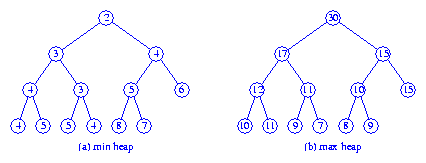
Figure 1 shows a dual heap structure for the elements 6, 7, 2,
5, 4. Correspondence pointers are shown as red arrows.

isEmpty and size operations are
implemented by using a variable size
that keeps track of the number of elements in the DEPQ. The minimum element is
at the root of the min heap and the maximum element is at the root of the
max heap. To insert an element x, we insert
x into both the
min and the max heaps and then set up correspondence pointers between
the locations of x in the min and max heaps. To remove the
minimum element, we do a removeMin from the min heap
and a remove(theNode), where theNode is the corresponding node for the removed element, from the max heap.
The maximum element is removed in an analogous way.
a
in the min PQ is
paired with a distinct element b of the max PQ.
(a,b) is a corresponding pair of elements such that
priority(a) <= priority(b).
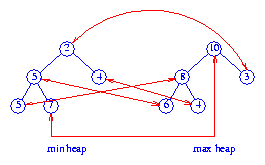
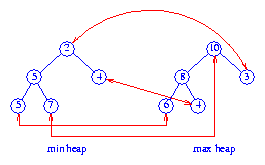
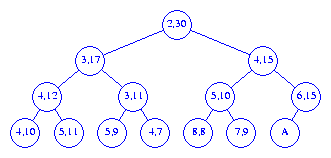
Figure 2 shows a total correspondence heap for the 11
elements 2, 3, 4, 4, 5, 5, 6, 7, 8, 9, 10. The element
9 is in the buffer. Corresponding pairs are
shown by red arrows.
put(x),
removeMin(),
and
removeMax() take O(log n) time
(n
is the number of elements in the DEPQ, for pairing heaps, this is an
amortized
complexity), and the remaining DEPQ operations take
O(1) time.
remove(theNode) operation,
we can, at times, obtain more elegant and more efficient
DEPQ structures using a custom strategy.
This, for example, is the case when adapting the heap structure.
For the heap structure, many adaptation strategies are possible.
These strategies have resulted in the DEPQ structures min-max heaps,
twin heaps, deaps, diamond deque, and interval heaps.
The simplest and most efficient of these is the interval heap.
P
be a and b, where
a <= b. We say that the node
P represents the closed interval
[a,b].
a is the left end point of the interval of
P, and b is its right end point.
The interval
[c,d] is contained in the interval
[a,b] iff
a <= c <= d <= b.
In an interval heap,
the intervals
represented by the left and right children (if they exist) of each node
P
are contained in the interval represented by P.
When the last node contains a single element with priority
c, then
a <= c <= b, where
[a,b] is the interval of the parent (if any)
of the last node.
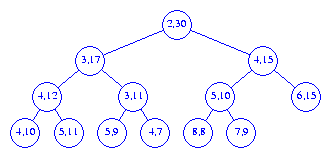
26
elements, only the element priorities are shown. You may verify that the
intervals represented by the children of any node P
are contained in the
interval of P.
n elements
is Theta(log n).
A
as is shown in Figure 6.
A
is [6,15]. Therefore, if the priority of the new
element is between 6 and 15,
the new element may be inserted into node A.
When the priority of the new element is less than the left end point
6 of the parent interval,
the new element is inserted into the min
heap embedded in the interval heap. This insertion is done using
the min heap
insertion procedure starting at node A.
When the priority of the new element is greater than the right end point
15 of the parent interval,
the new element is inserted into the max
heap embedded in the interval heap. This insertion is done using
the max heap
insertion procedure starting at node A.
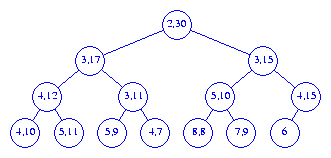
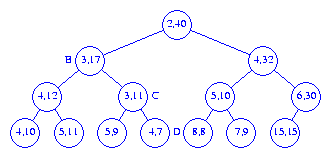
10
into the interval heap of Figure 4, this element is put into the node
A shown in Figure 6.
To insert an element with priority 3, we follow a path
from node A towards the root, moving left end points
down until we either pass the root or
reach a node whose left end point is <=
3. The new element is inserted into the node that now has no
left end point. Figure 7 shows the resulting interval heap.
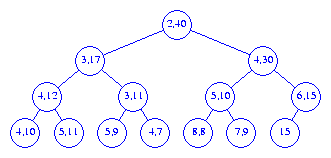
40 into the
interval heap of Figure 4, we follow a path
from node A (see Figure 6)
towards the root, moving right end points
down until we either pass the root or
reach a node whose right end point is >=
40. The new element is inserted into the node that now has no
right end point. Figure 8 shows the resulting interval heap.
A
denote the last node in the heap.
If the priority of the new element lies within the interval
[6,15] of the parent
of A, then the new element is inserted into
node A (the new element becomes the left
end point of
A if its priority is less than that of the
element currently in A).
If the priority of the new element is less than the left end point
6 of the parent
of A, then the new element is inserted into
the embedded min heap; otherwise, the new element is inserted into
the embedded max heap.
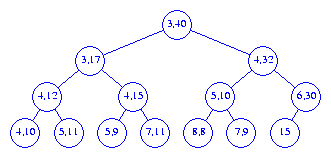
Figure 9 shows the result of inserting an element with priority
32 into the interval heap of Figure 8.
removeMin
operation fails.
p from
the last node. If this causes the last node to become empty, the last node
is no longer part of the heap. The point p
removed from the last node is
reinserted into the embedded min heap by beginning at the root. As we move
down, it may be necessary to swap the current p with the
right end point r
of the node being examined to ensure that
p <= r.
The reinsertion is done using the same strategy as used to reinsert into an
ordinary heap (see Program 13.3 of the text).
2 is removed
from the root. Next, the left end point 15 is removed
from the last node and we begin the reinsertion procedure at the root.
The smaller of the min heap elements that are the children of the root
is 3. Since this element is smaller than
15, we move the 3 into the root
(the 3 becomes the left end point of the root)
and position ourselves at the left child B
of the root. Since,
15 <= 17 we do not swap the right end point of
B with the current p = 15.
The smaller of the left end points of the children of B
is 3. The 3 is moved from
node C into node B as its
left end point and we position ourselves at node C.
Since p = 15 > 11, we swap the two and
15 becomes the right end point of node
C. The smaller of left end points
of Cs children is 4. Since
this is smaller than the current p = 11, it is moved into
node C as this node's left end point. We now position
ourselves at node D. First, we swap p
= 11 and Ds right end point. Now, since
D has no children, the current p =
7 is inserted into node D as
Ds left end point. Figure 10 shows the result.
removeMin operation, then reinsert the right end point
of this subtree's root using the strategy used for the
removeMax operation.
isEmpty(),
size(),
getMin(),
and
getMax() take O(1) time each;
put(x),
removeMin(),
and
removeMax() take O(log n) each;
and initializing an n element interval heap takes
O(n) time.
[a,b]?
For example, if the point collection is 3, 4, 5, 6,
8, 12, the points outside the range [5,7] are
3, 4, 8, 12.
O(log n) time,
where n is the number of points in the collection.
Note that given the location of an aribtrary element in an interval heap,
this element can be removed from the interval heap
in O(log n)
time using an algorithm similar to that used to remove an arbitrary
element from a heap (see Exercise 13.13 of the text).
Theta(k)
time, where k is the number of points outside
the range [a,b]. This is done using the following
recursive procedure:
return.
[a,b],
then all points are in the range (therefore, there are no points
to report), return.
[a,b].
[a,b].
[a,b].
return
[4,32]. We start at the root. Since the
root interval is not contained in the query interval, we reach step 3
of the procedure. Whenever step 3 is reached, we are assured that at least one
of the end points of the root interval is outside the
query interval. Therefore,
each time step 3 is reached, at least one point is reported. In our example,
both points 2 and 40
are outside the query interval and so are reported.
We then search the left and right subtrees of the root for additional points.
When the left subtree is searched, we again determine that the root
interval is not contained in the query interval. This time only one of the
root interval points (i.e., 3) is
to be outside the query range. This point is reported and we proceed
to search the left and right subtrees of B for
additional points outside the query range. Since the interval of the
left child of B is contained in the query range,
the left subtree of B contains no points
outside the query range. We do not explore the left subtree
of B
further. When the right subtree of B is searched,
we report the left end point 3
of node C and proceed to search the left and right
subtrees of C. Since the intervals of the
roots of each of these subtrees is contained in the query interval, these
subtrees are not explored further. Finally, we examine the root of the
right subtree of the overall tree root, that is the node with interval
[4,32]. Since this node's interval is contained
in the query interval, the right subtree of the overall tree is not
searched further.
Theta(number
of interval heap nodes visited). The nodes visited in the preceding
example are the root and its two children,
node B and its two children,
and node C and its two children.
Thus, 7 nodes are visited and a total of
4 points are reported.
3k + 1, where k
is the number of points reported. If a visited node reports one
or two points, give the node a count of one. If a visited node
reports no points,
give it a count of zero and add one to the count of its parent
(unless the node is the root and so has no parent). The number
of nodes with a nonzero count is at most k.
Since no node has a count more than 3,
the sum of the counts is at most 3k.
Accounting for the possibility that the root reports no point,
we see that the number of nodes visited is at most
3k+1. Therefore, the complexity of the
search is
Theta(k).
This complexity is asymptotically optimal because every algorithm that
reports k points must spend
at least Theta(1) time per reported point.
2
(1 because it is visited and reports at least one
point and another 1 because its right child is visited
but reports no point), node B gets a count of
2
(1 because it is visited and reports at least one
point and another 1 because its left child is visited
but reports no point), and node C gets a count of
3
(1 because it is visited and reports at least one
point and another 2 because its left and right children
are visited and neither
reports a point). The count for each of the remaining nodes in the interval
heap is 0.