Data Structures, Algorithms, & Applications in C++
Chapter 20, Exercise 1

(a)

The tree is obtained from Figure 20.2 by adding an additional level with 16 nodes. The edge labels for the new edges represent values of x4. The new tree is given below.

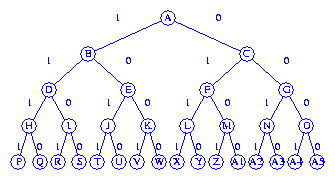
(b)

The backtracking algorithm starts at the root A and moves to B, D, H, and P. Since P is infeasible, no attempt is made to update the best solution found so far. We backup to H and then move to Q. Since Q is a feasible solution (the capacity used is 60 and the solution value is 114) and since it represents the best solution found so far, we record this fact. From Q, we backup to H and then to D. From D we move to I and then to R. R is an infeasible leaf and we backup to I and then move to S. S is a leaf with less value than the best found so far. We backup to I, then to D, and then to B. From B we move to E and examine all nodes in the order J, T, U, K, V, W. A better soltion is not found. From W, we backup to K, E, B, and A. The next move is to C. The remaining nodes in this subtree are reached in the order F, L, X, Y, M, Z, A1, G, N, A2, A3, O, A4, A5. Since no slution with value more than 114 is found, the solution described at node Q is the best.

The backtracking algorithm reaches all nodes in the tree. The order is: A, B, D, H, P, Q, I, R, S, E, J, T, U, K, V, W, C, F, L, X, Y, M, Z, A1, G, N, A2, A3, O, A4, A5.