Data Structures, Algorithms, & Applications in C++
Chapter 17, Exercise 39

(a)

Our greedy algorithm traverses the tree in postorder. During this traversal we compute, for each node x, the maximum delay, D(x), from x to any other node in its subtree. If D(x) exceeds d, the node x is deleted from T.

Consider the example tree shown below as tree (a) and assume d = 3.



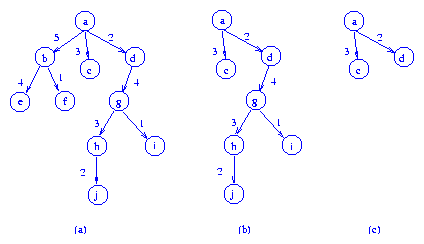
The delay, D(x), for x a leaf node is 0. So, D(x) = 0 when x is any one of the nodes {e, f, c, j, i}. In postorder, a node is visited after its children have been visited. When a node x is visited, its delay may be computed as:

D(x) = maxy is a child of x{D(y) + w(x,y)}

where w(x,y) is the weight/length of the edge (x,y). So, D(b) = 4 and D(h) = 2. Since D(b) > d = 3, we delete node b to get tree (b) of the above figure. Next, D(g) = 5 is computed and node g is deleted resulting in tree (c). D(d) = 0 and D(a) = 3. No more nodes are deleted. A high-level description of the greedy algorithm is given below. The algorithm assumes that S has been initialized to the empty set.

---

algorithm delete(t)
{// delete nodes within the subtree with root t and compute D(t)
   if (t != null)
   {
      // compute D(t)
      D(t) = 0;
      for (each child y of t)
      {
         delete(y);
         if (y is not in S)
            D(t) = max{D(t), D(y) + w(t,y)};
      }

      if (D(t) > d)
         // delete t
         add t to S;
   }
}

(b)

We may use induction to prove that the described greedy algorithm always finds a minimum cardinality set S such that the removal of the vertices in S from the tree T leaves behind a forest in which no root-to-leaf path has a length that is more than d.

The induction is on the number, n, of nodes in the tree T. If n = 0, the claim is trivially valid. Assume the claim is valid for n <= m where m is an arbitrary natural number. Let T be a tree with n + 1 nodes. Let S be the set of vertices deleted by our greedy algorithm, and let W be a minimum cardinality vertex set such that the removal of the vertices in W from the tree T results in a forest in which there is no root-to-leaf path whose length exceeds d. We need to show that |S| = |W|. If |S| = 0, this is trivially true. If |S| > 0, then let z be the first vertex added to S by our greedy algorithm. Let Tz be the subtree of T rooted at z. As z is added to S by our greedy algorithm, D(z) > d. Hence, W must contain at least one vertex u that is in Tz. If W contains more than one such u, then W cannot be of minimum cardinality as Z = W - {all such u} + {z} is such that the removal of the vertices in Z from the tree T leaves behind a forest in which there is no root-to-leaf path whose length exceeds d. Hence, W contains exactly one such u. Let W' = W - {u}. Let T' = T - Tz be the tree that results from the removal of Tz from T. If there is a W* such that |W*| < |W'| and the forst that results from removing the vertices in W* from T' has no root-to-leaf path whose length exceeds d, then since the forest that results when the vertices in W* + {z} are removed from T also has no root-to-leaf path whose length exceeds d, W is not a minimum cardinality deletion set for T. So, W' is a minimum cardinality vertex set. Also, S' = S - {z} is such that the rmoval of the vertices in S' from T' results in a forest in which there is no root-to-leaf path whose length exceeds d and furthermore S' is the answer produced by our greedy algorithm when started with T'. Since the number of vertices in T' is less than m + 1, |S'| = |W'|. Hence, |S| = |X'| + 1 = |W'| + 1 = |W|.

The complexity of our greedy algorithm is easily seen to be O(n) where n is the number of vertices in T.