GIS - Computational Problems: § 4: Advanced Problems
The majority of GIS datasets are
currently represented in vector format, and have an inherent
representational error that arises from sensor errors as well as from
discretization or polygonalization processes that we discussed in
detail in Section 2. GIS algorithms propagate this dataset error
through various stages of computation, yielding a GIS product or
result that often has unexpected errors. Such errors influence
coregistration (e.g., map overlay) and tend to corrupt the derivation
of range or elevation data from stereo imagery. This further impacts
the integration of surface models (e.g., spline models based on
elevation data) with GIS datasets.
Section Overview. In this section, we discuss errors in GIS
datasets as well as error and complexity measures, then investigate the
effect of such errors on elevation and surface modelling with GIS. The
section is structured as follows:
4.1. Estimating Error in GIS Datasets
4.2. Prediction of Error and Complexity in GIS Algorithms
4.3. Determining Elevation from Stereo Images in GIS Data
4.4. Integrating Surface Models with Elevation Data
In Section 4.1, we present an in-depth discussion of errors in
spatial datasets, together with measures for quantifying such errors
and various types of error analysis. Section 4.2 details techniques
for error analysis as well as the estimation of complexity in GIS
algorithms, both of which are required for the design and
implementation of accurate, efficient software. The difficult problem
of automatic analysis of stereophotogrammetric data is presented in
Section 4.3, and an extension of this problem to multi-modal GIS
(e.g., derived and measured elevation data) is discussed in Section
4.4.
Goals. For the purposes of the current course, goals for this
section include:
- Learning error/complexity analysis terminology and background;
- Exploring two error-related problems instantiated as
stereophotogrammetry and data integration
of vector- and image-format elevation data;
- Understanding the underlying issues of error detection,
measurement, modelling, and management in GIS; and
- Prediction of computational cost and accuracy (e.g., the
space-time-error bandwidth product) for a given GIS
algorithm.
We begin our discussion with a distinction between cartographic error
and GIS error.
4.1. Estimating Error in GIS Datasets
Note that map accuracy is a
relatively minor issue in cartography. Users of maps are rarely aware
of this problem, due to their familiarity with map notation and its
underlying assumptions. For example, if a map shows that a drainage
ditch runs parallel to a road, one assumes from world knowledge that
the ditch is located close to the road. However, on the map, for
purposes of cartographic license, the map may appear to be
offset laterally from the road by as much as the width of the
road.
4.1.1. Background.
In contrast to cartographic practice, GIS has evolved under the
following circumstances:
- GIS precision is limited only by computational hardware,
for example, ALU register size, cost of I/O and memory, or speed
of storage devices.
- All spatial data have limited accuracy which may be
expressed in terms of positional error, abstraction or generalization
error, measurement error, etc. Consider the following examples:
- Surveying error: Systematic or random errors in
measurement of distance or angle.
- Decision error: Vague geographic relations such
as west-of.
- Classification error: Soil type tends to occur
as a gradual transition in Nature but is characterized
by sharp between-class boundaries in GIS (e.g., sand,
loam, or silt).
- Stationarity error: Population density, land use
information, or income data not uniform over a given spatial
area over which the data is averaged.
- Relational error: Position and attribute error may
not be analytically related. For example, terrain elevation
is not necessarily a function of lateral position in
monocular satellite imagery, but is related to position in
binocular (stereoscopic) imaging.
- Precision of GIS processing exceeds data accuracy -- GIS
processing is performed at high (16- to 32-bit) arithmetic
precision, but GIS data have much lower precision (e.g., four to
ten parts per 10,000).
- In conventional map analysis, precision is usually adapted
to accuracy
- Precision limit of paper is approximately 0.5mm
or one linewidth, and map error increases with humidity
and use, due to paper warpage.
- Area accuracy is thus approximately m2.
- Map processes (planimetry, dot counting, transparency
overlay) have approximately the same error (one linewidth).
- The ability to change scale and combine data at different scales
implies that GIS precision is not necessarily adapted to
accuracy.
- Example. GIS systems generally do not warn
users if datasets of different scale (e.g., 1:24,000
vs. 1:1,000,000) are combined and the result is displayed
at 1:50,000 scale. This causes loss (aliasing) of
information from the high- (low-) resolution dataset.
- Observation. Most vector-based systems perform
vector operations (line intersection, overlay, area computation)
at full computational precision, without regard for dataset
accuracy. Users are often surprised by errors when GIS is
validated against ground truth.
- The accuracy of complex spatial objects is not well understood.
The accuracy of points, lines, and simple neighborhood areas (e.g.,
circle or rectangle) has been analyzed extensively. However,
methods of abstracting error as a function of lateral position
is not clear.
- The goal of GIS error analysis is a measure of uncertainty
associated with every GIS product (e.g., datasets, maps, and
analyses).
- Ideal: A set of confidence limits with each map.
- Problems: Cartographic license, map warpage and
digitization errors, other errors listed previously
can produce a diversity of error modes and magnitudes
in GIS datasets.
- Reality: Error measures are likely on points and
lines, maybe some for area, since supporting theory can
be derived rigorously from map coordinate information.
Hence, the key issues in this section are measurement,
estimation, and prediction of GIS error. The following
observations pertain:
- GIS attributes are often non-numeric and cannot (in some cases)
be indexed in a physically faithful way by a subset of the real numbers.
- The root problem in this case can be stated as follows:
- All physical science is defined in terms of mathematics, which
is based on measurement theory and the formal logic.
- In contrast, language and humanistic pursuits (from which
the process of classification arises) have as yet no
rigorous supporting or descriptive mathematics.
- Thus, attributes or labels, which are linguistic entities,
cannot in many instances be rigorously assigned numerical
values or ranked in a physically significant way.
4.1.2. Current Approaches to GIS Error Modelling.
The following discussion is adapted from Veregin (1994).
The error modelling process can be decomposed into the following steps
or levels:
Level 1. Error source and mode isolation -- Determine at
what locations in a given algorithm
errors arise, and in what form such errors occur.
Level 2. Error detection and measurement -- Devise and
implement test procedures for detecting and estimating
error deterministically or stochastically.
Level 3. Error propagation modelling -- Predict or estimate
the accrual of error as a computational cascade
comprised of a sequence of operations.
Level 4. Strategies for error management -- Determine methods
for carrying out GIS computations to achieve minimum
output error.
Level 5. Strategies for error "reduction" -- Note that the
common assumption is erroneous, namely, that error can
be reduced via summation over error distributions. In
practice, such distributions are often asymmetrical
with nonzero means. Indeed, the assumption that error
can be nontrivially reduced derives from convenient
pedagogic examples that employ symmetric distributions
with zero mean or assume infinite computational
precision. In practice, "error reduction" often
strives to re-order the processes of a GIS algorithm,
or substitute less erroneous processes, which is a type
of error management.
At Level 1 (error isolation), the following types of error are found:
- Positional, Locational, or Cartographic error,
which derive from map coordinate data;
- Thematic, Atrribute, or Descriptive error,
pertaining directly to GIS attributes;
- Measurement error, describing imprecision in cartographic
or thematic features;
- Conceptual error, which occurs when translating field data
into map objects (similar to Generalization error);
- Quantitative error respective to interval and ratio data
(on R); and
- Qualitative error respective to nominal or ordinal data
(indexed by N).
In this course, we will concentrate upon positional and attribute error
primarily, and thus examine Levels 1-5 of the preceding hierarchy for
error sources.
Level 1 (Error isolation) sources of error are classified by type
as shown in the following examples:
Positional: GPS and theodolite (surveying equipment) error,
or object location errors due to
misunderstanding of cartographic license.
Attribute: Poor assessment of attributes to due measurement,
conceptual, quantitative or qualitative error, as
well as systematic (e.g., operator) error in
manual classification systems.
Level 2 (Error detection and measurement) focuses on methods of
assessing accuracy levels in spatial data, for example:
- Digitization practices can be scrutinized to detect systematic
error or imprecision (e.g., a loose or misaligned piece of
mechanical equipment). Such problems can lead to positional,
measurement, and conceptual error.
- Similarly, spaceborne or airborne imaging platforms can
exhibit positional error due to vibration, measurement error
due to spectral filter response drift with time and
temperature, and conceptual error due to mis-classification of
terrain features by spectral signatures that are specified
erroneously a priori.
Level 3 (Error propagation modelling) focuses on error
propagation and error production, which are distinguished in the
following examples:
- Error Propagation always increases the error magnitude
at the output of an operation with respect to the error magnitude
at its input. Theory for estimating error propagation is well
known for linear systems, but is less well established for
nonlinear systems.
- Error Production (computational error) results
primarily from roundoff errors in arithmetic operations and
truncation of series approximations. An additional source of
computational error is the approximation of transcendental
functions by lookup tables.
Level 4 (Error management) focuses on coping with error and
making specifiably accurate decisions in the presence of error. In
GIS, this can involve:
- Specification of minimum accuracy standards for GIS
product acceptance, such as:
- Thematic- or attribute-specific standards
- Accuracy levels for cartographic feature specification
- Methods of inference derived from artificial
intelligence and information theory, especially concerning
decision in the presence of uncertainty.
Level 5 (Strategies for error reduction) includes but is not
limited to the following methods:
- Heuristics and decision trees for minimizing or
reducing error propagation, for example, placing more erroneous
operations at the end of a computational cascade, which can
involve out-of-order execution of instructions;
- Use of expert knowledge, replacement data, or checking
procedures, as follows:
- Expert Knowledge: For example, which input (e.g., a
given imaging sensor or spectral band of a multispectral
camera) to use when detecting a given object type, with the
goal of achieving high signal-to-noise ratio (SNR).
- Replacement Data: Use a lower-noise dataset for a
given high-error computation (although there may be tradeoffs
due to noise and resolution)
- Checking Procedures: Use fast, low-precision
operations until error accumulates to a prespecified
(estimated) level, then switch to slower, more precise
operations (e.g., using more terms in a series approximation
of a transcendental function).
4.1.3. Examples of Key GIS Errors.
The majority of GIS errors can be exemplified by the following three
case studies. In Section 4.1.3.1, we discuss polygon
fragmentation in map overlay. Section 4.1.3.2 contains an
overview of thematic and attribute errors, and Section 4.1.3.3
summarizes category-based error.
4.1.3.1. Case Study: Polygon Fragmentation Error.
Concept. Let there exist multiple maps ai,
where i = 1..n, which are defined on a two-dimensional domain
X. In practice, due to misalignments between map features in
each map, spurious polygons result from superimposing the polygon
boundaries of each ai.
Theory. Given ai 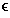 FX, where
1
FX, where
1  i
i
 n, let there be
ki polygons per layer. According to McAlpine and
Cook [McA71], an estimate of the number of spurious polygons
is given by:
n, let there be
ki polygons per layer. According to McAlpine and
Cook [McA71], an estimate of the number of spurious polygons
is given by:
kovl = (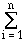 ki1/2 )2 .
ki1/2 )2 .
This process is illustrated in Figure 4.1.1. Note that kovl
rises exponentially with n, which means that spurious polygons tend to
shrink exponentially as n increases, due to the constant size
of X.
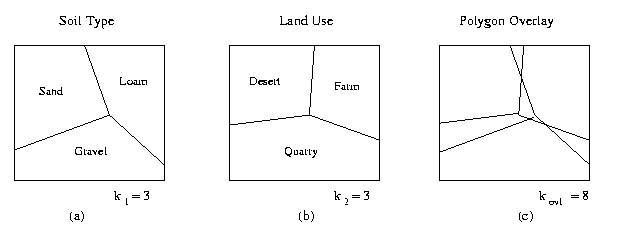
Figure 4.1.1. Effect of overlaying two maps (a,b) with polygons
to produce a map (c) with fragmented polygons.
Levels of Error Modelling (per Section 4.1.2):
1. Error Isolation: Polygon fragmentation is an example of
cartographic or positional error.
2. Error Detection could involve, for example, comparing
polygon size to a prespecified threshold (e.g., the IDRIS system's
MERGE command). However, in practice, this approach is
flawed by a lack of correlation between polygon size and
representational error.
3. Error Propagation: Models of polygon fragmentation are
typically based on ki, the number of polygons per layer,
rather than spatial error per layer or per polygon. Hence, analysis
must be modified such that another measure, such as polygon size, is
employed to characterize or detect error.
Goodchild [-] developed an error model based on the intersection of a
truthed cartographic line and its digitized representation in
different layers.
Given two layers with numbers of line vertices denoted by
v1 and v2, the maximum number of spurious
polygons is given by:
max(Np) = 2 · min(v1,v2)
- 4 .
If regular interleaving of vertices exists as shown in Figure 4.1.2,
then the number of spurious polygons is estimated by Goodchild as:
Np ~
2 v1 v2 / (v1 + v2) - 3 ,
which has been shown to be an overestimate [Ver94]. Additionally, the
relationship between the number of vertices and the number of spurious
polygons has been observed to vary considerably.

Figure 4.1.2. Two types of vertex interleaving in digitized datasets.
4.1.3.2. Case Study: Thematic and Attribute Error.
Attribute error requires a different modelling approach, since it may
not be rigorously mapped to an indexing set. For purposes of convenience,
we assume raster data.
Notation. Given n data layers, where each layer is defined on an
M×N-pixel domain X (i.e., there are |X| cells per data
layer), let aj(x) and
bj(x) denote truthed and estimated values
of the x-th cell in layer j.
Theory. Given layers 1  i,j
i,j
 n, the covariance for layers
i and j is given by:
n, the covariance for layers
i and j is given by:
sij = (1/|X|) ·
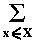 (aj(x) - bj(x))
(ai(x) - bi(x)) .
(aj(x) - bj(x))
(ai(x) - bi(x)) .
When i = j, this equation defines the error variance within a given
data layer.
Observation. The preceding equation facilitates calculation of
the error variance of a composite map a 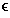 (Fn)X as a
function of a prespecified arithmetic operator applied during map
overlay.
(Fn)X as a
function of a prespecified arithmetic operator applied during map
overlay.
Example 1. When n layers are added, the composite error variance
is given by [Ver94]:
sc = 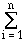
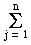 sij .
sij .
Remark. Although error variance is always positive per
layer, the error covariance may be positive or negative. Negative
error covariance can imply that the error variance of the composite
map may be lower than the variances of the indiviudal map layers.
This would appear to contradict the absolute error assumption,
namely, that absolute error of a map cannot be less than the error of
its most erroneous component map. However, this appearance is false,
since we are dealing with signed error, not the absolute value of an
error measure.
Example 2. When a subtraction operator is applied to n layers,
the composite error variance is given by [Ver94]:
sc = 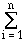
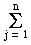 sij
- 4 ·
sij
- 4 ·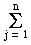 s1j .
s1j .
Implementational Issues. The preceding method depends upon one's
ability to measure variance and covariance for a given dataset. This
implies that a and b coincide spatially (i.e.,
are coregistered), which may not hold in practice for irregular polygons.
Note that rasterization can achieve some spatial alignment at the pixel
level, albeit at the cost of additional spatial and attribute error.
4.1.3.3. Case Study: Errors in Categorical Data.
Attributes that are classified taxonomically (i.e., categorized) may
be difficult to map to an index set in a rigorous manner. Hence,
one may want to deal with misclassification and erroneous assignment
in a probabilistic fashion.
Concept. Errors in GIS data layers can be modelled via a
contingency table approach.
Algorithm. Given attribute (e.g., cover) classes,
Step 1. Crosstabulate actual and estimated cover classes
for a selected cell sample.
Step 2. Calculate the fraction of cells correctly classified
for each layer.
Step 3. Determine map accuracy using inferential statistics,
per the following discussion.
Remark. A minor modification of this algorithm uses the same
number of samples from each cover class, to avoid error due to
under-representation by small sample size.
Example. Consider employment of the logical and operator
to match attributes between GIS data layers. Given the i-th layer with
fraction Pr[Ei] of cells correctly classified, the
composite map accuracy is given by:
Pr[Ec] = Pr[E1 and
E2] = Pr[E1] · Pr[E2 | E1] ,
where the conditional probability Pr[E2 | E1]
denotes the fraction of cells correctly classified in Layer 1 that
are correctly classified in Layer 2. For more than two layers,
the composite map accuracy is given by:
Pr[Ec] = Pr[E1
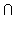 E2
E2
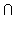 ...
...
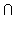 En]
= Pr[E1] · Pr[E2 | E1]
·
En]
= Pr[E1] · Pr[E2 | E1]
· 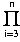 Pr[E1 |
Pr[E1 |
 (Ei)] ,
(Ei)] ,
where
 (Ei) =
(Ei) =
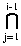 Ej .
Ej .
From these equations, minimum and maximum composite map accuracy can
be computed as:
Pr[Ecmax] = min(Pr[Ei]), i = 1..N
Pr[Ecmin] = max(0,
1 - 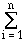 Pr[Ei]) ,
Pr[Ei]) ,
where Pr[Ei] denotes the fraction of cells in layer i that
are misclassified.
Observation. The preceding results yield several concepts and
observations concerning map accuracy and the logical and or
set-intersection operator, as follows:
- Composite map accuracy will at best equal the accuracy
of the least accurate layer. This occurs when misclassified cells
in each layer are coregistered with those in the least accurate
layer.
- At worst, composite map accuracy will be given by
1 -
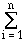 Pr[Ei] .
Pr[Ei] .
- Accuracy as a function of n can be represented by a negative
exponential curve.
The following related discussion of categorical coverages is taken
from [Chr94].
Recall. Coregistration and co-location in map overlay is a
fundamental operation upon which more complex GIS procedures are
constructed.
Observation. Map overlay employs positional information to
construct new polygons that share characteristics of the separate
source layers or primary maps. One can think of overlay as visually
implementing Venn diagrams applied to geographic database queries.
Figure 4.1.3 is illustrative of the inheritance problems that result
from misregistered data.

Figure 4.1.3. Map overlay can be
thought of as implementing Venn diagrams. Regions A  C and B
C and B  D inherit, or share
characteristics of, their components.
D inherit, or share
characteristics of, their components.
Definition. A categorical coverage is a type of GIS map
whose error model has spatial units that are adjusted on a continuous
space (i.e., a subset of Rn) to reflect categorical
distinctions.
Example. Categorical coverage is portrayed in Figure 4.1.4,
which shows a three-class soil labelling problem. Assume that the
labels are based on soil density (e.g., density(silt) >
density(loam) > density(sand)). Since density
measures can be expressed in terms of a subset of R, and the
density-based labelling problem exemplified in Figure 4.1.4 occurs on
the continuous domain R2, this is a categorical coverage
problem.
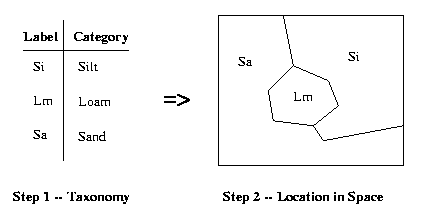
Figure 4.1.4. Example of categorical coverage problem,
a type
of map distinct from collection units.
Remark. In distinguishing categorical coverages from
more usual collection maps, the important consideration
is whether spatial attribute data take precedence.
Observations. The following instances are illustrative of some
differences between categorical coverage and collection zone maps:
- The term chloropleth maps previously referred to
geographic maps that had categorized attributes added later --
the places or locations in space existed, then
attributes were added. Presently, chloropleth refers to
categorical maps derived from classed continuous distributions
(e.g., the density example of Figure 4.1.4).
- In collection zones, spatial boundaries are usually
arbitrarily placed. In the past, autocorrelation was used to
reduce boundary artifacts (e.g., measurement errors).
Unfortunately, one must asume that some underlying classification
has been obscured by zone boundary errors. Error correction
involves a weight matrix that depicts relationships between
collection units.
Example. In sociological studies, the geographic unit may
be a city block or township, when in fact a person, firm, or
household would be more appropriate. This difference can be due
in part to the availability of statistical data over prespecified
spatial domains (e.g., census data organized geographically).
- In agronomic maps (e.g., soil surveys), similarlity or
consistency of attribute type often indicates that the map was
preceded by a taxonomic analysis. Positional accuracy, scale, and
cartographic license become more important than in the
collection zone case.
As part of this case study of errors in categorical data, we present
the following high-level discussion of the effects of category error
and overlay error in GIS maps.
Observation. The most common form of map overlay error is
called a sliver, as shown in Figure 4.1.5. Some GIS become
clogged with polygon representations of slivers and hence require
spatial filtration. An example of this is the MERGE
command in the IDRIS system.
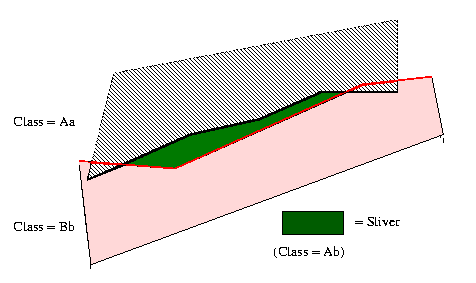
Figure 4.1.5. "Slivers", the most common map overlay error.
Remark. While slivers are caused by positional error, the
result is one or more classification errors (e.g., Ab in Figure
4.1.5). If the classes Aa and Bb are similar taxonomically, then Ab
can be resolved to Aa, assuming that A is the dominant feature or
attribute. In practice, this apparently obvious distinction can
become obscured due to the interdependence of positional and
classification errors.
Method. Existing techniques for analysis of categorical data
can be adapted to GIS, for example:
- General linear model [Bis75], [Bib77]
- Log-Linear model: linear in logarithms of
frequency-of-occurrence
- Logit/Probit model: linear in logarithms of ratios
Observation. The log-linear model allows a contingency table to
be decomposed into effects in terms of a hierarchical model. Salient
features of the log-linear model are listed as follows:
- The model is linear in logarithms because probabilities of
independent events combine multiplicatively, per Bayes' Law.
- If an analysis of variance (ANOVA) is applied, then the
following statements hold:
- The terms of the ANOVA include an error term for each case
or observation.
- The log-linear model only considers cells of the
contingency table (a good choice for categorical coverages,
due to lack of an independent case).
- Each table cell represents a Venn diagram combination due
to the map overlay process.
This concludes our brief discussion of category-based errors. We next
consider the error prediction and modelling process, which includes
sensitivity analysis.
4.2. Prediction of Error and Complexity in GIS Algorithms
In order to employ statistical methods
in analysis and prediction of GIS algorithm error, confidence limits
are required for each dataset. Such measures can be propagated through
error models, which can be designed to test algorithm sensitivity to a
variety of input perturbations. In Section 4.2.1, we discuss the
generation and interpretation of suitability maps, which can portray
the utility of a dataset in a given GIS processing scenario. Section
4.2.2 overviews the process of GIS sensitivity analysis, and Sections
4.2.3 and 4.2.4 discuss the use of specialized software to determine
error bounds on GIS algorithms. The analysis of complexity in GIS
algorithms is summarized in Section 4.2.5.
4.2.1. Suitability Map Generation
The following high-level model describes the process of suitability
map generation from primary maps that describe observed physical
reality (e.g., ground truth).
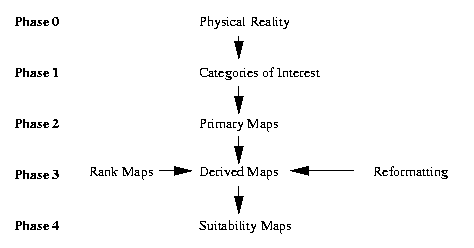
Figure 4.2.1.
Underlying model of suitability analysis applied to confidence limits.
Definition. A primary map is a map of an existing
geographic entity of interest (e.g., geologic or vegetation map).
Definition. A rank map has attributes that are ordinal-,
interval-, or ratio-valued and pertain to rankings that represent
mathematical relations between attributes of more than one map. For
example, a soil map could be ranked to determine potential for
landslides or rate of water percolation.
Definition. Geographic suitability analysis applies a
given operation or transformation to the attributes of one or more
maps, for example, a rank map or an overlay.
Notation. Given n primary maps that are overlaid, let salient
variables be defined as follows:
Definition. The result of a suitability analysis restricted to
the p-th polygon of the resultant suitability map has an attribute
rp that is a function of the weight vector w =
(w1, w2, ... , wn) and the attribute
vector ap = (ap1, ap2,
... ,apn)', as follows:
rp = f(w,ap) ,
which yields the resultant vector r = (r1,
r2, ... , rP(n)).
Observation. If ap is replaced by point or line
attributes (e.g., raster data is employed), then the preceding
formulation attains full generality, including most commonly known GIS
suitability analyses. In particular, the weighted intersection
overlay is represented by:
rp = f(w,ap) = 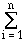 wi ·
ap,i , p = 1,2,...,P(n) .
wi ·
ap,i , p = 1,2,...,P(n) .
Observation. The multidimensional scaling approach derives
rp from the primary map attributes and a given attribute
ci, where i = 1..n, as follows:
rp = f(w,ap) = (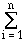 wi · ap,i)1/2 , p = 1,2,...,P(n) .
wi · ap,i)1/2 , p = 1,2,...,P(n) .
Note that the scalar ci is chosen for each of the primary
or rank maps. Hence, c = (c1, c2, ...,
cn).
Given the preceding theory, we now address the problem of sensitivity
analysis of GIS algorithms.
4.2.2. GIS Sensitivity Analysis
The difference between error propagation analysis (or error
analysis) and sensitivity analysis is as follows:
- Geographic sensitivity analysis perturbs the primary
maps to yield an output that is compared with the original map
obtained by combining unperturbed inputs in the same was as the
perturbed inputs were combined.
- Error propagation analysis uses error propagation theory to
analyze a GIS algorithm's effect on the output map, and may also
employ the aforemnetioned perturbation methods.
- In terms of the theory given in Section 4.2.1, sensitivity
analysis is more interested in the operation f and on the
effects upon f's output of perturbations in w and
ap.
Definition. Confidence limits for attribute errors
indicate the range of validity in an output attribute value given the
error ranges in the input attribute values (e.g., in the primary
maps).
Algorithm. The process of suitability map generation involves
the following steps:
Step 1. Given m primary maps, create n rank maps.
Note: If m < n, then more than one unique rank map must
be generated for a collection of primary maps. If m > n, then more
than one primary map yields one rank map. Hence, we assume m = n,
for convenience.
Step 2. Intersect the polygons of the n rank maps to yield
the P(n) polygons of the suitability map. Attribute values are
given by Equations (II) or (III).
Step 3. Transform primary map attributes to rank map
attributes (interval or ratiometric data that connote a ranking),
as follows:
Ti(bp,i) = ap,i , where i = 1..n,
p = 1..P(n) .
Step 4.Transform rank map attributes to suitability map
attributes via Equation (II) or (III).
Observation. One can represent the attributes of the
suitability map as
rp = 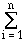 wi · ap,i =
wi · ap,i = 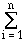 wi ·
Ti(bp,i) , p = 1,2,...,P(n) .
wi ·
Ti(bp,i) , p = 1,2,...,P(n) .
to obtain overlay suitability and
rp = (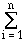 wi · (ap,i -
ci)2 )1/2 = (
wi · (ap,i -
ci)2 )1/2 = (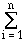 wi ·
(Ti(bp,i) -
ci)2 )1/2, p = 1,2,...,P(n) ,
wi ·
(Ti(bp,i) -
ci)2 )1/2, p = 1,2,...,P(n) ,
for target suitability, where ci denotes the
most or least preferred value of the i-th rank map.
The matrix product provides a concise, convenient expression for
the preceding two equations. For example, consider the following equation:
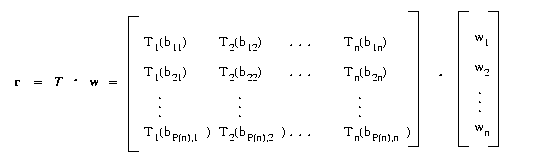
Likewise, given the ideal attributes I1 through In,
if t = (r12, r22,
... , rP(n)2), then the target attributes are given by:
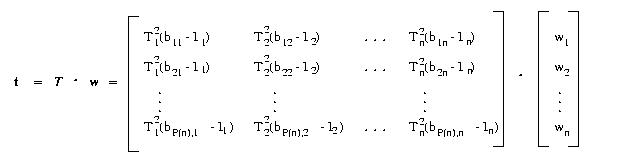
We next consider measures of geographic sensitivity. Given an expression for
Tn, the sensitivity of individual polygons can be determined.
At least five sensitivity measures for entire maps have been defined by
Lodwick [Lod94], as follows:
- Attribute Sensitivity Measures (ASMs) describe the net
magnitude of changes in attribute values from their unperturbed
values.
- Position Sensitivity Measures (PSMs) describe how many
of the attributes change with respect to their rank order from
their unperturbed (original or source) ranking.
- Map Removal Sensitivity Measures (MRSMs) describe how
the sensitivity associated with removing a set of maps from a
suitability analysis. This measure derives from perturbation of
the weight vector w that is equal in magnitude byt
opposite in sign to its value in the unperturbed suitability
analysis.
- Polygon Sensitivity Measures (PoSMs) determine which
polygons are more sensitive to perturbations.
- Areal Sensitivity Measures (ArSMs) compute the total
area over which attribute changes occur.
We examine each type of sensitivity measure, as follows.
1. Attribute Sensitivity Measures (ASMs):
Let rp denote the attirbute resulting from an absence of
perturbation, and let rp result from nonzero
perturbation. When sensitivity analysis does not require removal of
one or more maps from the suitability analysis, the weighted ASM is
given by:
m1(s,r,r) =
 sp
· | rp - rp | ,
sp
· | rp - rp | ,
where the weight vector s = (s1, s2, ... ,
sP(n)).
Notes:
· If sp = 1, then
m1 is said to be unweighted.
· If sp = Ap, where Ap denotes the
area of the p-th polygon, then m1 is said to be an
areal-weighted sensitivity measure.
· A normalized areal-weighted attribute sensitivity measure can
be computed by setting the p-th weight, as follows:
sp = Ap /  Ap .
Ap .
2. Position Sensitivity Measures (PSMs):
Let F denote the union of the attributes of n rank maps
denoted by rp 1  p
p
 P(n). Let
P(n). Let 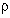 : F -> N denote the operation
that assigns rank order (e.g., from low to high) to all the attributes
of the P(n) polygons in the n overlaid suitability maps. The perturbed
attributes are denoted by rp.
: F -> N denote the operation
that assigns rank order (e.g., from low to high) to all the attributes
of the P(n) polygons in the n overlaid suitability maps. The perturbed
attributes are denoted by rp.
The weighted position sensitivity measure (e.g.,weighted for
position in a given rank ordering scheme) is given by:
m2(s,r,r) =
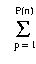 sp
· |
sp
· | 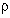 (rp) -
(rp) -
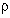 (rp) | ,
(rp) | ,
where the weight vector s = (s1, s2, ... ,
sP(n)) was defined previously.
Notes:
· If sp = 1,then m2 is said
to be unweighted.
· If sp = Ap, then
m2 is termed an areal-weighted rank sensitivity
measure.
· If sp portrays the proportion of total map
area occupied by the p-th polygon (per the preceding section on ASMs),
then m2 is said to be a normalized areal-weighted
rank sensitivity measure.
3. Map Removal Sensitivity Measures (MRSMs):
Removing one or more maps from a suitability analysis tends to lower
the perturbed attribute values rp for all polygons,
due to variance reduction. This removal represents a type of
analytical bias that can be compensated by dividing each suitability
map attribute by the number of primary maps n.
For example, if k denotes the number of primary maps remaining after
map removal, then the corresponding MRSM is given by:
m3(s,r,r) =
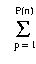 sp
· | (rp / n) - (rp / k) | ,
sp
· | (rp / n) - (rp / k) | ,
where the weight vector s was defined previously.
4. Polygon Sensitivity Measures (PoSMs):
To find which attributes undergo maximum change as a result of
perturbing the primary maps, one must find the polygon index or
indices for which | rp - rp | is
maximized.
The polygons that undergo maximum change have indices in the set
J = { (j 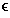 N :
| rj - rj | =
N :
| rj - rj | =
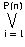 | ri - ri | } .
| ri - ri | } .
The polygon sensitivity measure is thus given by
m4(s,r,r) =
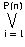 | ri - ri | .
| ri - ri | .
5. Area Sensitivity Measures (ArSMs):
The area that undergoes a change in attribute values given
perturbation of the primary maps is described by the following area
sensitivity measure:
m5(s,r,r) =
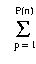 sp · Ap ,
sp · Ap ,
where sp = 1 if rp = rp or
sp = 0 otherwise.
Note: If sp = | rp - rp |,
then we obtain a relative area sensitivity measure.
Algorithm. The following procedure outlines the methodology
employed in computing geographic sensitivity analyses. Given a GIS
that can a) perform intersection overlay and b) access individual
attributes of n primary maps, perform the following steps:
Step 1. Obtain rp from perturbed inputs
by using r = T · w or t = T
· w, as given previously.
Step 2. Measure sensitivity using m1
through m5, as discussed in the preceding sections.
Step 3. If the probability distribution associated with
Monte Carlo simulation is known, then Monte Carlo simulation of
r = T · w or t = T ·
w would produce resultant attributes that could be analyzed
statistically.
4.2.3. Confidence Limits Associated with Geographic Sensitivity.
LEFT OFF HERE (middle of p.28 in notes)
4.2.3. Theory of Error Bounds in Discrete Algorithms
4.2.4. Software for Determining Error Bounds in Algorithms
4.2.5. Overview of Complexity Analysis for GIS Algorithms

4.3. Determining Elevation from Stereo Images in GIS Data
4.4. Integrating Surface Models with Elevation Data
References.
[Bib77] Bibby, J. "The general linear model: A cautionary
tale", in Analysis of Survey Data 2:35-80,
Eds. C. O'Muircheartaigh and C. Payne, New York: John Wiley (1977).
[Bis75] Bishop, Y., S. Fienberg, and P. Holland.
Discrete Multivariate Analysis: Theory and Practice, Boston,
MA: MIT Press (1975).
[Chr94] Chrisman, N.R. "Modelling error in overlaid
categorical maps", in Accuracy of Spatial Databases,
Eds. M. Goodchild and S. Gopal, London: Taylor and Francis, Second
Printing (1994).
[Goo78] Goodchild, M.F. "Statistical aspects of the polygon
overlay problem", Harvard Papers on Geographic Information Systems,
Volume 6, Reading, MA: Addison-Wesley (1978).
[McA71] McAlpine, J.R. and B.G. Cook. "Data reliability from
map overlay", in Proceedings of the 43rd Congress of the Australian
and New Zealand Association for the Advancement of Science (1971).
[Ver94] Veregin, H. "Error modeling for the map overlay
operation", in Accuracy of Spatial Databases, Eds. M. Goodchild
and S. Gopal, London: Taylor and Francis, Second Printing (1994).
This concludes our introductory discussion of GIS issues.
We next consider computational problems related to GIS features.
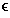 FX, where
1
FX, where
1  i
i
 n, let there be
ki polygons per layer. According to McAlpine and
Cook [McA71], an estimate of the number of spurious polygons
is given by:
n, let there be
ki polygons per layer. According to McAlpine and
Cook [McA71], an estimate of the number of spurious polygons
is given by: 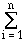 ki1/2 )2 .
ki1/2 )2 .


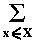 (aj(x) - bj(x))
(ai(x) - bi(x)) .
(aj(x) - bj(x))
(ai(x) - bi(x)) .
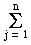 sij .
sij .
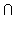 E2
E2
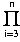 Pr[E1 |
Pr[E1 |
 (Ei)] ,
(Ei)] ,
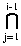 Ej .
Ej .




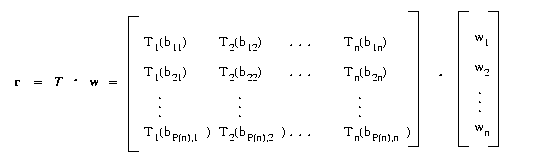
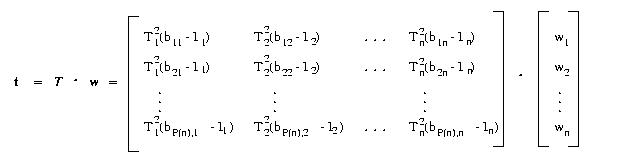
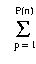 sp
· | rp - rp | ,
sp
· | rp - rp | ,
 : F -> N denote the operation
that assigns rank order (e.g., from low to high) to all the attributes
of the P(n) polygons in the n overlaid suitability maps. The perturbed
attributes are denoted by rp.
: F -> N denote the operation
that assigns rank order (e.g., from low to high) to all the attributes
of the P(n) polygons in the n overlaid suitability maps. The perturbed
attributes are denoted by rp. 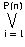 | ri - ri | } .
| ri - ri | } .
