Interact with smooth curves in OpenGL.

Place \(N=10\) control points to form a "figure 8" (see image; why are there only 9 points visible?).
Title the window "yourFirstname yourLastname (ufid)"
For each Task below show the control points and the curve
(sequence of line segments).
For Tasks 2 and 3 also the BB-polygon of coefficients
connected in red in the figure next to Task 3.
The points \(P_i\) are the same for all three Tasks.
The coefficients \(c_{i,j}\) in Task 2
are in general different from those in Task 3.
In Task 2, determine \(c_{i,0}\) and \(c_{i,3}\).
In Task 3, determine \(c_{i,1}\) and \(c_{i,2}\).
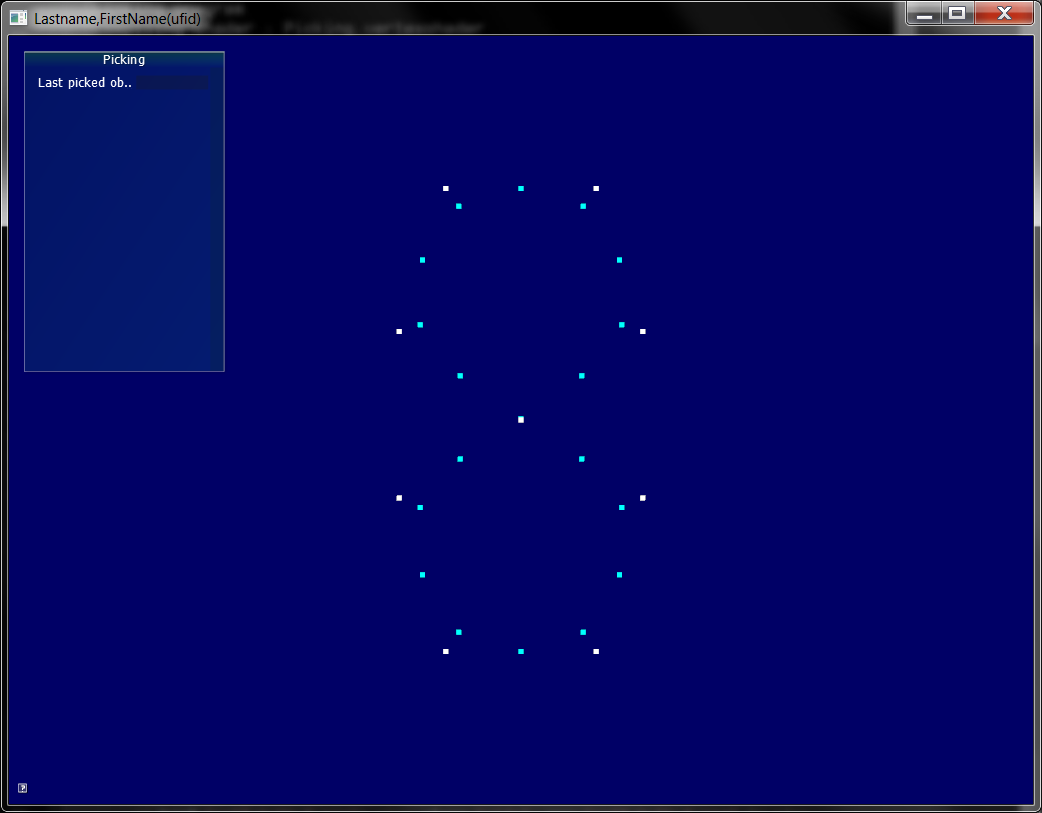
Initialize \(P_i^0 = P_i\) (white points).
Use these formulas to create a refined set of control points (cyan)
where
\(i\) is the index of points is in range \(0 \dots (N\times 2^k-1)\) .
The figure illustrates one step of subdivision.
Your implementation should allow repeated refinement (at least 5 times).
Upon pressing key 1, one additional refinement should be triggered.
Initially when (\(k=0\)), the control polygon should be drawn without subdivision.
Whenever key
1 is pressed the subdivided control polygon should be redrawn.
Every sixth refinement resets to level \(k=0\).

Let \(\mathbf{P}=\{P_1,\dots,P_N\}\) be the the set of input points.
You will construct \(N\) Bézier curves of degree 3:
one curve segment for each input point.
The coefficients of the ith curve are
\(\mathbf{c}_i=\{c_{i,0},c_{i,1},c_{i,2},c_{i,3}\}\).
The interior Bézier points (yellow) are:
Determine \(c_{i,0}\) and \(c_{i,3} = c_{i+1,0}\) so that
the polynomial pieces join \(C^1\).
Write down the formulas for \(c_{i,0}\) and \(c_{i,3}\)
and place them into your ReadMe.txt file.
This method should be activated when key 2 is pressed on the keyboard

Let \(\mathbf{P}=\{P_1,\dots,P_N\}\) be the the set of input points.
Construct a Catmull-Rom curve that interpolates the \(N\) points \(P_i\) as follows.
There are \(N\) Bézier curve segments of degree 3.
The coefficients of each segment \(i\) are \(\mathbf{c}_i=\{c_{i,0},c_{i,1},c_{i,2},c_{i,3}\}\)
where \(c_{i,0} = P_{i}\) and \(c_{i,3} = P_{i+1}\).
The tangent at \(c_{i,0}\) is a multiple of \(P_{i+1}-P_{i-1}\).
Once all of the Bézier points (red) are determined use deCasteljau's Algorithm
to evaluate the curve at 17 points per segment.
Connecting the points yields the Catmull-Rom curve (green).
This method should be activated when key 3 is pressed on the keyboard
Implement Task 3 using the OpenGL 4.x's tessellation engine.

Make sure picking still works on the original \(N\) vertices, and your curves adapt to their movement.