Reconstruction Gallery

‘Marschner-Lobb’ test function [1]

ρ(x,y,z)=	1-sin(πz/2)+α(1+ρr((x2+y2)½))
	2(1+α)

where

• ρ_r(r)= cos(2πf_Mcos(πr/2))
• f_M=6
• α=0.25

Level set 0.5 is rendered.

	C¹ on FCC	C² on BCC	C¹ on Cartesian	C² on Cartesian
filter	6-dir. box spline	8-dir. box spline [2][3]	tri-quadratic B-spline	tri-cubic B-spline
degree of filter	3	5	6	9
approx. order	3	4	3	4
stencil size	16	32	3³=27	4³=64

density	C¹ on FCC	C² on BCC	C¹ on Cartesian	C² on Cartesian
(0.03)-3
(0.05)-3
(0.06)-3
(0.07)-3
(0.08)-3
(0.09)-3

density	C¹ on FCC	C² on BCC	C¹ on Cartesian	C² on Cartesian
(0.05)-3
(0.06)-3
(0.07)-3
(0.08)-3
(0.09)-3

density	C¹ on FCC	C² on BCC
(0.07)-3

density	FCC|BCC	FCC|BCC
(0.05)-3
(0.06)-3
(0.07)-3
(0.08)-3
(0.09)-3

density	C¹ on FCC	C² on BCC
(0.05)-3
(0.06)-3
(0.07)-3
(0.08)-3
(0.09)-3

density	C¹ on FCC	C² on BCC
(0.05)-3
(0.06)-3
(0.07)-3
(0.08)-3
(0.09)-3

Carp dataset

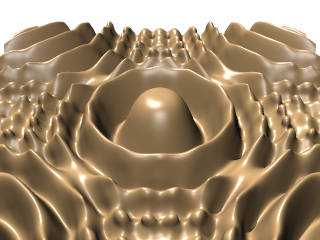
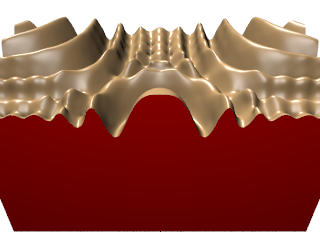
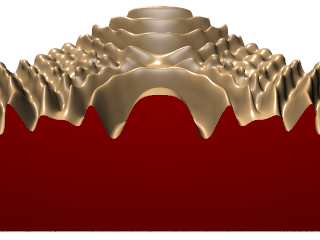
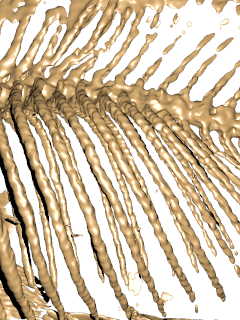
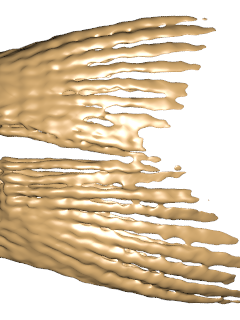
↓ C¹ on Cartesian (256×256×512, density=1)

lattice units = (0.78125,0.390625,1)

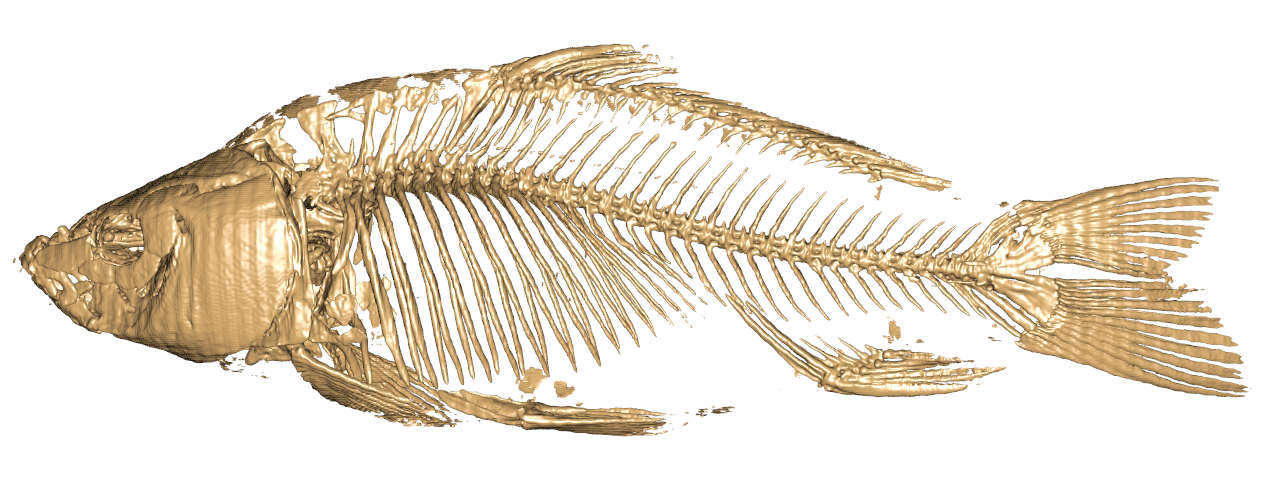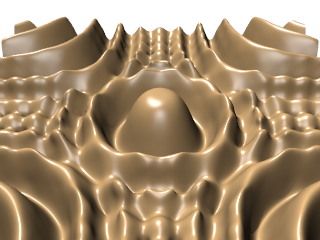
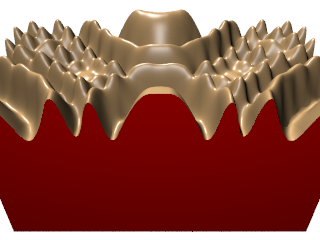
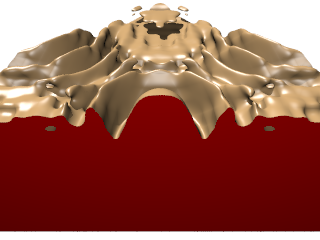
↓ C¹ on Cartesian (100×100×200, density=1/(256/100)³=0.0596)

lattice units = ×(256/100)

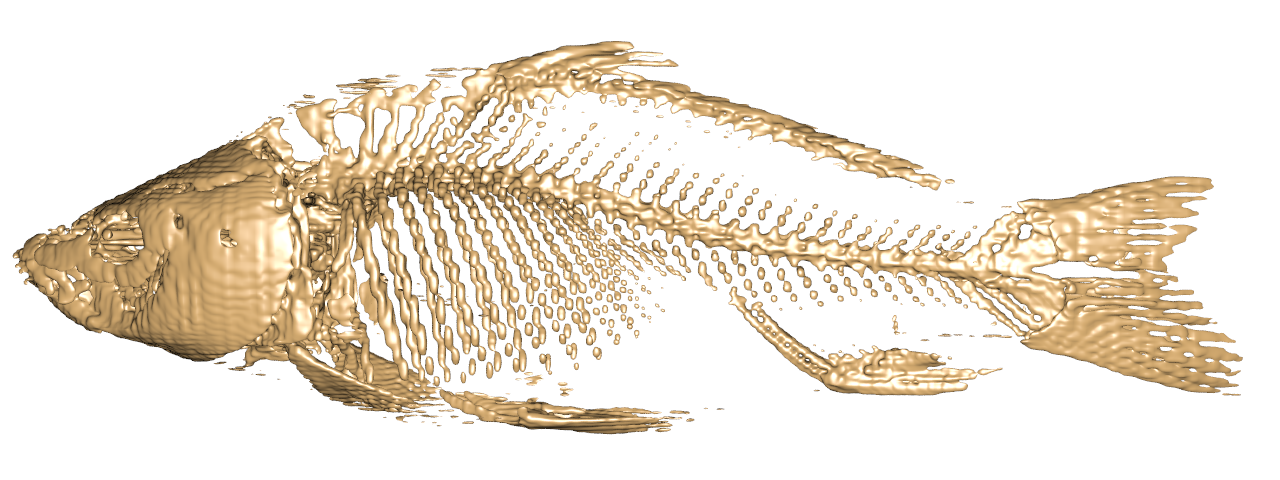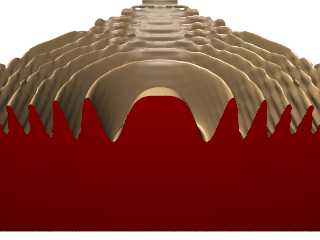
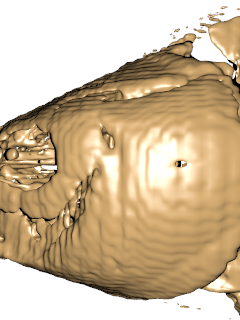
↓ C¹ on FCC (63×63×126×4, density=4/(2*(256/126))³=0.0596)

lattice units = ×(256/126)

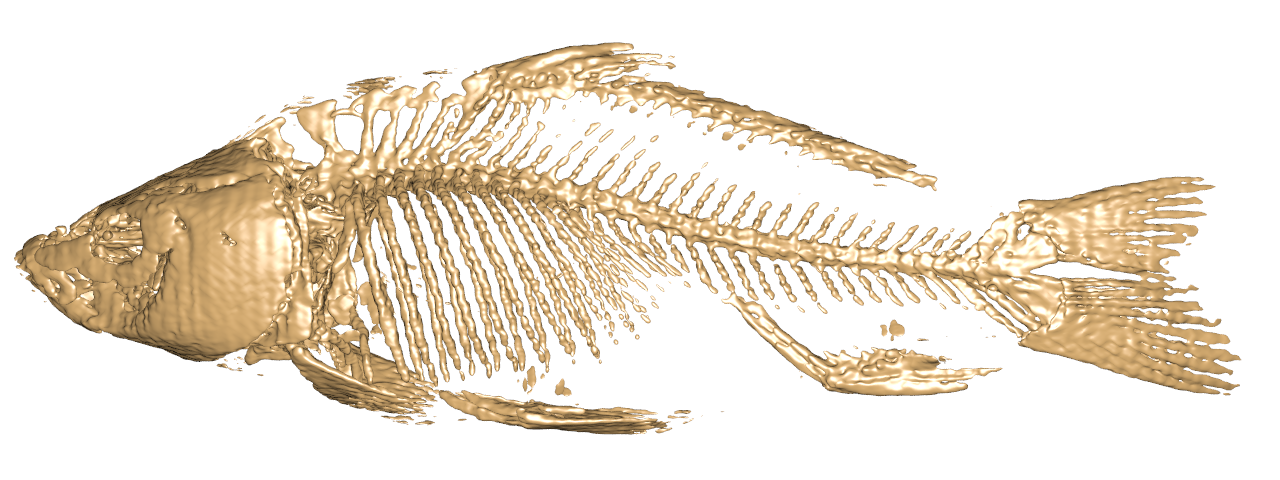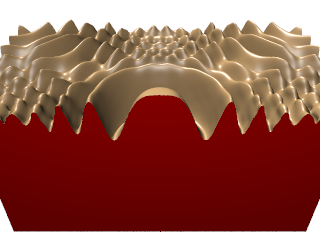
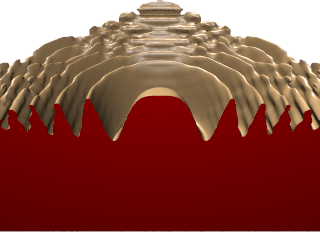
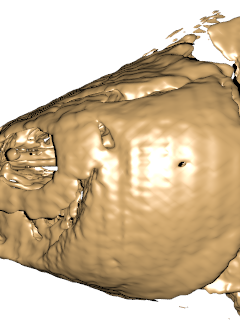
↓ C¹ on Cartesian (cut in half, 100×100×200, density=1/(256/100)³=0.0596)

lattice units = ×(256/100)

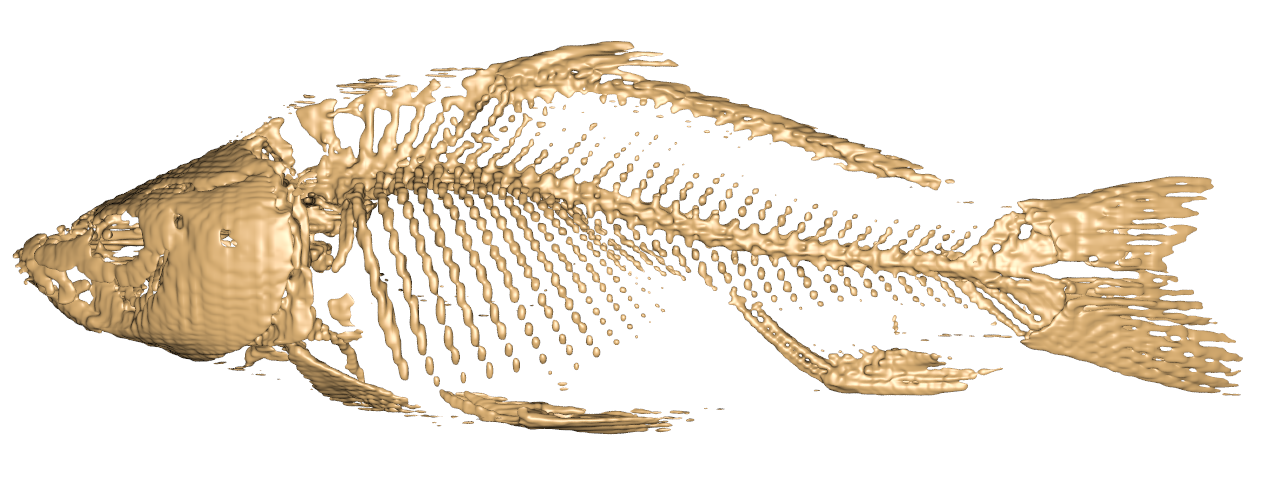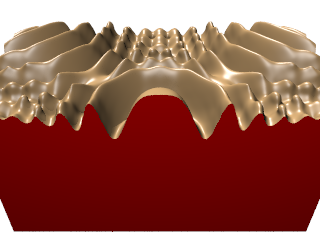
↓ C¹ on FCC (cut in half, 63×63×126×4, density=4/(2*(256/126))³=0.0596)

lattice units = ×(256/126)

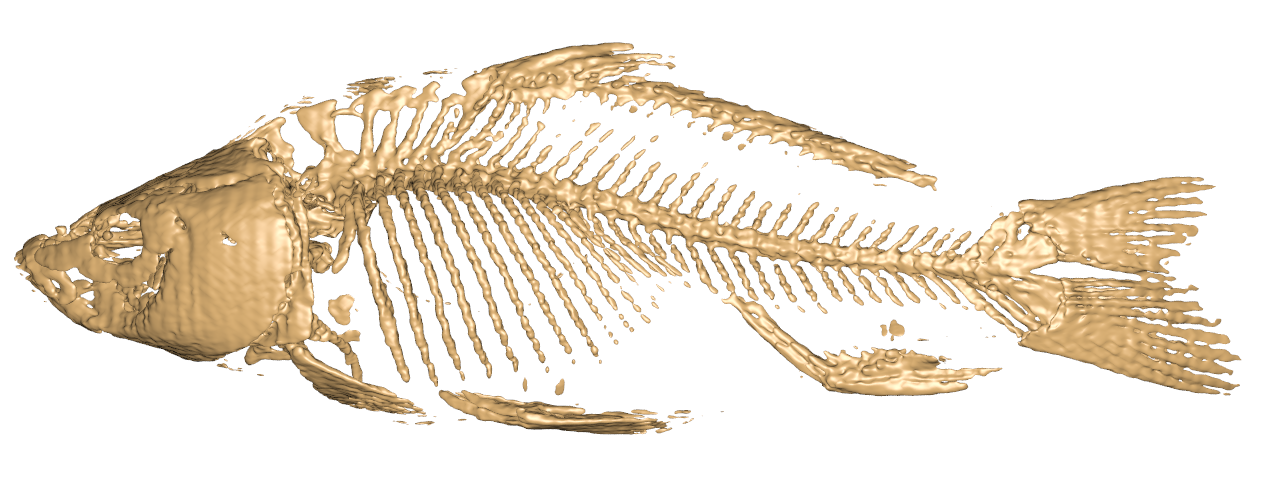↓ C¹ on Cartesian (120×120×242, density=1/(256/120)³=0.1030)

lattice units = ×(256/120)

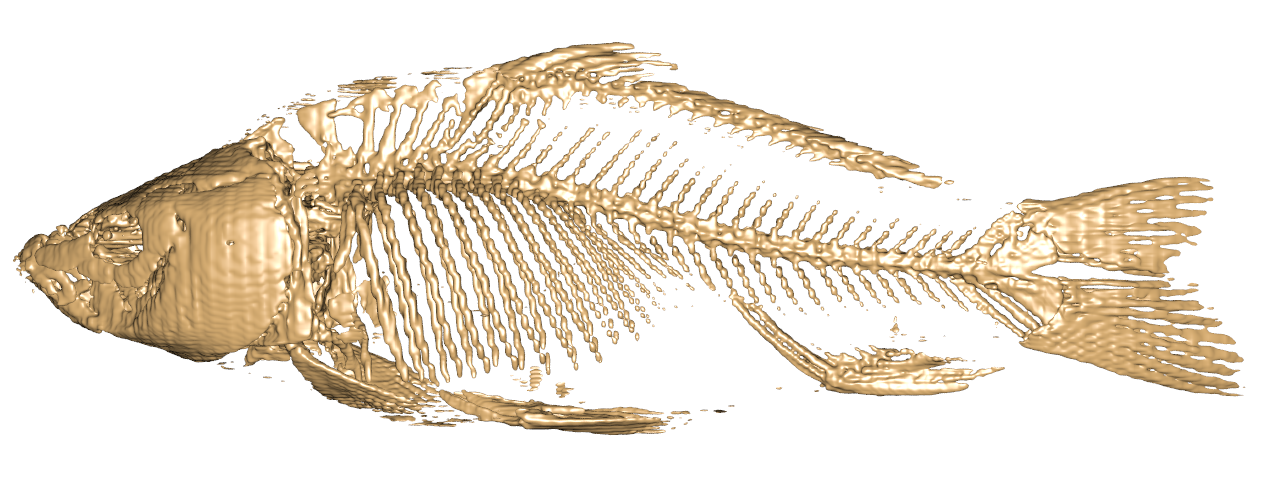↓ C¹ on FCC (75×75×150×4, density=4/(2*(256/150))³=0.1006)

lattice units = ×(256/150)

C¹ on Cartesian	C¹ on FCC
120×120×242	75×75×150×4
0.1016	0.0998

References

1. Stephen R. Marschner and Richard J. Lobb, “An Evaluation of Reconstruction Filters for Volume Rendering”, In Proceedings of Visualization '94, pages 100-107. Held in Washington, DC, October 1994.
2. Alireza Entezari and Ramsay Dyer and Torsten Möller, “Linear and Cubic Box Splines for the Body Centered Cubic Lattice”, pages 11-18, In Proceedings of the IEEE Conference on Visualization, October 2004.
3. Alireza Entezari, “Optimal Sampling Lattices and Trivariate Box Splines” (Ph.D thesis), Simon Fraser University, Vancouver, Canada, July 2007.
4. The Volume Library @University of Erlangen