Data Structures, Algorithms, & Applications in Java
Pairing Heaps
Copyright 1999 Sartaj Sahni
Introduction
Definition and Operations
isEmpty, size, and getMax
meld (compare-link)
put
increaseKey
removeMax
remove
Implementation Considerations
Complexity and an Enhancement
Introduction
In the text, we studied two data structures--heaps
and leftist trees--for the representation of a
priority queue.
When a max heap is used to represent a max priority queue, the
put and removeMax
operations take O(log n) time,
where n is the number of elements in the
priority queue. The remaining priority queue
operations--isEmpty, size,
and getMax--take O(1) time
each. Leftist trees provide the same asymptotic complexity as do heaps.
Additionally, when a leftist tree is used, two priority queues can be melded
in O(log n) time.
In many applications, we are concerned more with the time it takes to perform
a sequence of priority queue operations than we are with the time it takes
to perform an individual operation. For example, when
we sort using the heap sort method, we are concerned with the time
it takes to complete the entire sort; not with the
time it takes to remove the next element from the max heap.
In these applications, it is adequate to use a data structure that
has a good amortized complexity
for each operation type.
Fibonacci heaps and pairing heaps are two of the more popular
priority queue data structures for which the amortized complexity of
priority queue operations is good.
When a max Fibonacci heap is used, the actual and amortized
complexities of various operations on an n element
priority queue are
Operation Actual Complexity Amortized Complexity
isEmpty O(1) O(1)
size O(1) O(1)
getMax O(1) O(1)
put O(1) O(1)
removeMax O(n) O(log n)
meld O(1) O(1)
remove O(n) O(log n)
increaseKey O(n) O(1)
The operation remove(theNode) removes from the
data structure an arbitrary node theNode,
and the operation increaseKey(newValue, theNode)
replaces the key (i.e., the priority)
in the node theNode by a larger
value newValue (for a min priority queue, the
corresponding operation decreaseKey(newValue, theNode)
replaces the key in the node theNode by a smaller
value newValue).
When an auxiliary two pass max pairing heap is used,
the actual and amortized complexities for the above operations
are as below.
Operation Actual Complexity Amortized Complexity
isEmpty O(1) O(1)
size O(1) O(1)
getMax O(1) O(1)
put O(1) O(log n)
removeMax O(n) O(log n)
meld O(1) O(log n)
remove O(n) O(log n)
increaseKey O(1) O(log n)
Although the amortized complexities given above are not known to be
tight (i.e., no one knows of an operation sequence whose
run time actually grows logarithmically with the number of
increase key operations (say)), it is known that
the amortized complexity of the increase key operation
is Omega(log log n). The papers
On the efficiency of pairing heaps and related data
structures, by M. Fredman
and
Information theoretic implications for pairing heaps,
by M. Fredman,
ACM Symposium on the Theory of Computing, 1998 provide an information theoretic
proof of this lower bound on the amortized complexity of the
increase key operation for pairing heaps.
Experimental studies indicate that pairing heaps actually outperform
Fibonacci heaps. Therefore, we develop pairing heaps only.
Definition and Operations
Pairing heaps come in two varieties--min pairing heaps and max pairing heaps.
Min pairing heaps are used when we wish to represent a min priority queue,
and max pairing heaps are used for max priority queues. In keeping with our
discussion of heaps and leftist trees in the text, we explicitly discuss
max pairing heaps here. Min pairing heaps are analogous.
A max pairing heap is simply a max tree (see Definition 9.1 of the text)
in which the operations are performed in a manner to be specified later.
Four max pairing heaps are shown below.
Notice that a pairing heap need not be a binary tree.
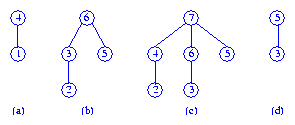
isEmpty, size, and getMax
In a pairing heap, the isEmpty and
size operations are done
by maintaining a variable size which gives the
number of elements currently in the data structure.
Since the max element is in the root of the max tree, the
getMax operation is done
by returning the element in the root.
meld (compare-link)
Two max pairing heaps may be melded into a single max pairing heap
by performing a compare-link operation.
In a compare-link, the roots of the two max trees are compared and the
max tree that has the smaller root is made the leftmost subtree of the
other tree (ties are broken arbitrarily).
To meld the max trees (a) and (b), above, we compare the two roots.
Since tree (a) has the smaller root, this tree becomes the leftmost subtree
of tree (b). The resulting tree, tree (e), is shown below.
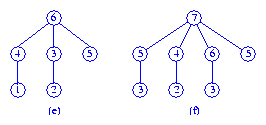
Tree (f) is the result of melding the trees (c) and (d).
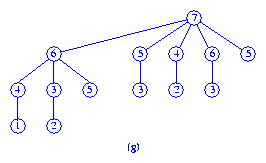
When we meld the trees (e) and (f), the result is the tree (g).
put
To put an element theElement
into a pairing heap p, we first create a pairing heap
q
with the single element theElement, and then meld
the two pairing heaps p and q.
increaseKey
Suppose we increase the key of the element in node theNode.
When theNode is the root or when the new key in
theNode is less than or equal to that in its parent,
no additional work is to be done. However, when the new key in
theNode is greater than that in its parent,
the max tree property is violated and corrective action is to be taken.
For example, if the key in the root of tree (c) is increased from
7 to 10, or
when the key in the leftmost child of the root of tree (c) is increased from
4 to 6 no additional work
is necessary. However,
when the key in the leftmost child of the root of tree (c) is increased from
4 to 9 the new value is larger
than that in the root (see tree (h)) and corrective action is needed.
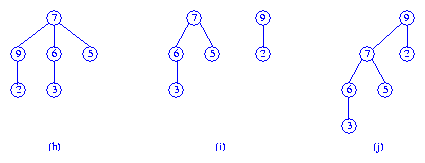
Since pairing heaps are normally not implemented with a parent pointer,
it is difficult to determine whether or not corrective action is needed
following the key increase. Therefore, corrective action is taken regardless
of whether or not it is needed except when theNode
is the tree root. The corrective action consists of the following steps:
-
Remove the subtree with root
theNode from the
tree. This results in two max trees.
-
Meld the two max trees together.
Figure (i) shows the two max trees following step 1, and tree (j)
is the result of step 2.
removeMax
The max element is in the root of the tree. When the root is removed,
we are left with zero or more max trees (i.e., the subtrees of
the removed root). In two pass pairing heaps, these
max trees are melded into a single max tree as follows:
-
Make a left to right pass over the trees, melding pairs of trees.
-
Start with the rightmost tree and meld the remaining trees (right to left)
into this tree
one at a time.
Consider the max tree (k). When the root is removed, we get the
collection of 6 max trees shown in Figure (l).
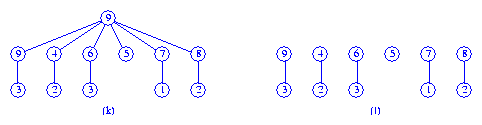
In the left to right pass, we first meld the trees with roots
9 and 4.
Next, the trees with roots
6 and 5 are melded.
Finally,
the trees with roots
7 and 8 are melded.
The three max trees that result are shown in Figure (m).
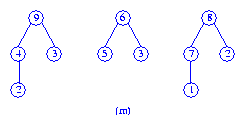
In the second pass (which is a right to left pass), the two rightmost trees
of Figure (m) are first melded to get the tree of Figure (n).
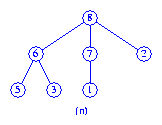
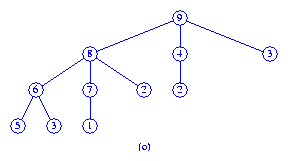
Then the tree of Figure (m) with root 9
is melded with the tree of Figure (n) to get the final max tree
which is shown in Figure (o).
Note that if the original pairing heap had 8
subtrees, then following the left to right melding pass we would be left
with 4 max trees. In the right to left pass,
we would first meld trees 3 and 4
to get tree 5. Then trees
2 and 5 would be melded
to get tree 6. Finally, we would meld
trees 1 and 6.
In multi pass pairing heaps, the max trees that remain following
the removal of the root
are melded into a single max tree as follows:
-
Put the max trees onto a FIFO queue.
-
Extract two trees from the front of the queue,
meld them and put the resulting tree at the end of the queue.
Repeat this step until only one tree remains.
Consider the six trees of Figure (l) that result when the root of tree (k)
is removed.
First, we meld the trees with roots
9 and 4 and put the resulting
max tree at the end of the queue.
Next, the tree with roots
6 and 5 are melded and
the resulting
max tree is put at the end of the queue.
And then, the tree with roots
7 and 8 are melded and the
resulting max tree added to the queue end.
The queue now contains the three max trees shown in Figure (m).
Next, the max trees with roots
9 and 6 are melded and the
result put at the end of the queue.
We are now left with the two max trees shown in Figure (p).
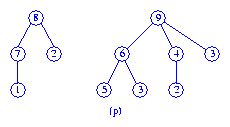
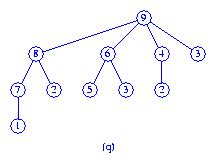
Finally, the two max trees of Figure (p) are melded to get the max tree of
Figure (q).
remove
The operation remove(theNode) is handled
as a removeMax operation when
theNode is the root of the pairing heap.
When theNode is not the tree root, the
remove operation is done as follows:
-
Detach
the subtree with root
theNode from the tree.
-
Remove the node
theNode and meld its subtrees
into a single max tree using the two pass scheme if we are implementing
a two pass pairing heap or the multi pass scheme if we are implementing a
multi pass pairing heap.
-
Meld the max trees from steps 1 and 2 into a single max tree.
Implementation Considerations
Although we can implement a pairing heap using nodes that have a variable
number of children fields, such an implementation is expensive because
of the need to dynamically increase the number of children fields as needed.
An efficient implementation is possible by using the binary tree representation
of a tree (see Figure 12.15 of the text).
Siblings in the original max tree
are linked together using a doubly linked list.
Each node has the three pointer fields previous,
next, and
child.
The leftmost
node in a doubly linked list of siblings uses its
previous
pointer to point to its parent. A leftmost child satisfies the property
x.previous.child = x.
The doubly linked list makes it is possible
to remove an arbitrary element (as is required by the
remove and increaseKey
operations) in O(1) time.
Complexity and an Enhancement
You can verify that using the described binary tree representation,
all pairing heap operations (other than removeMax
and remove) can be done in O(1)
time. The complexity of the
removeMax
and remove operations is O(n),
because the number of subtrees that have to be combined following
the removal of a node is O(n).
The paper The pairing heap: A new form of self-adjusting heap,
Algorithmica,
1, March 1986, 111-129,
by M. Fredman, R. Sedgewick, R. Sleator, and R. Tarjan,
shows that the amortized complexity of the put,
meld,
removeMax,
remove,
and increaseKey operations is O(log n),
and that of the remaining operations is O(1).
Experimental studies conducted by Stasko and Vitter reported in their paper
Pairing heaps: Experiments and analysis, Communications of the ACM,
30, 3, 1987, 234-249 establish the
superiority of two pass pairing heaps
over
multipass pairing heaps.
The above paper by Stasko and Vitter also proposes a variant
of pairing heaps
(called auxiliary two pass pairing heaps)
that performs better than two pass pairing heaps.
In an auxiliary two pass pairing heap we maintain a main max tree
mainTree, an
auxiliary list auxList of max trees, and a pointer
maxElement to the max tree that has the
largest root. Initially,
the tree mainTree, the list
auxList, and the pointer
maxElement are all null.
The isEmpty,
size, and
getMax operations are performed exactly as they are
in an ordinary two pass pairing heap.
A put is done by adding a single-node max tree to
the end of the list auxList and updating the pointer
maxElement if necessary.
An increaseKey(newValue, theNode) is done by detaching
the tree with root theNode from its parent,
changing the key in theNode to
theValue, updating maxElement
if necessary, and adding the tree with root theNode
to the end of the list auxList.
The removeMax operation of an auxiliary two pass
pairing heap is done as follows:
-
Meld the max trees in
auxList using the multi pass
scheme. That is, put the trees in auxList onto a
FIFO queue and pairwise meld from the front of this queue until only one tree
remains in the queue. Note that the result of each meld is added to the
end of the queue.
-
Meld the main tree and the tree that results from the pairwise melding of
Step 1.
-
The root of the single max tree that remains is the max element.
This root is removed and the subtrees are melded into a single max tree
using the two pass scheme.
The steps for the remove(theNode) operation are:
-
If
theNode = maxElement, then a
removeMax (as described above for the auxiliary
two pass pairing heap) is done.
-
If
theNode is the root of a max tree
T, then a
removeMax (as described for a two pass pairing heap)
is done on T.
-
Otherwise,
- (a)
-
Detach
the subtree with root
theNode from its tree
U.
- (b)
-
Remove the node
theNode and meld its subtrees
into a single max tree using the two pass scheme.
- (c)
-
Meld the max trees from steps (a) and (b) into a single max tree.
- (d)
-
Leave the resulting tree in
auxList if the tree
U was initially there.
To meld two auxiliary two pass pairing heaps, we do the following
-
Concatenate the auxialiary lists of the two pairing heaps.
-
Add one of the two main trees to the end of the auxiliary list created
in step 1.
-
The other main tree becomes the main tree for the result.
-
maxElement for the result is the larger of the
max elements of the two pairing heaps being melded.
Although an auxiliary multi pass pairing heap is also defined by
Stasko and Vitter, this version performs worse than the basic
multi pass pairing heap.










