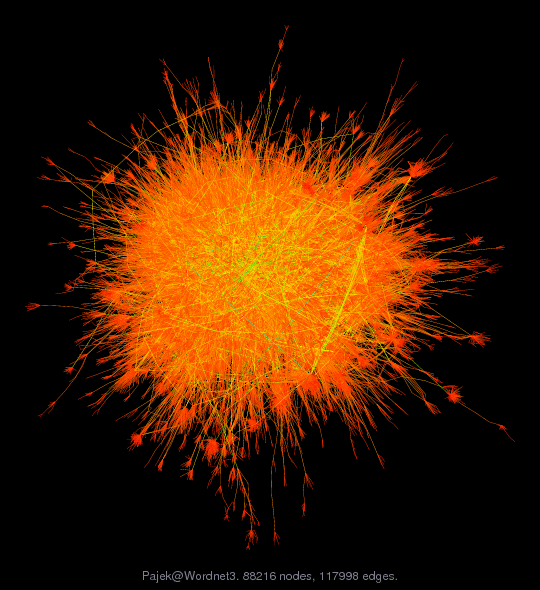
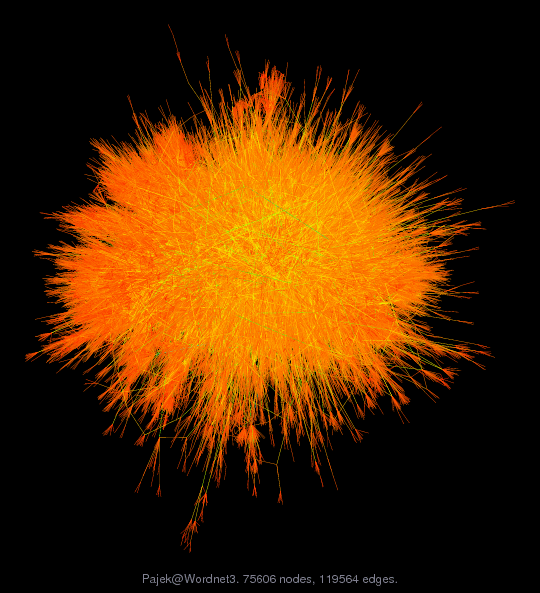
Matrix: Pajek/Wordnet3
Description: Pajek network: Wordnet3 dictionary network
 |
 |
| (bipartite graph drawing) | (graph drawing of A+A') |
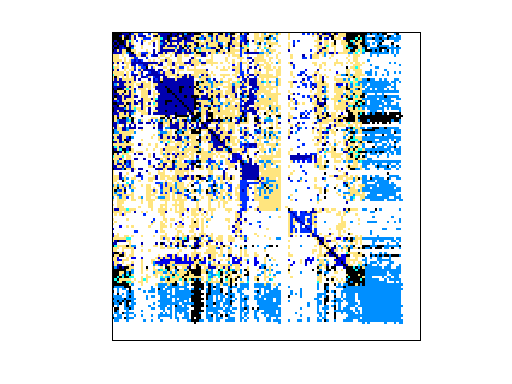 |
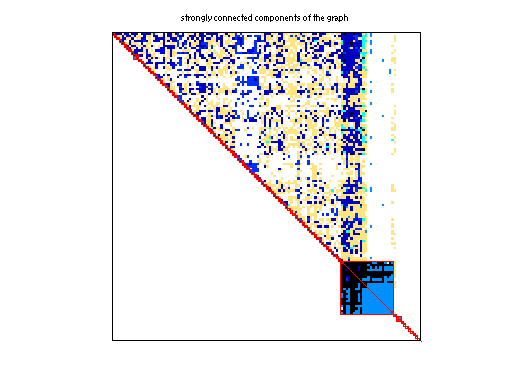 |
| Matrix properties | |
| number of rows | 82,670 |
| number of columns | 82,670 |
| nonzeros | 132,964 |
| # strongly connected comp. | 67,689 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | 18% |
| numeric value symmetry | 17% |
| type | integer |
| structure | unsymmetric |
| Cholesky candidate? | no |
| positive definite? | no |
| author | |
| editor | V. Batagelj |
| date | 2006 |
| kind | directed weighted graph |
| 2D/3D problem? | no |
| Additional fields | size and type |
| edgecode | full 9-by-28 |
| nodecode | full 5-by-4 |
| category | full 82670-by-1 |
| nodename | full 82670-by-69 |
Notes:
------------------------------------------------------------------------------ Pajek network converted to sparse adjacency matrix for inclusion in UF sparse matrix collection, Tim Davis. For Pajek datasets, See V. Batagelj & A. Mrvar, http://vlado.fmf.uni-lj.si/pub/networks/data/. ------------------------------------------------------------------------------ NOTE: this is a binary graph in the Pajek dataset, but where each edge has a label (not a weight) in the range 1 to 9. The following labels are used: 1 hypernym pointer 2 entailment pointer 3 similar pointer 4 member meronym pointer 5 substance meronym pointer 6 part meronym pointer 7 cause pointer 8 grouped pointer 9 attribute pointer This is not a multigraph. There are no edges (i,j) between the same nodes with the same label. Thus, in the sparse matrix, the edge weight A(i,j) represents the label 1 through 9 of edge (i,j). No loss of information occurs in this translation. The above table is in aux.edgecode(1:9,:). Each node is a word in a dictionary. aux.category(i) gives the category of the word: 1: n (noun?) 63099 words 3: a (adjective?) 5501 words 4: r (?) 2846 words 5: s (?) 6728 words. ------------------------------------------------------------------------------
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.