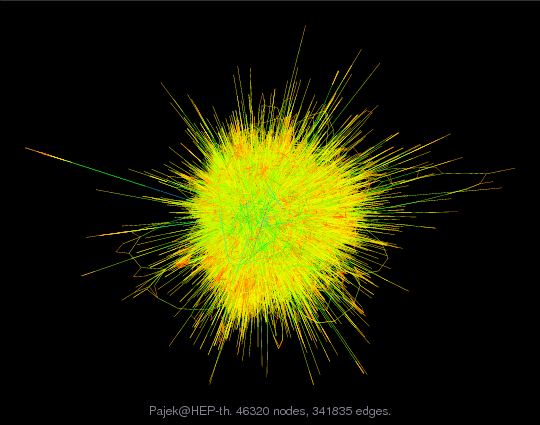
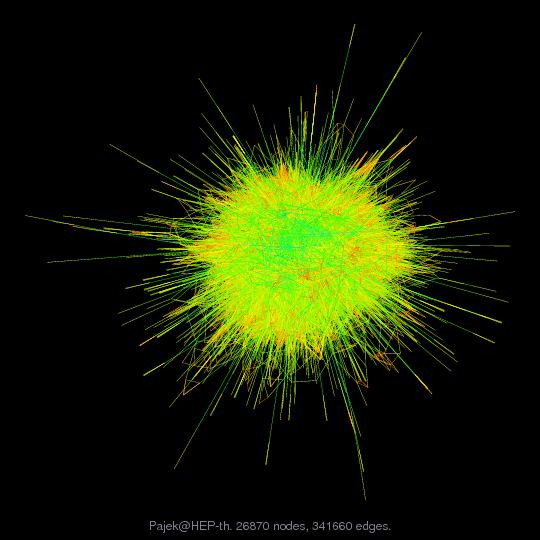
Matrix: Pajek/HEP-th
Description: Pajek network: High Energy Physics literature
 |
 |
| (bipartite graph drawing) | (graph drawing of A+A') |
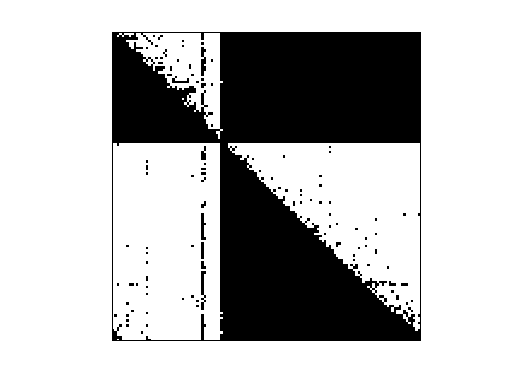 |
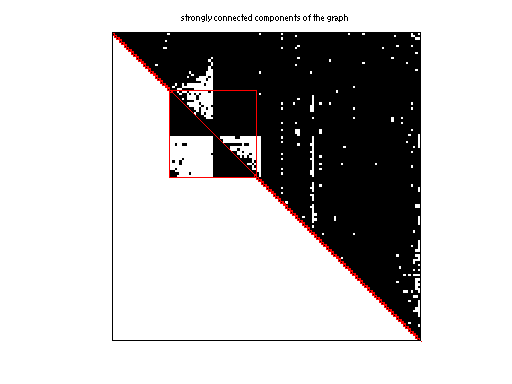 |
| Matrix properties | |
| number of rows | 27,240 |
| number of columns | 27,240 |
| nonzeros | 342,437 |
| # strongly connected comp. | 19,565 |
| explicit zero entries | 0 |
| nonzero pattern symmetry | 0% |
| numeric value symmetry | 0% |
| type | binary |
| structure | unsymmetric |
| Cholesky candidate? | no |
| positive definite? | no |
| author | KDD Cup 2003 |
| editor | V. Batagelj |
| date | 2003 |
| kind | directed graph |
| 2D/3D problem? | no |
| Additional fields | size and type |
| nodename | full 27240-by-7 |
Notes:
------------------------------------------------------------------------------
Pajek network converted to sparse adjacency matrix for inclusion in UF sparse
matrix collection, Tim Davis. For Pajek datasets, See V. Batagelj & A. Mrvar,
http://vlado.fmf.uni-lj.si/pub/networks/data/.
------------------------------------------------------------------------------
High Energy Particle Physics (HEP) literature
---------------------------------------------
Citation data from KDD Cup 2003, a knowledge discovery and data mining
competition held in conjunction with the Ninth Annual ACM SIGKDD Conference.
http://www.cs.cornell.edu/projects/kddcup/index.html
The Stanford Linear Accelerator Center SPIRES-HEP database has been
comprehensively cataloguing the High Energy Particle Physics (HEP) literature
online since 1974, and indexes more than 500,000 high-energy physics related
articles including their full citation tree.
The network contains a citation graph of the hep-th portion of the arXiv.
The units names are the arXiv IDs of papers; the relation is X cites Y .
Note that revised papers may have updated citations. As such, citations may
refer to future papers, i.e. a paper may cite another paper that was publishe
after the first paper.
Update May 12, 2003 is not included.
transformed in Pajek format: V. Batagelj, 26. July 2003
-----
| SVD-based statistics: | |
| norm(A) | 84.3235 |
| min(svd(A)) | 5.59609e-66 |
| cond(A) | 1.50683e+67 |
| rank(A) | 21,162 |
| null space dimension | 6,078 |
| full numerical rank? | no |
| singular value gap | 1.3948e+08 |
| singular values (MAT file): | click here |
| SVD method used: | s = svd (full (A)) |
| status: | ok |
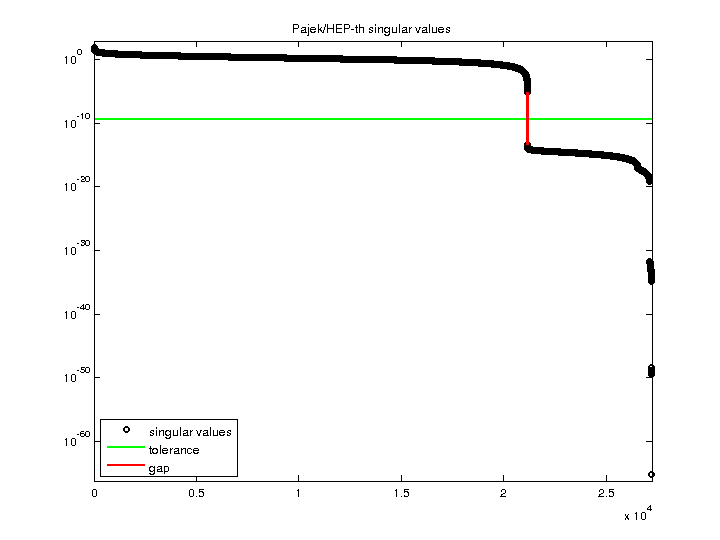
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.